【8】平衡树学习笔记
前言
我的平衡树学得不是很好,旋转那一部分弄得不是很清楚。并且学的平衡树也没有那么多种,只有自己通用的平衡树 Splay 和小常数平衡树 Treap,刚好是两个基于旋转的平衡树。这篇学习笔记主要用于巩固平衡树知识,并为 LCT 学习笔记最好准备。
长文警告:本文一共 \(1757\) 行,请合理安排阅读时间。
UPD on \(2025.8.3\):添加了 FHQ-Treap,FHQ-Treap 真香!
前置知识:【6】线段树学习笔记
二叉搜索树
在本博客中,平衡树中节点 \(x\) 的左儿子记作 \(ch[x][0]\),右儿子记作 \(ch[x][1]\),父节点记作 \(fa[x]\),权值记作 \(a[x]\)。
二叉搜索树是一棵二叉树,这棵二叉树的每一个节点 \(x\) 满足以下条件:
\(1\):若 \(ch[x][0]\) 不为空,则其左子树内所有节点 \(i\) 满足 \(a[i]\lt a[x]\)。
\(2\):若 \(ch[x][1]\) 不为空,则其右子树内所有节点 \(i\) 满足 \(a[i]\gt a[x]\)。
不难发现,一棵二叉搜索树的左右子树均为二叉搜索树。
注意到二叉搜索树每次操作的时间复杂度为 \(O(h)\),其中 \(h\) 为树高。注意到极端数据可以使树退化成链,\(h\) 可以达到 \(n\) 的级别。因此,二叉搜索树每次操作的时间复杂度为 \(O(n)\),非常不优秀。
Treap
注意到同一棵二叉搜索树可以有不同的形态。例如,下面两张图片都是依次插入 \(1,3,4,5,9,10,16,18\) 的二叉搜索树。
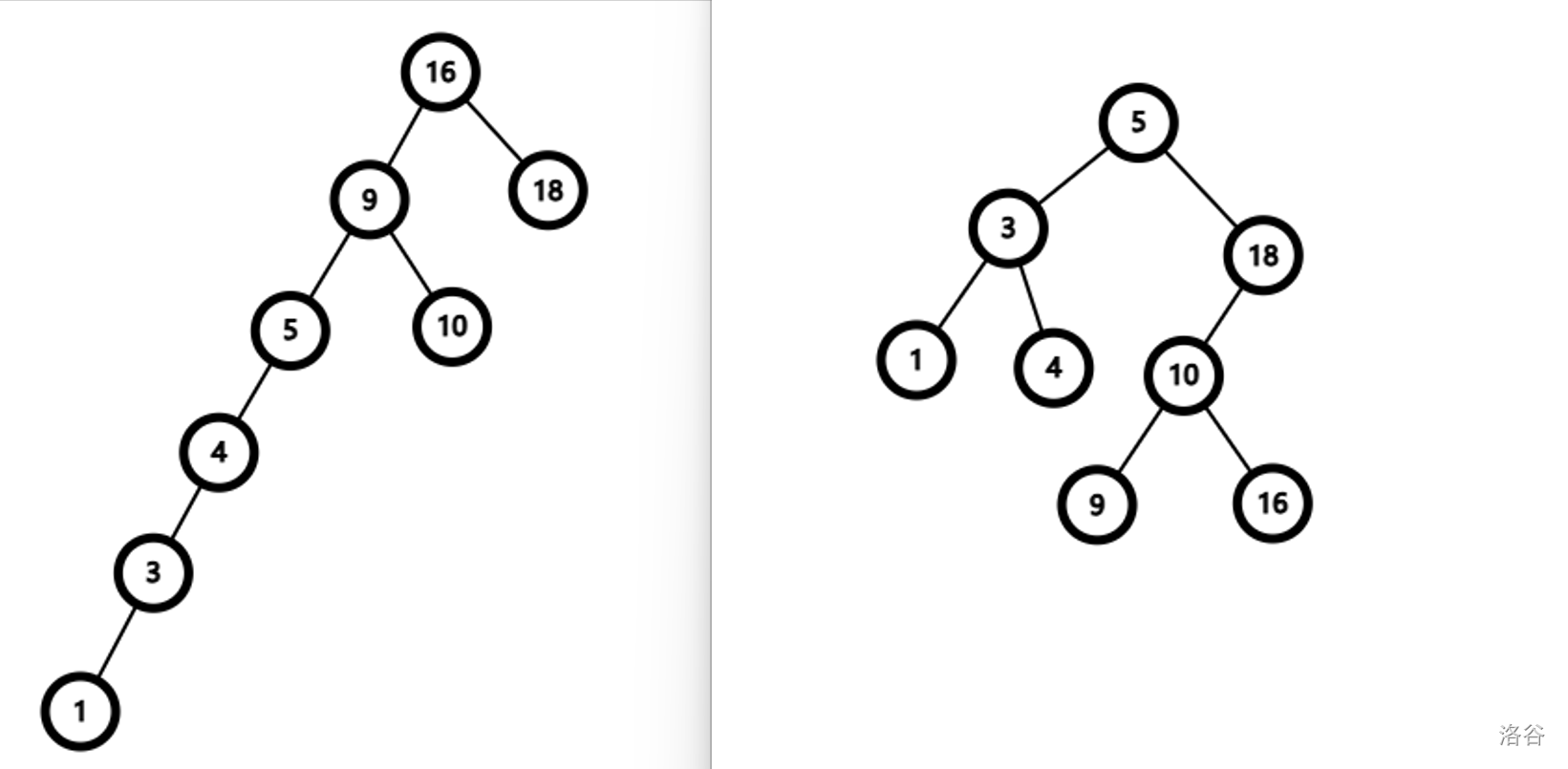
显然,右边的树比左边的树深度更小。我们称这样的树更平衡。注意到二叉树的深度可以达到 \(O(\log n)\) 级别,如果我们把树尽量平衡,每次操作的时间复杂度可以达到 \(O(\log n)\) 级别,较为优秀。
为了使这棵树更加平衡,我们引入旋转操作。旋转操作的定义为在不破坏二叉搜索树性质的情况下,修改树中的节点的父子关系。
记当前旋转节点为 \(x\),其父亲为 \(y\),爷爷为 \(z\)。由于旋转时需要确定方向,所以我们需要知道一个节点是其父亲的左儿子还是右儿子。这个过程可以单独写一个函数。
bool wh(int x)
{
return ch[fa[x]][1]==x;
}
若为左儿子,返回 \(0\);若为右儿子,返回 \(1\),恰好对应定义中的编号。
我们把图画出来,考虑旋转时节点关系的变化。
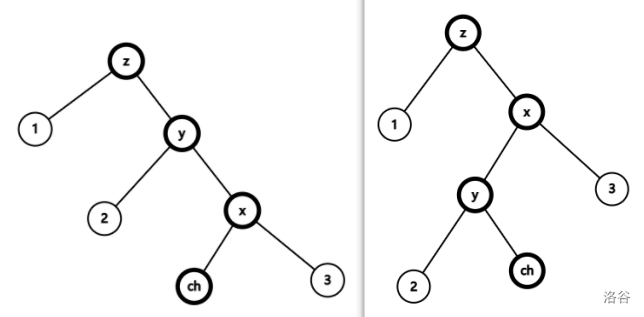
我们发现,在一次旋转中,只有图中加粗节点部分与其他节点的关系发生了变化。具体的,我们把每个点的变化写出来。其中 \(wh(x)\oplus1\) 表示异或 \(1\),用来取另一个的儿子的方向。
对于 \(z\):\(ch[z][wh(y)]=x\)
对于 \(y\):\(fa[y]=x,ch[y][wh(x)]=ch[x][wh(x)\oplus1]\)
对于 \(x\):\(fa[x]=z,ch[x][wh(x)\oplus1]=y\)
对于 \(ch[x][wh(x)\oplus1]\):\(fa[ch[x][wh(x)\oplus1]]=y\)
把上述变化写成代码即可实现旋转。注意上述变化是同时发生的,旋转时需要注意不能互相影响。定义根节点父亲为 \(0\),此时不需要特判 \(z\) 不存在,因为代入发现没有影响。
void rotate(int x)
{
int y=f[x],z=f[y],k=wh(x);
ch[z][wh(y)]=x;
f[x]=z;
ch[y][k]=ch[x][k^1];
f[ch[x][k^1]]=y;
ch[x][k^1]=y;
f[y]=x;
pushup(y);pushup(x);
}
接下来,我们可以开始讲 Treap 的核心思想了。Treap 在保证需要维护的数值满足二叉搜索树性质外,对于每一个节点额外记录一个随机赋予权值,并通过旋转使这个权值符合大根堆性质。可以证明树高都期望为 \(\log n\) 级别,因为这样做相当于随机生成一棵树,随机生成的树期望深度为 \(\log n\),故每次操作的期望时间复杂度为 \(O(\log n)\)。
创建新节点
最简单的一部分,随机赋予权值用于保持树的平衡,其余的信息正常维护。\(tol[x]\) 表示节点 \(x\) 的元素数量,因为可能会有重复元素。
int create(int v)
{
val[++cnt]=v;
key[cnt]=rand();
siz[cnt]=1;
tol[cnt]=1;
return cnt;
}
信息上传
类似于 【6】线段树学习笔记 中线段树的信息上传,把子节点的信息合并到父节点上。注意特判子节点不存在的情况。下面是一个维护子树大小的例子,此时不需要特判。
void pushup(int now)
{
siz[now]=siz[ch[now][0]]+siz[ch[now][1]]+tol[now];
}
建树
为了便于应对查询时出界的情况,我们设立两个哨兵节点,一个为正无穷,一个为负无穷。显然,正无穷节点是负无穷的右子树。顺便初始化根的编号。
void build()
{
root=create(-inf),ch[root][1]=create(inf);
pushup(root);
}
插入
考虑从根开始遍历,通过比较与当前节点维护的信息的大小决定是往左儿子走或右儿子走。如果走到空节点,则新建一个节点维护这个插入到值。之后,在回溯的过程中判断节点的权值与其发生变化的儿子节点权值的关系,如果儿子节点权值更大,则旋转以保证大根堆性质。特别的,如果走到与当前节点维护的信息的大小相同的节点,证明有重复,直接累加即可。
void insert(int &now,int v)
{
if(now==0)
{
now=create(v);
return;
}
if(v==val[now])tol[now]++;
else
{
int to=0;
if(v<val[now])to=0;
else to=1;
insert(ch[now][to],v);
if(key[now]<key[ch[now][to]])rotate(now,to^1);
}
pushup(now);
}
删除
与插入基本一样,同样的递归方法,如果走到与当前节点维护的信息的大小相同的节点,直接将这个节点的计数减 \(1\)。如果减 \(1\) 后计数为 \(0\),证明节点被删空,我们的策略是被这个节点旋转到叶子,避免之后对树产生影响。特别的,若走到空节点,证明被删除的元素不存在,直接返回。
在转到叶子节点的过程中,为了满足大根堆性质,我们选择权值较小的子节点交换。
void del(int &now,int v)
{
if(now==0)return;
if(v==val[now])
{
if(tol[now]>1)
{
tol[now]--;
pushup(now);
return;
}
else if(ch[now][0]||ch[now][1])
{
if(!ch[now][1]||key[ch[now][0]]>key[ch[now][1]])rotate(now,1),del(ch[now][1],v);
else rotate(now,0),del(ch[now][0],v);
pushup(now);
}
else now=0;
return;
}
else
{
int to=0;
if(v<val[now])to=0;
else to=1;
del(ch[now][to],v);
pushup(now);
}
}
由排名查数值
类似于 【6】线段树学习笔记 中权值线段树的查排名,查询排名为 \(k\) 的数相当于查询第 \(k\) 小的数。考虑维护子树大小 \(siz[x]\) 与当前节点的值的出现次数 \(cnt[x]\)。
\(1\):\(k\le siz[ch[x][0]]\),表示维护的值小于当前值的数的数量大于等于 \(k\),那么第 \(k\) 小必然在小于当前值的数中,递归访问左儿子,查询第 \(k\) 小。特别的,如果 \(ch[x][0]+cnt[x]\ge k\),直接返回当前维护的值,因为需要查询的数就在这个节点。
\(2\):\(k\gt siz[ch[x][0]]\),表示维护的值大于当前值的数的数量小于 \(k\),那么第 \(k\) 小必然在大于当前值的数中,递归访问右儿子,查询第 \(k-v[ch[x][0]]-cnt[x]\) 小,因为有 \(v[ch[x][0]]\) 个数在左儿子中,\(cnt[x]\) 个数在当前节点。
int query(int now,int rk)
{
int sum=0;
if(now==0)return 99999999;
else if(rk<=siz[ch[now][0]])return query(ch[now][0],rk);
else if(rk<=siz[ch[now][0]]+tol[now])return val[now];
else return query(ch[now][1],rk-siz[ch[now][0]]-tol[now]);
}
由数值查排名
由于平衡树满足二叉搜索树性质,所有我们可以根据某个数与当前节点的大小关系决定下一步走的方向。设我们查询的数为 \(k\),当前节点为 \(x\)。
\(1\):\(a[x]=k\),我们已经找到了数 \(x\) 代表的节点,这个节点的左子树中的节点都小于 \(x\),直接返回排名。注意排名除了小于 \(k\) 的数的数量还需要加 \(1\),所以返回 \(siz[ch[x][0]]+1\)。
\(2\):\(a[x]\gt k\),节点 \(x\) 左子树中可能存在大于 \(k\) 的数,我们暂时无法确定。但是节点 \(x\) 右子树中的点权值大于 \(a[x]\),也大于 \(k\),又因为排名为 \(y\) 的数相当于有 \(y-1\) 个数比它小,只需要考虑比 \(k\) 小的数,所以对 \(k\) 的排名没有影响,不需要考虑右子树,直接递归左子树即可。
\(3\):\(a[x]\lt k\),节点 \(x\) 左子树以及节点 \(x\) 都小于 \(k\),因为排名为 \(y\) 的数相当于有 \(y-1\) 个数比它小,我们直接把这些数的数量加在排名上,即 \(siz[ch[x][0]]+tol[x]\)。之后,由于节点 \(x\) 右子树可能存在小于 \(k\) 的元素,我们递归右子树。通过回溯累加排名。
特别的,如果我们走到了一个空节点,为了保证是小于 \(k\) 的数的数量加 \(1\),我们返回 \(1\)。
int ranking(int now,int v)
{
if(now==0)return 1;
if(v==val[now])return siz[ch[now][0]]+1;
else if(v<val[now])return ranking(ch[now][0],v);
else return siz[ch[now][0]]+tol[now]+ranking(ch[now][1],v);
}
前驱与后继
对于求 \(x\) 的前驱,我们从根开始,一直往下搜索。如果这个节点的权值小于 \(x\),则可以成为 \(x\) 的前驱,令答案为这个节点的权值,之后访问它的右儿子,因为可能存在比这个节点值更大但是小于 \(x\) 的值。否则就递归去找比这个节点权值小的值,访问左儿子,因为比这个权值大的值不可能成为前驱。
int pre(int x)
{
int now=root,ans=0;
while(now)
{
if(x<=val[now])now=ch[now][0];
else ans=val[now],now=ch[now][1];
}
return ans;
}
对于后继其实也是同理,我们从根开始,一直往下搜索。如果这个节点的权值大于 \(x\),则可以成为 \(x\) 的后继,令答案为这个节点的权值,之后访问它的左儿子,因为可能存在比这个节点值更小但是大于 \(x\) 的值。否则就递归去找比这个节点权值大的值,访问右儿子,因为比这个权值小的值不可能成为后继。
int nxt(int x)
{
int now=root,ans=0;
while(now)
{
if(x>=val[now])now=ch[now][1];
else ans=val[now],now=ch[now][0];
}
return ans;
}
Splay
Splay 和 Treap 的大部分操作是完全一样的,也符合 Treap 的性质。它们之间唯一的区别在于维护树的平衡的方式。
Splay
Splay 的主要思想是在旋转一个节点时,考虑这个节点和其父亲与祖父之间的关系。如果这个节点和这个节点的父节点都是其父亲的左/右儿子节点,那我们就先旋转父亲,再旋转儿子。否则我们先旋转儿子,再旋转父亲。
Splay 具有一个独特的 splay(x,to) 操作,作用是把点 \(x\) 旋转到根或某一个节点 \(to\) 底下。每次旋转如果需要旋转父亲,就使用上面的旋转方式。否则只旋转自己。一般我们操作一个节点会将其旋转到根,所以一般默认 \(to\) 为 \(0\),有时会省略不写。(写法 \(1\))
实现时需要注意如果旋转到根节点需要更新根节点。代码中的 wh(x) 定义同 Treap 中的 wh(x)。
void splay(int x,int to)
{
while(f[x]!=to)
{
int y=f[x],z=f[y];
if(z!=to)
{
if(wh(x)==wh(y))rotate(y);
else rotate(x);
}
rotate(x);
}
if(to==0)root=x;
}
如果有多棵 Splay 可能需要传入更新哪个根作为参数,使用引用可以轻松解决这个问题。这里是默认旋转到根,并顺便更新根。(写法 \(2\))
void splay(int &rt,int x)
{
while(fa[x])
{
int y=fa[x];
if(fa[y])
{
if(wh(x)==wh(y))rotate(y);
else rotate(x);
}
rotate(x);
}
rt=x;
}
我们感性理解 Splay 的时间复杂度,每次旋转会导致一条链的长度减半,所以时间复杂度均摊 \(O(\log n)\)。理性分析需要使用势能分析法,可以参考 这个视频。大致就是定义一个节点的势能 \(\phi(x)\) 为 \(\log_{2} \text{siz}[x]\),其中 \(\text{siz}[x]\) 表示节点 \(x\) 的子树大小,然后考虑旋转时的势能和变化,通过合理放缩得到时间复杂度。
一般我们会在每次操作一个点之后将其 splay 到根,这样做有两个好处:一是多次旋转使树尽可能平衡,注意到查询时也要 splay,不然复杂度就爆了;二是顺便通过 rotate 中的 pushup 上传信息。
插入
插入和 Treap 基本一样,只不过最后的旋转调整改为了直接 splay 到根。有两种写法,递归版和非递归版。这里展示递归版,非递归版可以看例题 \(5\)。(这里的 splay 是写法 \(1\))
void insert(int &now,int v,int fa)
{
if(now==0)
{
now=create(v,fa);
return;
}
if(v==val[now])return;
else
{
int to=0;
if(v<val[now])to=0;
else to=1;
insert(ch[now][to],v,now);
}
pushup(now);
splay(now,0);
}
注意插入完成之后需要 splay。
删除&无交合并
找到删除的数对应的节点,直接旋转到根删除。现在有两棵子树,我们在被删除的节点的右子树找到最小值 splay 到右子树的根,此时一定没有左儿子。根据 Treap 的性质,被删除的节点的左子树所有节点一定小于被删除的节点的右子树的最小值,所以直接把被删除的节点的左子树接在被删除的节点的右子树的根的左儿子即可。(这里的 splay 是写法 \(2\))
下面是非递归写法。
void erase(int rt,int k)
{
int x=rt;
while(x)
{
if(k==val[x])
{
num[x]--,splay(rt,x);
if(num[x]==0)
{
fa[ch[x][0]]=fa[ch[x][1]]=0;
int p=getmin(ch[x][1]);
splay(ch[x][1],p),ch[ch[x][1]][0]=ch[x][0],fa[ch[x][0]]=ch[x][1],rt=ch[x][1],pushup(ch[x][1]);
}
return;
}
else if(k<val[x])x=ch[x][0];
else x=ch[x][1];
}
}
这其实也是平衡树无交合并的方法。
求最小值上文没提到,但是很简单,一直往左儿子走直到没有左儿子就是最小值。求最大值改为一直往右儿子就行了。记得 splay。
int getmin(int rt)
{
int x=rt;
while(ch[x][0])x=ch[x][0];
splay(x);
return x;
}
按值分裂
先在平衡树中找到最小的大于给定值 \(k\) 的元素,可以在平衡树上走路更新答案得到,小于等于 \(k\) 直接走右子树,大于 \(k\) 就更新答案后走左子树。之后把 \(k\) 旋转到根,断开左子树的连接,就把平衡树分裂成了两棵树。
代码中 \(rt\) 为根的树中存储大于 \(k\) 的数,返回的 \(nrt\) 为根的树中存储小于等于 \(k\) 的数。注意为空时的特判和 splay 路径上的节点。
long long split(long long &rt,long long k)
{
long long x=rt,ap=0,pr=0,ans=1e18;
while(x)
{
pr=x,pushdown(x);
if(k>=val[x])x=ch[x][1];
else if(k<val[x])
{
if(val[x]<=ans)ans=val[x],ap=x;
x=ch[x][0];
}
}
splay(rt,pr);
if(ap==0)
{
int nrt=rt;
rt=0;
return nrt;
}
splay(rt,ap);
int nrt=ch[rt][0];
fa[ch[rt][0]]=0,ch[rt][0]=0;
return nrt;
}
有交合并
合并两棵平衡树,考虑先找出一棵树的最小值 \(mi\),在另一棵子树中把小于等于 \(mi\) 的元素分裂出来,和这棵树无交合并,再对另一棵树执行这个操作。交替执行,直到一棵树为空,可以证明 至多操作 \(O(\log n)\) 次,同样使用势能分析,总时间复杂度 \(O(\log^2n)\)。
int merge(int &rt1,int &rt2)
{
bool flag=0;
while(rt1&&rt2)
{
if(!flag)
{
int p=getmin(rt1),nrt=0;
splay(rt1,p),nrt=split(rt2,val[p]),fa[nrt]=p,ch[p][0]=nrt;
}
else
{
int p=getmin(rt2),nrt=0;
splay(rt2,p),nrt=split(rt1,val[p]),fa[nrt]=p,ch[p][0]=nrt;
}
flag^=1;
}
return rt1+rt2;
}
其余操作
和 Treap 完全一样,不多赘述。
FHQ-Treap
FHQ-Treap 是一种不基于旋转操作的平衡树,它的核心原理是通过不断分裂与合并的过程完成对树的平衡。和 Treap 一样,FHQ-Treap 也需要随机赋权,并使权值满足大根堆的性质。因此,FHQ-Treap 的时间复杂度分析与 Treap 一样,相当于随机树的深度,即 \(O(\log n)\)。
在常数上一般比 Splay 有优势,但它们都比 Treap 慢。所以我们把除 Splay 和 FHQ-Treap 以外的 \(O(\log n)\) 的平衡树叫做高速平衡树。
分裂
FHQ-Treap 通常的分裂方式为按值分裂,即传入参数 \(k\),把整个树按节点存储数据的权值分裂成 \(\le k\) 和 \(\gt k\) 的两棵树。
我们通过函数 split(int p,int k,int &x,int &y) 来完成该操作。其中,\(p\) 为当前节点,\(x,y\) 为引用,分别表示在 \(\le k\) 和 \(\gt k\) 的两棵树中如果加入当前节点那当前节点应该处于的位置(即是哪一个节点的左或右儿子)。
我们先比较当前节点 \(p\) 权值 \(v\) 和 \(k\) 的大小,如果 \(v\le k\),则说明当前节点以及其左子树节点都 \(\le k\),直接划至 \(\le k\) 的树中对应的位置,因为有引用,所以我们可以直接 \(x=p\)。然后我们需要继续分裂右子树,此时右子树节点分裂出来 \(\le k\) 的部分显然应该被划分到 \(p\) 的右子树,而 \(\gt k\) 的部分由于节点 \(p\) 对 \(\gt k\) 的树没有影响所以继承原位置,那我们递归调用 split(ch[p][1],k,ch[p][1],y) 即可。
\(v\gt k\) 也是同理,注意边界空节点时返回。
void split(int p,int k,int &x,int &y)
{
if(!p)x=y=0;
else
{
if(tr[p].val<=k)
{
x=p;
split(ch[p][1],k,ch[p][1],y);
}
else
{
y=p;
split(ch[p][0],k,ch[p][0],y);
}
pushup(p);
}
}
合并
FHQ-Treap 的合并仅支持无交合并,并不能解决有交合并的问题。对于有交合并还是需要采用 Splay 中提到的化有交合并为无交合并的方式。
我们利用函数 merge(int x,int y) 实现这一过程,其中 \(x,y\) 分别为存储的数据值较小的一棵树和数据值较大的一棵树的根,函数的返回值为合并后的根节点。
由于是无交合并,所以节点之间合并方式比较确定,要么把 \(y\) 合并到 \(x\) 的右子树,然后就是 \(y\) 和 \(x\) 的右子树合并,即递归 merge(ch[x][1],y),并更新 \(x\) 的右儿子,即 \(ch[x][1]=merge(ch[x][1],y)\),要么把 \(x\) 合并到 \(y\) 的左子树。为了维护大根堆的性质,我们把 \(x,y\) 中随机权值较大的那一个放在根,把另一个合并为子树。
注意这里比较的是随机权值而不是存储数据的权值,然后注意一下边界,\(x,y\) 中某一个为空时返回另一个。
int merge(int x,int y)
{
if(!x||!y)return x+y;
if(tr[x].key>tr[y].key)
{
ch[x][1]=merge(ch[x][1],y);
pushup(x);
return x;
}
else
{
ch[y][0]=merge(x,ch[y][0]);
pushup(y);
return y;
}
}
插入
FHQ-Treap 的插入就非常爽了,假设插入的元素值为 \(k\),先建立一个值为 \(k\) 的 \(y\) 节点,把原树按 \(k\) 分裂为 \(\le k\) 的部分子树 \(x\) 和 \(\gt k\) 的部分子树 \(z\),然后由于不交,所以顺次合并 \(x,y,z\) 即可。
void insert(int k)
{
int x=0,y=create(k),z=0;
split(rt,k,x,z);
rt=merge(merge(x,y),z);
}
删除
FHQ-Treap 的删除就更爽了,假设删除的元素值为 \(k\),先分裂出 \(\le k\) 的子树 \(x\),再在 \(x\) 中分裂出 \(\gt k-1\) 的子树 \(y\),这样 \(y\) 的根节点就是我们需要删除的元素,然后把 \(y\) 的根节点的左儿子和右儿子一合并,\(y\) 的根节点就自动被删除了,最后把分裂出的一堆子树合并就完成了。
void del(int k)
{
int x=0,y=0,z=0;
split(rt,k,x,z);
split(x,k-1,x,y);
y=merge(ch[y][0],ch[y][1]);
rt=merge(merge(x,y),z);
}
其余操作
和 Splay 完全一样,不多赘述。
例题
例题 \(1\) :
本题是平衡树维护集合的经典运用。
普通平衡树模板题,不多赘述。这里没有维护父亲节点,所以旋转写的比较不一样,是另一种码风。
#include <bits/stdc++.h>
using namespace std;
int n,op,x,ch[1000040][2],val[1000040],key[1000040],siz[1000040],tol[1000040],cnt=0,root=0;
int create(int v)
{
val[++cnt]=v;
key[cnt]=rand();
siz[cnt]=1;
tol[cnt]=1;
return cnt;
}
void pushup(int now)
{
siz[now]=siz[ch[now][0]]+siz[ch[now][1]]+tol[now];
}
void build()
{
root=create(-99999999),ch[root][1]=create(99999999);
pushup(root);
}
void rotate(int &now,int to)
{
int tmp=ch[now][to^1];
ch[now][to^1]=ch[tmp][to];
ch[tmp][to]=now;
now=tmp;
pushup(ch[now][to]);pushup(now);
}
void insert(int &now,int v)
{
if(now==0)
{
now=create(v);
return;
}
if(v==val[now])tol[now]++;
else
{
int to=0;
if(v<val[now])to=0;
else to=1;
insert(ch[now][to],v);
if(key[now]<key[ch[now][to]])rotate(now,to^1);
}
pushup(now);
}
void del(int &now,int v)
{
if(now==0)return ;
if(v==val[now])
{
if(tol[now]>1)
{
tol[now]--;
pushup(now);
return ;
}
else if(ch[now][0]||ch[now][1])
{
if(!ch[now][1]||key[ch[now][0]]>key[ch[now][1]])rotate(now,1),del(ch[now][1],v);
else rotate(now,0),del(ch[now][0],v);
pushup(now);
}
else now=0;
return ;
}
else
{
int to=0;
if(v<val[now])to=0;
else to=1;
del(ch[now][to],v);
pushup(now);
}
}
int ranking(int now,int v)
{
if(now==0)return 1;
if(v==val[now])return siz[ch[now][0]]+1;
else if(v<val[now])return ranking(ch[now][0],v);
else return siz[ch[now][0]]+tol[now]+ranking(ch[now][1],v);
}
int query(int now,int rk)
{
int sum=0;
if(now==0)return 99999999;
else if(rk<=siz[ch[now][0]])return query(ch[now][0],rk);
else if(rk<=siz[ch[now][0]]+tol[now])return val[now];
else return query(ch[now][1],rk-siz[ch[now][0]]-tol[now]);
}
int pre(int x)
{
int now=root,ans=0;
while(now)
{
if(x<=val[now])now=ch[now][0];
else ans=val[now],now=ch[now][1];
}
return ans;
}
int nxt(int x)
{
int now=root,ans=0;
while(now)
{
if(x>=val[now])now=ch[now][1];
else ans=val[now],now=ch[now][0];
}
return ans;
}
int main()
{
scanf("%d",&n);
build();
for(int i=1;i<=n;i++)
{
scanf("%d%d",&op,&x);
if(op==1)insert(root,x);
else if(op==2)del(root,x);
else if(op==3)printf("%d\n",ranking(root,x)-1);
else if(op==4)printf("%d\n",query(root,x+1));
else if(op==5)printf("%d\n",pre(x));
else if(op==6)printf("%d\n",nxt(x));
}
return 0;
}
例题 \(2\) :
本题是平衡树维护集合的经典运用。
我们考虑维护两棵平衡树,一棵维护宠物的特点值,另一棵维护顾客的特点值。插入宠物判断是否有多余的顾客,如果有就查询前驱和后继,选择距离较近的,如果一样近就选前驱,之后删除匹配上的节点。否则直接插进宠物树。插入顾客也是同理。
#include <bits/stdc++.h>
using namespace std;
long long n,op,x,ch[100000][2],val[100000],key[100000],siz[100000],tol[100000],cnt=0,rt1=0,rt2=0,sum=0;
const long long mod=1000000;
long long create(long long v)
{
val[++cnt]=v;
key[cnt]=rand();
siz[cnt]=1;
tol[cnt]=1;
return cnt;
}
void pushup(long long now)
{
siz[now]=siz[ch[now][0]]+siz[ch[now][1]]+tol[now];
}
void build()
{
rt1=create(-1e18),ch[rt1][1]=create(1e18);
rt2=create(-1e18),ch[rt2][1]=create(1e18);
pushup(rt1),pushup(rt2);
}
void rotate(long long &now,long long to)
{
long long tmp=ch[now][to^1];
ch[now][to^1]=ch[tmp][to];
ch[tmp][to]=now;
now=tmp;
pushup(ch[now][to]);pushup(now);
}
void insert(long long &now,long long v)
{
if(now==0)
{
now=create(v);
return;
}
if(v==val[now])tol[now]++;
else
{
long long to=0;
if(v<val[now])to=0;
else to=1;
insert(ch[now][to],v);
if(key[now]<key[ch[now][to]])rotate(now,to^1);
}
pushup(now);
}
void del(long long &now,long long v)
{
if(now==0)return ;
if(v==val[now])
{
if(tol[now]>1)
{
tol[now]--;
pushup(now);
return ;
}
else if(ch[now][0]||ch[now][1])
{
if(!ch[now][1]||key[ch[now][0]]>key[ch[now][1]])rotate(now,1),del(ch[now][1],v);
else rotate(now,0),del(ch[now][0],v);
pushup(now);
}
else now=0;
return ;
}
else
{
long long to=0;
if(v<val[now])to=0;
else to=1;
del(ch[now][to],v);
pushup(now);
}
}
long long pre(long long x,long long rt)
{
long long now=rt,ans=0;
while(now)
{
if(x<=val[now])now=ch[now][0];
else ans=val[now],now=ch[now][1];
}
return ans;
}
long long nxt(long long x,long long rt)
{
long long now=rt,ans=0;
while(now)
{
if(x>=val[now])now=ch[now][1];
else ans=val[now],now=ch[now][0];
}
return ans;
}
int main()
{
scanf("%lld",&n);
build();
for(int i=1;i<=n;i++)
{
scanf("%lld%lld",&op,&x);
if(op==0)
{
long long x1=pre(x,rt2),x2=nxt(x,rt2),ans=0;
if(x-x1<=x2-x)ans=x1;
else ans=x2;
if(abs(ans)==1e18)insert(rt1,x);
else del(rt2,ans),sum+=abs(x-ans),sum%=mod;
}
else if(op==1)
{
long long x1=pre(x,rt1),x2=nxt(x,rt1),ans=0;
if(x-x1<=x2-x)ans=x1;
else ans=x2;
if(abs(ans)==1e18)insert(rt2,x);
else del(rt1,ans),sum+=abs(x-ans),sum%=mod;
}
}
printf("%lld\n",sum);
return 0;
}
例题 \(3\) :
本题是平衡树维护序列的经典运用。
我们用平衡树的一个节点表示区序列一个位置,维护这个位置的有关信息,并将这个位置作为平衡树上二叉搜索树性质的权值。此时,我们中序遍历这棵平衡树,就能输出整个序列。
我们考虑提取一段区间,我们先在平衡树找到左端点 \(l-1\) 对应的节点,将其旋转到根,再找到右端点 \(r+1\) 对应的节点,将其旋转到 \(l-1\) 底下。这样,平衡树根节点右儿子的左儿子对应的子树就是 \((l-1,r+1)\) 的区间,即 \([l,r]\),对区间操作,就是对这棵子树操作。
注意这里的权值 \(x\) 表示在序列中实际上是第几个位置,因为是中序遍历,所以可以通过 \(siz\) 子树大小反应出这是第几个位置。即先找出前 \(l-1\) 个数对应的位置,再找出前 \(r+1\) 个数对应的位置,相当于由排名查数值。
这个操作比较重要就单独列出来。query(rt,x) 表示在以 rt 为根的子树中查询二叉搜索树性质的权值为 \(x\) 的点,splay(x,y) 表示把 \(x\) 转到 \(y\) 下面,\(y=0\) 即转为根。update(x) 表示对子树 \(x\) 进行操作。区间查询也是类似。
void modify(int l,int r)
{
l=query(root,l-1),r=query(root,r+1);
splay(l,0),splay(r,l);
update(ch[ch[root][1]][0]]);
}
现在我们考虑如何维护区间翻转。我们发现,区间翻转其实就是交换节点 \(x\) 的左右子树,之后再到左右子树中进行同样的操作。我们写一个懒标记实现交换,每次走到一个节点时下传懒标记。我们一般还会在 splay 的时候把其祖先的懒标记全部下传,写一个栈每次求出所有祖先从高到低下传标记,这里由于写法不需要。
代码中为了避免越界插入了正无穷和负无穷,所以修改时要改为 l=query(root,l),r=query(root,r+2),注意一下。
#include <bits/stdc++.h>
using namespace std;
int n,m,l,r,ch[1000040][2],val[1000040],siz[1000040],f[1000040],mk[1000040],cnt=0,root=0;
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int create(int v,int fa)
{
val[++cnt]=v;
siz[cnt]=1;
f[cnt]=fa;
return cnt;
}
bool wh(int x)
{
return ch[f[x]][1]==x;
}
void pushup(int now)
{
siz[now]=siz[ch[now][0]]+siz[ch[now][1]]+1;
}
void pushdown(int now)
{
if(mk[now])
{
swap(ch[now][0],ch[now][1]);
mk[ch[now][0]]^=1,mk[ch[now][1]]^=1,mk[now]=0;
}
}
void rotate(int x)
{
int y=f[x],z=f[y],k=wh(x);
ch[z][wh(y)]=x;
f[x]=z;
ch[y][k]=ch[x][k^1];
f[ch[x][k^1]]=y;
ch[x][k^1]=y;
f[y]=x;
pushup(y);pushup(x);
}
void splay(int x,int to)
{
while(f[x]!=to)
{
int y=f[x],z=f[y];
if(z!=to)
{
if(wh(x)==wh(y))rotate(y);
else rotate(x);
}
rotate(x);
}
if(to==0)root=x;
}
void insert(int &now,int v,int fa)
{
if(now==0)
{
now=create(v,fa);
return;
}
if(v==val[now])return;
else
{
int to=0;
if(v<val[now])to=0;
else to=1;
insert(ch[now][to],v,now);
}
pushup(now);
splay(now,0);
}
void build()
{
root=create(-99999999,0),ch[root][1]=create(99999999,root);
pushup(root);
for(int i=1;i<=n;i++)insert(root,i,0);
}
int query(int now,int rk)
{
pushdown(now);
if(now==0)return 99999999;
if(rk<=siz[ch[now][0]])return query(ch[now][0],rk);
if(rk<=siz[ch[now][0]]+1)return now;
return query(ch[now][1],rk-siz[ch[now][0]]-1);
}
void reverse(int l,int r)
{
l=query(root,l),r=query(root,r+2);
splay(l,0),splay(r,l);
mk[ch[ch[root][1]][0]]^=1;
}
void print(int x)
{
pushdown(x);
if(ch[x][0])print(ch[x][0]);
if(val[x]>=1&&val[x]<=n)printf("%d ",val[x]);
if(ch[x][1])print(ch[x][1]);
}
int main()
{
n=read(),m=read();
build();
while(m--)
{
l=read(),r=read();
reverse(l,r);
}
print(root);
return 0;
}
本题还有 FHQ-Treap 的解法,按排名分裂,套用由排名查数值的方式,先分裂出前 \(l-1\) 个数构成一棵子树,再到另一棵子树中分类出前 \(r-l+1\) 个数构成的子树打上标记,最后合并回去。
#include<bits/stdc++.h>
using namespace std;
struct fhq
{
int val,key,siz,tg;
}tr[200000];
int n,m,ch[200000][2],l,r,cnt=0,rt=0;
mt19937 rd(time(NULL));
void pushup(int x)
{
tr[x].siz=tr[ch[x][0]].siz+tr[ch[x][1]].siz+1;
}
void pushdown(int x)
{
if(tr[x].tg)
{
tr[ch[x][0]].tg^=1,tr[ch[x][1]].tg^=1,tr[x].tg=0;
swap(ch[ch[x][0]][0],ch[ch[x][0]][1]);
swap(ch[ch[x][1]][0],ch[ch[x][1]][1]);
}
}
int create(int k)
{
tr[++cnt].val=k,tr[cnt].key=rd(),tr[cnt].tg=0,tr[cnt].siz=1;
return cnt;
}
void split(int p,int k,int &x,int &y)
{
if(!p)x=y=0;
else
{
pushdown(p);
if(tr[ch[p][0]].siz+1<=k)
{
x=p;
split(ch[p][1],k-tr[ch[p][0]].siz-1,ch[p][1],y);
}
else
{
y=p;
split(ch[p][0],k,x,ch[p][0]);
}
pushup(p);
}
}
int merge(int x,int y)
{
if(!x||!y)return x+y;
pushdown(x),pushdown(y);
if(tr[x].key>tr[y].key)
{
ch[x][1]=merge(ch[x][1],y);
pushup(x);
return x;
}
else
{
ch[y][0]=merge(x,ch[y][0]);
pushup(y);
return y;
}
}
void insert(int k)
{
int x=0,y=create(k),z=0;
split(rt,k,x,z);
rt=merge(merge(x,y),z);
}
void reverse(int l,int r)
{
int x=0,y=0,z=0,w=0;
split(rt,l-1,x,y);
split(y,r-l+1,z,w);
tr[z].tg^=1,swap(ch[z][0],ch[z][1]);
rt=merge(x,merge(z,w));
}
void print(int x)
{
pushdown(x);
if(ch[x][0])print(ch[x][0]);
printf("%d ",tr[x].val);
if(ch[x][1])print(ch[x][1]);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)insert(i);
for(int i=1;i<=m;i++)scanf("%d%d",&l,&r),reverse(l,r);
print(rt);
return 0;
}
例题 \(4\) :
本题是平衡树上维护懒标记的经典运用。
本题和上一个题基本一样,只不过多了一个求最大值和加法。最大值是容易的,上传信息的时候直接使用 pushup 维护子树内即可。加法也是容易的,考虑设置一个加法懒标记,下传时更新最大值。加法标记和翻转标记不会互相影响。
#include <bits/stdc++.h>
using namespace std;
long long n,m,op,l,r,k,ch[100000][2],val[100000],a[100000],siz[100000],f[100000],re[100000],mx[100000],ad[100000],st[100000],top=0,cnt=0,rt=0;
inline long long read()
{
long long x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
long long create(long long v,long long fa)
{
val[++cnt]=v;
siz[cnt]=1;
f[cnt]=fa;
mx[cnt]=0;
return cnt;
}
bool wh(long long x)
{
return ch[f[x]][1]==x;
}
void pushup(long long now)
{
siz[now]=siz[ch[now][0]]+siz[ch[now][1]]+1;
mx[now]=a[now];
if(ch[now][0])mx[now]=max(mx[now],mx[ch[now][0]]);
if(ch[now][1])mx[now]=max(mx[now],mx[ch[now][1]]);
}
void pushdown(long long now)
{
if(ch[now][0])a[ch[now][0]]+=ad[now],mx[ch[now][0]]+=ad[now],ad[ch[now][0]]+=ad[now];
if(ch[now][1])a[ch[now][1]]+=ad[now],mx[ch[now][1]]+=ad[now],ad[ch[now][1]]+=ad[now];
ad[now]=0;
if(re[now])
{
swap(ch[now][0],ch[now][1]);
if(ch[now][0])re[ch[now][0]]^=1;
if(ch[now][1])re[ch[now][1]]^=1;
re[now]=0;
}
}
void rotate(long long x)
{
long long y=f[x],z=f[y],k=wh(x);
if(z)ch[z][wh(y)]=x;
f[x]=z,f[y]=x,f[ch[x][k^1]]=y;
ch[y][k]=ch[x][k^1],ch[x][k^1]=y;
pushup(y),pushup(x);
}
void splay(long long x,long long to)
{
top=0,st[++top]=x;
for(int i=x;f[i];i=f[i])st[++top]=f[i];
while(top)pushdown(st[top]),top--;
while(f[x]!=to)
{
long long y=f[x],z=f[y];
if(z!=to)
{
if(wh(x)==wh(y))rotate(y);
else rotate(x);
}
rotate(x);
}
if(to==0)rt=x;
}
void insert(long long &now,long long v,long long fa)
{
if(now==0)
{
now=create(v,fa);
return;
}
if(v==val[now])return;
else insert(ch[now][v>val[now]],v,now);
pushup(now),splay(now,0);
}
void build()
{
rt=create(-1e18,0),ch[rt][1]=create(1e18,rt);
pushup(rt);
for(long long i=1;i<=n;i++)insert(rt,i,0);
}
long long query(long long now,long long rk)
{
pushdown(now);
if(now==0)return 1e18;
if(rk<=siz[ch[now][0]])return query(ch[now][0],rk);
if(rk<=siz[ch[now][0]]+1)return now;
return query(ch[now][1],rk-siz[ch[now][0]]-1);
}
void reverse(long long l,long long r)
{
pushdown(rt);
l=query(rt,l),r=query(rt,r+2);
splay(l,0),splay(r,l);
re[ch[ch[rt][1]][0]]^=1;
}
void add(long long l,long long r,long long k)
{
pushdown(rt);
l=query(rt,l),r=query(rt,r+2);
splay(l,0),splay(r,l);
a[ch[ch[rt][1]][0]]+=k,mx[ch[ch[rt][1]][0]]+=k,ad[ch[ch[rt][1]][0]]+=k;
}
long long getmax(long long l,long long r)
{
pushdown(rt);
l=query(rt,l),r=query(rt,r+2);
splay(l,0),splay(r,l);
return mx[ch[ch[rt][1]][0]];
}
int main()
{
n=read(),m=read();
build();
while(m--)
{
op=read();
if(op==1)l=read(),r=read(),k=read(),add(l,r,k);
else if(op==2)l=read(),r=read(),reverse(l,r);
else if(op==3)l=read(),r=read(),printf("%lld\n",getmax(l,r));
}
return 0;
}
例题 \(5\) :
P11622 [Ynoi Easy Round 2025] TEST_176
本题是插入-标记-回收算法和平衡树有交合并的经典运用。
把询问离线下来,从左到右扫描整个序列,如果遇到了某个询问的左端点就把这个询问中的数插入数据结构,之后更新添加这一位置的元素对数据结构中的元素的影响,在询问的右端点影响处理完成之后再回收这个元素查询,可以直接删除。这是 lxl 在知码狐北京集训时讲的插入-标记-回收算法。
回到这个题,我们只需要选择一个数据结构,并处理每个位置的数的贡献即可。线段树很难处理对单个元素的影响,考虑平衡树。插入和查询比较容易,插入时记录位置查询时直接查即可。
每次更新新的位置时,考虑什么样的数会被影响,有 \(a_i-x\gt x\),即 \(x\lt\frac{a_i}{2}\)。由于 \(a_i\) 是整数,所以等价于 \(x\le\lfloor\frac{a_i-1}{2}\rfloor\)。于是我们把平衡树按照 \(\lfloor\frac{a_i-1}{2}\rfloor\) 分裂,在 \(\le\lfloor\frac{a_i-1}{2}\rfloor\) 的那棵子树上先进行整体取反,然后再整体加 \(a_i\),之后再有交合并这两棵树。
整体取反和整体加都可以通过打标记实现,注意先下传整体取反标记再下传整体加标记。轻微卡常。
#include<bits/stdc++.h>
using namespace std;
int n,m,li,ri,ch[200002][2],fa[200002],rev[200002],st[200002],y[200002],top=0,cnt=1,rt=1;
long long ci,a[200002],val[200002],ad[200002],ans[200002];
vector<int>l[200002],r[200002];
vector<long long>c[200002];
inline long long read()
{
long long x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
void print(long long x)
{
if(x<0)putchar('-'),x=-x;
if(x>9)print(x/10);
putchar('0'+x%10);
}
bool wh(int x)
{
return ch[fa[x]][1]==x;
}
void pushdown(int x)
{
if(rev[x])
{
if(ch[x][0])rev[ch[x][0]]^=1,val[ch[x][0]]*=-1,ad[ch[x][0]]*=-1,swap(ch[ch[x][0]][0],ch[ch[x][0]][1]);
if(ch[x][1])rev[ch[x][1]]^=1,val[ch[x][1]]*=-1,ad[ch[x][1]]*=-1,swap(ch[ch[x][1]][0],ch[ch[x][1]][1]);
rev[x]=0;
}
if(ch[x][0])val[ch[x][0]]+=ad[x],ad[ch[x][0]]+=ad[x];
if(ch[x][1])val[ch[x][1]]+=ad[x],ad[ch[x][1]]+=ad[x];
ad[x]=0;
}
void rotate(int x)
{
int y=fa[x],z=fa[y],id=wh(x);
ch[z][wh(y)]=x,fa[x]=z;
ch[y][id]=ch[x][id^1],fa[ch[x][id^1]]=y;
ch[x][id^1]=y,fa[y]=x;
}
void pushall(int x)
{
int p=x;
while(p)st[++top]=p,p=fa[p];
while(top>0)pushdown(st[top]),top--;
}
void splay(int &rt,int x)
{
pushall(x);
while(fa[x])
{
long long y=fa[x],z=fa[y];
if(z)
{
if(wh(x)==wh(y))rotate(y);
else rotate(x);
}
rotate(x);
}
rt=x;
}
int create(int &rt,int p,long long k,int id)
{
ch[p][id]=++cnt,val[cnt]=k,fa[cnt]=p,splay(rt,ch[p][id]);
return cnt;
}
int insert(int &rt,long long p)
{
int x=rt;
while(x)
{
pushdown(x);
if(val[x]==p)return x;
else if(p<val[x])
{
if(!ch[x][0])return create(rt,x,p,0);
x=ch[x][0];
}
else
{
if(!ch[x][1])return create(rt,x,p,1);
x=ch[x][1];
}
}
return x;
}
int getmin(int &rt)
{
int x=rt;
while(ch[x][0])pushdown(x),x=ch[x][0];
splay(rt,x);
return x;
}
int split(int &rt,long long k)
{
int x=rt,ap=0,pr=0;
long long ans=1e18;
while(x)
{
pr=x,pushdown(x);
if(k>=val[x])x=ch[x][1];
else if(k<val[x])
{
if(val[x]<=ans)ans=val[x],ap=x;
x=ch[x][0];
}
}
splay(rt,pr);
if(ap==0)
{
int nrt=rt;
rt=0;
return nrt;
}
splay(rt,ap);
int nrt=ch[rt][0];
fa[ch[rt][0]]=0,ch[rt][0]=0;
return nrt;
}
int merge(int &rt1,int &rt2)
{
bool flag=0;
while(rt1&&rt2)
{
if(!flag)
{
int p=getmin(rt1),nrt=0;
splay(rt1,p),nrt=split(rt2,val[p]),fa[nrt]=p,ch[p][0]=nrt;
}
else
{
int p=getmin(rt2),nrt=0;
splay(rt2,p),nrt=split(rt1,val[p]),fa[nrt]=p,ch[p][0]=nrt;
}
flag^=1;
}
return rt1+rt2;
}
int main()
{
val[1]=1e17;
n=read(),m=read();
for(int i=1;i<=n;i++)a[i]=read();
for(int i=1;i<=m;i++)ci=read(),li=read(),ri=read(),l[li].push_back(i),r[ri].push_back(i),c[li].push_back(ci);
for(int i=1;i<=n;i++)
{
for(int j=0;j<(int)l[i].size();j++)y[l[i][j]]=insert(rt,c[i][j]);
int nrt=split(rt,(a[i]-1)>>1);
rev[nrt]^=1,val[nrt]*=-1,ad[nrt]*=-1,swap(ch[nrt][0],ch[nrt][1]),val[nrt]+=a[i],ad[nrt]+=a[i];
rt=merge(rt,nrt);
for(int j=0;j<(int)r[i].size();j++)splay(rt,y[r[i][j]]),ans[r[i][j]]=val[y[r[i][j]]];
}
for(int i=1;i<=m;i++)print(ans[i]),putchar('\n');
return 0;
}
例题 \(6\) :
P5066 [Ynoi Easy Round 2014] 人人本着正义之名
考虑 \(3\sim 6\) 操作对序列的影响,通过简单模拟不难发现 \(3\sim 6\) 操作本质上就是让一段 \(0\) 或 \(1\) 的左右边界扩张或收缩一个位置。而 \(1,2\) 操作也可以转化为修改与覆盖区间相交的连续段的左右边界,再插入一个新的。\(7\) 操作就是先找出被完全包含的连续段,再加上左右相交的连续段分别统计贡献。需要特判被包含。
因此我们考虑维护 \(0\) 或 \(1\) 的极长连续段,用平衡树的节点维护连续段,每个节点维护子树内的和与这个连续段的左右端点与权值。
\(3\sim 6\) 操作需要考虑通过打区间左右扩张收缩懒标记实现。为了打懒标记时更新子树内信息,我们还需要记录子树内 \(0,1\) 的极长连续段个数。这样就可以通过偏移量乘上连续段个数更新子树信息。需要特判被包含。时间复杂度 \(O((n+m)\log(n+m))\)。
此时又出现了一个问题,可能会有一个连续段被不断收缩导致消失,此时不仅需要删除这个连续段,还需合并它前一个和后一个连续段。但每出现一次这种情况,就会使平衡树中减少两个节点。即使有覆盖操作,每次至多增加两个连续段。因此这种删除操作至多只会进行 \(n+m\) 次,每次在 FHQ 上找节点复杂度为 \(O(\log(n+m))\),因此不影响总时间复杂度。
实现上可以写两个分裂函数,一个按照小于等于 \(r\) 分裂,另一个按照小于 \(l\) 分裂,这样找完全不交区间比较容易。要特别注意各种操作中被完全包含的情况,需要特判。
删除被操作消失的区间时建议先把这些区间找出来,从小到大依次删除。不然这些消失的区间在平衡树里的位置很奇怪,有可能删除后加入的新区间在平衡树中的位置会出问题。
常数方面我的 Splay 比 FHQ-Treap 慢,因此我选用了 FHQ-Treap。比较显著的优化有 pushdown 的时候如果没有标记直接返回和按照讨论区的写法手写 FHQ-Treap 的随机函数。
#include <bits/stdc++.h>
using namespace std;
struct node
{
int l,r,key,val,sum,cl[2],mi[2],ldel[2],rdel[2];
}tr[8000000];
int n,m,op,l,r,a[3000001],ch[8000000][2],st[8000000],top=0,cnt=0,len=0,rt=0,la=0;
vector<int>lg,rg,vg,pl;
unsigned int rnd()
{
static unsigned int s=1;
return s*=19260817;
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
bool cmp(int x,int y)
{
return lg[x]<lg[y];
}
inline void pushup(int x)
{
tr[x].sum=tr[ch[x][0]].sum+tr[ch[x][1]].sum+(tr[x].r-tr[x].l+1)*tr[x].val;
tr[x].cl[tr[x].val]=tr[ch[x][0]].cl[tr[x].val]+tr[ch[x][1]].cl[tr[x].val]+1;
tr[x].cl[!tr[x].val]=tr[ch[x][0]].cl[!tr[x].val]+tr[ch[x][1]].cl[!tr[x].val];
tr[x].mi[tr[x].val]=min(tr[ch[x][0]].mi[tr[x].val],min(tr[ch[x][1]].mi[tr[x].val],tr[x].r-tr[x].l+1));
tr[x].mi[!tr[x].val]=min(tr[ch[x][0]].mi[!tr[x].val],tr[ch[x][1]].mi[!tr[x].val]);
}
inline void addtg(int x,int ldel[2],int rdel[2],int id)
{
tr[x].sum+=(rdel[1]+ldel[1])*tr[x].cl[1];
for(int i=0;i<=1;i++)
{
if(id)tr[x].ldel[i]+=ldel[i],tr[x].rdel[i]+=rdel[i];
tr[x].mi[i]+=(rdel[i]+ldel[i]);
}
tr[x].l-=ldel[tr[x].val],tr[x].r+=rdel[tr[x].val];
}
inline void pushdown(int x)
{
if(!(tr[x].ldel[0]||tr[x].ldel[1]||tr[x].rdel[0]||tr[x].rdel[1]))return;
if(ch[x][0])addtg(ch[x][0],tr[x].ldel,tr[x].rdel,1);
if(ch[x][1])addtg(ch[x][1],tr[x].ldel,tr[x].rdel,1);
tr[x].ldel[0]=tr[x].ldel[1]=tr[x].rdel[0]=tr[x].rdel[1]=0;
}
inline int create(int l,int r,int val)
{
int x=++cnt;
tr[x].l=l,tr[x].r=r,tr[x].val=val,tr[x].key=rnd(),pushup(x);
tr[x].ldel[0]=tr[x].ldel[1]=tr[x].rdel[0]=tr[x].rdel[1]=0;
return x;
}
inline int getmin(int x)
{
top=0,st[++top]=x,pushdown(x);
while(ch[x][0])x=ch[x][0],pushdown(x),st[++top]=x;
return x;
}
inline int getmax(int x)
{
top=0,st[++top]=x,pushdown(x);
while(ch[x][1])x=ch[x][1],pushdown(x),st[++top]=x;
return x;
}
inline void upall()
{
while(top)pushup(st[top]),top--;
}
void split(int p,int k,int &x,int &y,int id)
{
if(!p)x=y=0;
else
{
pushdown(p);
int q=tr[p].l+1;
if(id==1)q=tr[p].r;
if(q<=k)
{
x=p;
split(ch[x][1],k,ch[x][1],y,id);
}
else
{
y=p;
split(ch[y][0],k,x,ch[y][0],id);
}
pushup(p);
}
}
int merge(int x,int y)
{
if(!x||!y)return x+y;
pushdown(x),pushdown(y);
int rt=0;
if(tr[x].key>tr[y].key)ch[x][1]=merge(ch[x][1],y),rt=x;
else ch[y][0]=merge(x,ch[y][0]),rt=y;
pushup(rt);
return rt;
}
inline void insert(int l,int r,int k)
{
int x=0,y=create(l,r,k),z=0;
split(rt,r,x,z,1);
rt=merge(merge(x,y),z);
}
void dfs(int x,int &ll,int &rr)
{
pushdown(x);
ll=min(ll,tr[x].l),rr=max(rr,tr[x].r);
if(ch[x][0])dfs(ch[x][0],ll,rr);
if(ch[x][1])dfs(ch[x][1],ll,rr);
}
inline void erase(int &rt,int k,int id,int vd=0)
{
int x=0,y=0,z=0;
if(id==0)
{
split(rt,k,x,z,1),split(x,k-1,x,y,1);
y=merge(ch[y][0],ch[y][1]);
rt=merge(merge(x,y),z);
}
else
{
int ll=1e9,rr=0,vv=vd^1;
split(rt,k-1,x,y,1);
split(y,id+1,y,z,0);
dfs(y,ll,rr);
rt=merge(x,z);
if(ll<=rr)insert(ll,rr,vv);
}
}
inline void getpos(int x)
{
pushdown(x);
if(tr[x].r-tr[x].l+1<=0)lg.push_back(tr[x].l),rg.push_back(tr[x].r),vg.push_back(tr[x].val);
if(ch[x][0]&&min(tr[ch[x][0]].mi[0],tr[ch[x][0]].mi[1])<=0)getpos(ch[x][0]);
if(ch[x][1]&&min(tr[ch[x][1]].mi[0],tr[ch[x][1]].mi[1])<=0)getpos(ch[x][1]);
pushup(x);
}
void fix(int x)
{
lg.clear(),rg.clear(),vg.clear(),pl.clear(),getpos(x);
if(lg.size()==0)return;
for(int i=0;i<(int)lg.size();i++)pl.push_back(i);
sort(pl.begin(),pl.end(),cmp);
for(int i=0;i<(int)pl.size();i++)erase(rt,rg[pl[i]],lg[pl[i]],vg[pl[i]]);
}
inline void cover(int l,int r,int k)
{
int x=0,y=0,z=0,nl=0,nr=0;
split(rt,l,x,y,0),split(y,r,y,z,1);
nr=getmin(z);
if(nr&&tr[nr].l<=l)
{
if(tr[nr].val!=k)
{
int pr=tr[nr].r,pv=tr[nr].val;
tr[nr].r=l-1,upall();
rt=merge(merge(x,y),z);
insert(l,r,k),insert(r+1,pr,pv);
}
else rt=merge(merge(x,y),z);
return;
}
nl=getmax(x);
if(nl)
{
if(tr[nl].r>=r)
{
if(tr[nl].val!=k)
{
int pr=tr[nl].r,pv=tr[nl].val;
tr[nl].r=l-1,upall();
rt=merge(merge(x,y),z);
insert(l,r,k),insert(r+1,pr,pv);
}
else rt=merge(merge(x,y),z);
return;
}
if(tr[nl].val==k)l=tr[nl].l,erase(x,tr[nl].r,0);
else tr[nl].r=l-1,upall();
}
nr=getmin(z);
if(nr)
{
if(tr[nr].val==k)r=tr[nr].r,erase(z,tr[nr].r,0);
else tr[nr].l=r+1,upall();
}
if(!y)y=create(l,r,k);
else ch[y][0]=ch[y][1]=0,tr[y].l=l,tr[y].r=r,tr[y].val=k,pushup(y);
rt=merge(merge(x,y),z);
}
inline void shift(int l,int r,int ld0,int ld1,int rd0,int rd1)
{
int x=0,y=0,z=0,nl=0,nr=0;
split(rt,l+1,x,y,0),split(y,r-1,y,z,1);
int ld[2]={ld0,ld1},rd[2]={rd0,rd1};
nr=getmin(z);
if(nr&&tr[nr].l<=l)
{
rt=merge(merge(x,y),z);
return;
}
nl=getmax(x);
if(nl&&tr[nl].r>=l)
{
if(tr[nl].r>=r)
{
rt=merge(merge(x,y),z);
return;
}
if(tr[nl].val==0&&rd[0])ld[0]=ld[1]=rd[1]=0,addtg(nl,ld,rd,0),upall(),ld[0]=ld0,ld[1]=ld1,rd[0]=rd0,rd[1]=rd1;
if(tr[nl].val==1&&rd[1])ld[0]=ld[1]=rd[0]=0,addtg(nl,ld,rd,0),upall(),ld[0]=ld0,ld[1]=ld1,rd[0]=rd0,rd[1]=rd1;
}
if(y)addtg(y,ld,rd,1);
nr=getmin(z);
if(nr&&tr[nr].l<=r)
{
if(tr[nr].val==0&&ld[0])rd[0]=rd[1]=ld[1]=0,addtg(nr,ld,rd,0),upall(),ld[0]=ld0,ld[1]=ld1,rd[0]=rd0,rd[1]=rd1;
if(tr[nr].val==1&&ld[1])rd[0]=rd[1]=ld[0]=0,addtg(nr,ld,rd,0),upall();
}
rt=merge(merge(x,y),z);
}
inline int query(int l,int r)
{
int x=0,y=0,z=0,now=0,ans=0;
split(rt,l,x,y,0),split(y,r,y,z,1),ans=tr[y].sum;
now=getmax(x);
if(now&&tr[now].r>=r)
{
rt=merge(merge(x,y),z);
return tr[now].val*(r-l+1);
}
if(now&&tr[now].val)ans+=(tr[now].r-l+1);
now=getmin(z);
if(now&&tr[now].l<=l)
{
rt=merge(merge(x,y),z);
return tr[now].val*(r-l+1);
}
if(now&&tr[now].val)ans+=(r-tr[now].l+1);
rt=merge(merge(x,y),z);
return ans;
}
int main()
{
tr[0].sum=tr[0].cl[0]=tr[0].cl[1]=0,tr[0].mi[0]=tr[0].mi[1]=1e9;
n=read(),m=read();
for(int i=1;i<=n;i++)
{
a[i]=read();
if(i==1)len=1;
else if(a[i]!=a[i-1])insert(i-len,i-1,a[i-1]),len=1;
else len++;
}
insert(n-len+1,n,a[n]);
for(int i=1;i<=m;i++)
{
op=read(),l=read(),r=read();
l^=la,r^=la;
if(l>r)swap(l,r);
if(op==1)cover(l,r,0);
else if(op==2)cover(l,r,1);
else if(op==3)shift(l,r,0,1,-1,0);
else if(op==4)shift(l,r,-1,0,0,1);
else if(op==5)shift(l,r,1,0,0,-1);
else if(op==6)shift(l,r,0,-1,1,0);
else if(op==7)la=query(l,r),printf("%d\n",la);
fix(rt);
}
return 0;
}
后记
这篇学习笔记成功取代 【6】线段树学习笔记,共 \(1757\) 行,成为最长的学习笔记。
讲个笑话:整理这篇学习笔记之前,我发现我的平衡树例题只有两道板子题。
作为机房唯一的 Splay 党,在天天与万恶的 FHQ 党人斗争的过程中,我对 Splay 的认知更加深入。我与 Splay 共存亡!
何以曾经夜深梦闲人 迟迟不梦君
如今病减诗情 睡去未必醒
九百行诗往来频寄信 愈病愈苦吟
百年之后 惟恐不能倾



 浙公网安备 33010602011771号
浙公网安备 33010602011771号