强化学习（三）：动态规划

Dynamic Programming

DP指的是一套算法集，这样的算法集在环境模型是一种马尔可夫决策过程且已知的情况下，可以用于计算得到最优的决策。由于要求已知完美的模型且计算量极大，DP的实用性不强，但其理论意义是很重要的。因为在强化学习后面接触的算法都是企图克服完美模型假定与大量计算并得到与DP同样的结果。

通常，在DP算法中，假定环境是一个有限的马尔可夫过程。DP的关键想法甚至强化学习的关键想法即是通过价值函数来组织或框定对优良决策的搜索。

根据Bellman方程，可知：

\[v_{*}(s) = \max_{a}E [R_{t+1} + \gamma v_*(S_{t+1})| S_t = s, A_t = a] = max_a\sum_{s',r}p(s',r|s,a)[r + \gamma v_*(s')] \]

\[q_{*}(s,a) = E[R_{t+1} + \gamma\max_{a'}q_*(S_{t+1}, a')| S_t = s, A_t = a] = \sum_{s',r}p(s',r|s,a)[r+\gamma\max_{a'}q_*(s',a')] \]

DP是用一种迭代更新的方式去逼近真实的价值函数。

Policy Evaluation (Prediction)

预测问题即是对于任意的决策策略，计算状态－价值函数(state-value)函数\(v_{\pi}\):

\[v_{k+1}(s) \dot = E_{\pi} [G_t| S_t = s] = E_{\pi}[R_[t+1]+\gamma G_{t+1}|S_t = s] = \sum_{a}\pi(a|s)\sum_{s',r}p(s',r|s,a)[r + \gamma v_k(s')] \]

当\(k \rightarrow \infty\)时，\(v_k\)收敛于真实的\(v_{\pi}\)。这种方式被称为迭代策略评估。

Input pi, the policy to be evaluated
Algorithm parameter: a small threshold theta >0 determining accuracy of estimation
Initialize V(s), for all s in S_plus(terminal stated included), arbitarily execept that v(terminal) = 0
while True: 
 delta = 0
 for s in S_plus:
 	 v = V(s)
 	 V(s) = sum_a pi(a|s)sum_{s',r}p(s',r|s,a)[r+gamma V(s')]
 	 delta = max(delta, |v-V(s)|)
 	 if delta < theta
 	 	 break

Policy Improvement

policy improvement theorem:

all s in S:

\[q_{\pi}(s, \pi'(s)) \ge v_{\pi}(s) \rightarrow v_{\pi'}(s) \ge v_{\pi}(s) \]

Policy Iteration

\[\pi_0 \xrightarrow{\quad E\quad }v_{\pi_0} \xrightarrow{\quad I\quad } \pi_1 \xrightarrow{\quad E\quad }v_{\pi_1}\xrightarrow{\quad I\quad }\pi_2\xrightarrow{\quad E\quad } ... \xrightarrow{\quad I\quad }\pi_* \xrightarrow{\quad E\quad }v_* \]

# Initialzation
V(s), pi(s)

#Policy Evaluation
while True:
    delta = 0
    for s in S:
        v = V(s)
        V(s) = sum_{s',r}p(s',r|s,pi(s))[r+gamma(V(s'))]
        delta = max(delta, |v- V(s)|)
    if delta < theta:
        break
                                                   
#policy improvement
policy_stable = True
for s in S:
    action = pi(s)
    pi(s) = argmax_a sum_{s',r}p(s',r|s,a)[r+gammaV(s')]
    if action != pi(s):
        policy_stable = False
if policy_stable:
    return v*, pi*
else:
    go to policy evaluation
      

Value Iteration

上面策略迭代算法的劣势，显而易见，每一步的迭代都要进行策略评估，即对所有的状态都要扫描一遍。

下面的价值迭代算法对策略迭代进行了优化：

\[v_{k+1}(s) \dot = \max_{a} E [ R_{t+1}+ \gamma v_k(S_{t+1})| S_t = s, A_t = a] = \max_{a}\sum_{s',r}p(s',r|s,a)[r + \gamma　v_k(s')] \]

Algorithm parameter: a small threshold theta determining accuracy of estimation
Initialize V(s), for all s in S_plus, arbitrarily except that V(terminal) = 0

while True:
    delta = 0
    for s in S:
        v = V(s)
        V(s) = max_a sum_{s',r}p(s',r|s,a)[r+gamma v(s')]
        delta = max(delta, |v - V(s)|)
    if delta <theta:
        pi(s) = argmax_a sum_{s',r}p(s',r|s,a)[r + gamma V(s')]
        break

Generalized Policy Iteration

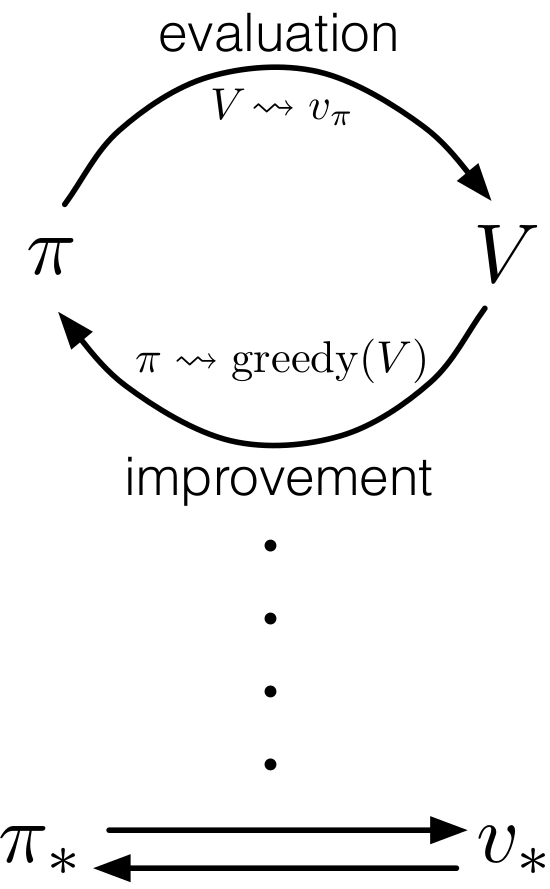
策略迭代由两个同时发生并相互作用的过程组成，一个是策略评估，即让价值函数与当前的策略相一致，或者说在当前策略下找到与其对应的价值函数。另一个就是策略提升，即在当前价值函数的前提下，通过贪婪的方式找到最优策略。GPI指的是这样的通用想法：让策略评估（ＰＥ）与策略提升（ＰＩ）的交互　独立于两过程的各自己过程细节。