有向图

有向图

有向图（Directed Graph）是一种图结构，其中的边（连接节点的线）具有方向性。这意味着每条边都有一个起始节点和一个结束节点，表示从一个节点指向另一个节点。

有向图的特点

1. 方向性：边的方向指示了节点之间的关系。例如，如果有一条边从节点 A 指向节点 B，表示 A 到 B 的关系，但不一定表示 B 到 A 的关系。
2. 表示方式：
   • 邻接矩阵：使用二维数组表示节点之间的连接关系。
   • 邻接列表：使用列表或集合表示每个节点的直接邻居。
3. 节点和边：
   • 节点（Vertex）：图中的元素，通常表示为点。
   • 边（Edge）：连接节点的线，表示节点之间的关系。
4. 示例：
   • 社交网络中的关注关系（用户 A 关注用户 B，但 B 不一定关注 A）。
   • 网络流量中的路由（数据包从源节点发送到目标节点）。

实际情况中，有向图中可能有复杂的依赖关系，包括：

• 线性依赖：A→B→C
• 分支依赖：A→B, A→C
• 汇聚依赖：B→D, C→D
• 循环依赖：A→B→C→A（形成环）

实际案例

给定输入，输入的形式为一组任务依赖关系：例如 1->2表示id为1的任务依赖于id为2的任务

1->2,1->3,1->4,2->3,3->6,3->7,3->4,5->1,6->5,8->6,8->2

使用邻接表来表示：

1: [2, 3, 4]
2: [3]
3: [6, 7, 4]
5: [1]
6: [5]
8: [6, 2]

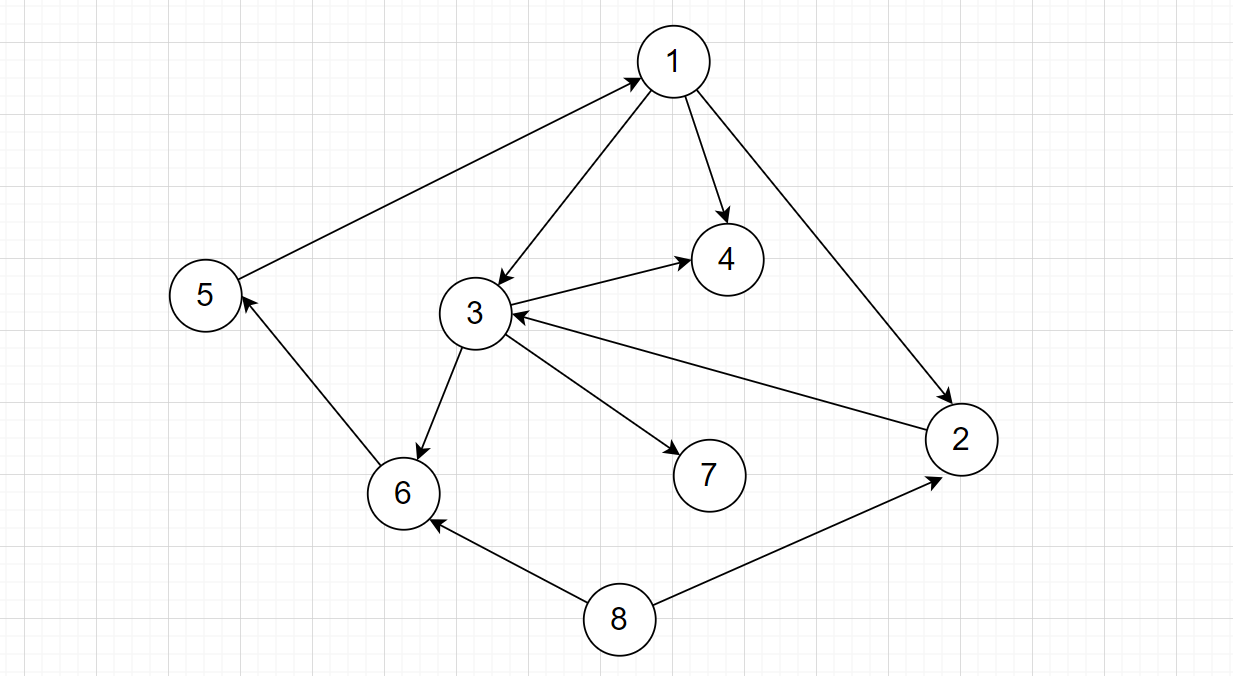
这个图长下面这个样子：

输入处理

// 表示每个依赖关系
public class Task {
    Long taskId; 			// 任务ID
    Long inputTaskId; 		// 依赖的任务ID
}

/**
 * 处理输入
 */
public static List<Task> parseDependencies(String[] dependencyStrings) {
    List<Task> tasks = new ArrayList<>();
    for (String depStr : dependencyStrings) {
        String[] split = depStr.split("->");
        tasks.add(new Task(Long.parseLong(split[0]), Long.parseLong(split[1])));

    }
    return tasks;
}

/**
 * 构建邻接表表示的图
 */
private static Map<Long, List<Long>> buildGraph(List<Task> tasks) {
    Map<Long, List<Long>> graph = new HashMap<>();
    for (Task task : tasks) {
        graph.putIfAbsent(task.getTaskId(), new ArrayList<>());
        if (task.getInputTaskId() != null) {
            graph.get(task.getTaskId()).add(task.getInputTaskId());
        }
    }
    return graph;
}

检测是否成环

使用深度优先搜索(DFS)检测图中是否存在环。时间复杂度：O(V+E)，V是顶点数，E是边数

public static void main(String[] args) {
    String input = "1->2,1->3,1->4,2->3,3->6,3->7,3->4,5->1,6->5,8->6,8->2";
    List<Task> tasks = parseDependencies(input.split(","));
    Map<Long, List<Long>> graph = buildGraph(tasks);

    // 检测是否存在环
    boolean hasCycle = false;
    Set<Long> visited = new HashSet<>();
    Set<Long> currentPath = new HashSet<>();

    for (Long startNode : graph.keySet()) {
        hasCycle = dfs(graph, startNode, visited, currentPath);
        if (hasCycle) {
            System.out.println("图中存在环！");
            break;
        }
    }
    if (!hasCycle) {
        System.out.println("图中不存在环。");
    }
}

/**
 * 执行深度优先搜索，检测图中是否存在环。
 *
 * @param graph      图，表示为节点及其邻居的映射。
 * @param node       当前正在访问的节点。
 * @param visited    已访问节点的集合。
 * @param currentPath 当前路径中的节点集合，用于检测环。
 * @return 如果图中存在环，则返回 true；否则返回 false。
 */
private static boolean dfs(Map<Long, List<Long>> graph, Long node, 
                           Set<Long> visited, Set<Long> currentPath) {
    // 检查当前路径是否已包含该节点
    if (currentPath.contains(node)) {
        return true; // 发现环，返回 true
    }

    // 如果节点已访问过，返回 false
    if (visited.contains(node)) {
        return false;
    }

    // 标记节点为已访问和当前路径中的节点
    visited.add(node);
    currentPath.add(node);
    boolean hasCycle = false; // 标记是否存在环
    // 遍历邻居
    if (graph.containsKey(node)) {
        for (Long neighbor : graph.get(node)) {
            hasCycle = dfs(graph, neighbor, visited, currentPath);
            if (hasCycle) {
                break; // 如果发现环，停止探索
            }
        }
    }
    // 回溯
    currentPath.remove(node); // 从当前路径中移除节点
    return hasCycle; // 返回是否存在环
}

非递归写法：分别使用栈和不使用栈两种方式

public static void main(String[] args) {
    String input = "1->2,1->3,1->4,2->3,3->6,3->7,3->4,5->1,6->5,8->6,8->2";
    List<Task> tasks = parseDependencies(input.split(","));
    Map<Long, List<Long>> graph = buildGraph(tasks);
    // 检测是否存在环
    boolean hasCycle = false;
    Set<Long> visited = new HashSet<>();
    Set<Long> currentPath = new HashSet<>();

    for (Long startNode : graph.keySet()) {
        if (!visited.contains(startNode)) {
            hasCycle = hasCycle(graph, startNode, visited);
            // 或者: hasCycle = hasCycle(graph, startNode, visited, currentPath);
            if (hasCycle) {
                System.out.println("图中存在环！");
                break;
            }
        }
    }
    if (!hasCycle) System.out.println("图中不存在环。");
}

private static boolean hasCycle(Map<Long, List<Long>> graph, Long start, Set<Long> visited) {
    Set<Long> currentPath = new HashSet<>(); // 当前路径中的节点
    Stack<Long> stack = new Stack<>();
    stack.push(start);
    while (!stack.isEmpty()) {
        Long node = stack.pop();
        if (currentPath.contains(node)) {
            return true; // 发现环，返回 true
        }
        if (!visited.contains(node)) {
            visited.add(node);
            currentPath.add(node);
            // 将邻节点压入栈
            if (graph.containsKey(node)) {
                for (Long neighbor : graph.get(node)) {
                    stack.push(neighbor);
                }
            }
        }
        // 从当前路径中移除节点
        currentPath.remove(node);
    }
    return false; // 没有发现环
}

/**
 * 迭代实现的深度优先搜索，检测图中是否存在环。
 *
 * @param graph       图，表示为节点及其邻居的映射。
 * @param start       开始节点。
 * @param visited     已访问节点的集合。
 * @param currentPath 正在访问节点的集合。
 * @return 如果图中存在环，则返回 true；否则返回 false。
 */
private static boolean hasCycle(Map<Long, List<Long>> graph, Long start, 
                                Set<Long> visited, Set<Long> currentPath) {
    // 使用状态来标记节点状态
    Map<Long, Integer> state = new HashMap<>();

    for (Long node : graph.keySet()) {
        state.put(node, 0); // 0: 未访问, 1: 正在访问, 2: 已访问
    }

    // 进行迭代 DFS
    state.put(start, 1); // 标记为正在访问
    currentPath.add(start);

    while (!currentPath.isEmpty()) {
        Long node = currentPath.iterator().next(); // 获取当前路径中的第一个节点

        if (graph.containsKey(node)) {
            boolean hasCycle = false;

            for (Long neighbor : graph.get(node)) {
                if (state.get(neighbor) == 1) {
                    return true; // 发现环，返回 true
                }

                if (state.get(neighbor) == 0) {
                    state.put(neighbor, 1); // 标记为正在访问
                    currentPath.add(neighbor); // 添加到当前路径
                }
            }
        }

        // 完成对当前节点的处理
        state.put(node, 2); // 标记为已访问
        currentPath.remove(node); // 从当前路径中移除
    }

    return false; // 没有发现环
}

查找所有路径

找到所有路径的方法

1. 从每个节点开始，采用深度优先搜索（DFS）。

2. 记录当前路径，当到达没有出边的节点时，保存该路径。

下面是一个示例：

public static void main(String[] args) {
    String input = "1->2,1->3,1->4,2->3,3->6,3->7,3->4,5->1,6->5,8->6,8->2";
    List<Task> tasks = parseDependencies(input.split(","));
    Map<Long, List<Long>> graph = buildGraph(tasks);
    // 查找所有路径
    List<List<Long>> allPaths = new ArrayList<>();
    for (Long startNode : graph.keySet()) {
        dfs(graph, startNode, new ArrayList<>(), new HashSet<>(), allPaths);
    }
    // 输出所有路径
    for (List<Long> path : allPaths) {
        System.out.println(path);
    }
}

/**
 * 深度优先搜索，从给定节点查找所有路径。
 *
 * @param graph     图
 * @param node      当前正在访问的节点
 * @param path      当前构建的路径
 * @param visited   已访问节点的集合，用于检测环，防止无限循环
 * @param allPaths  存储所有找到的路径的列表
 */
private static void dfs(Map<Long, List<Long>> graph, Long node, List<Long> path, 
                        Set<Long> visited, List<List<Long>> allPaths) {
    // 检查是否已在当前路径中
    if (visited.contains(node)) {
        return; // 发现环，停止探索
    }
    visited.add(node);
    path.add(node);
    if (!graph.containsKey(node)) { // 如果没有出边，保存路径
        allPaths.add(new ArrayList<>(path));
    } else {
        for (Long neighbor : graph.get(node)) {
            dfs(graph, neighbor, path, visited, allPaths);
        }
    }
    // 回溯
    path.remove(path.size() - 1);
    // 移除当前节点的访问标记，以便其他路径可以继续探索
    visited.remove(node);
}

关键点说明

1. 路径查找算法：使用深度优先搜索(DFS)遍历所有可能的路径
2. 环处理：当检测到节点已在当前路径中时，识别为环并停止该路径的继续探索
3. 起点选择：优先从没有入边的节点开始查找（如果有）
4. 终止条件：当节点没有出边时，路径终止
5. 通过visited集合防止无限循环
6. 循环路径会被截断（不包含完整循环）
7. 回溯：在回溯时，移除当前节点的访问标记，以便其他路径可以继续探索。

扩展功能

针对其他场景，可以在之前的基础上做一些改动

• 可以添加最大长度限制
• 可以过滤包含特定节点的路径
• 并行处理：不同起点的DFS可以并行执行