数学公式的几何意义（初等数学）

三角函数的图像

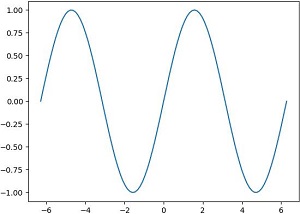
y=sinx,x∈[2kπ,2(k+1)π,k∈Z且k≠0]

from matplotlib import pyplot as plt
import numpy as np

x=np.linspace(-2*np.pi,2*np.pi,100)
y=np.sin(x)

plt.plot(x,y)
plt.show()

>>

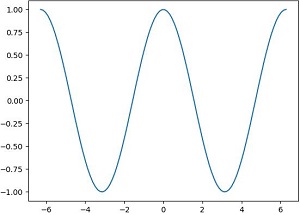
由y=cosx=sin(x+π/2)—>y=cosx的图像为y=sinx向左平移π/2个单位长度

from matplotlib import pyplot as plt
import numpy as np

x=np.linspace(-2*np.pi,2*np.pi,100)
y=np.cos(x)
plt.plot(x,y)
plt.show()

>>

~《人教版高二数学必修四(2004A版)》p31，32

圆的极坐标方程

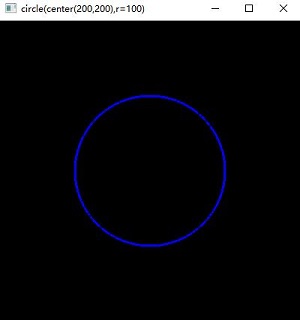
x=a+r*cosθ，y=b+r*sinθ

import numpy as np
import cv2 as cv
img=np.zeros((400,400,3),np.uint8) 

a,b=(200,200)
r=100
theta=np.arange(0,2*np.pi,0.01)
x=a+r*np.cos(theta)
y=b+r*np.sin(theta)

i=0
while i<len(theta):
    cv.circle(img, (int(x[i]),int(y[i])), 1, (255,0,0), 0)
    i+=1
    
cv.imshow("circle(center(200,200),r=100)",img)

>>

向量的几何意义
向量的数学定义就是一个数字列表，一个向量就是一个数组。从几何意义上说，向量是有大小和方向的有向线段。
·向量的大小就是向量的长度（模）。向量有非负的长度。
·向量的方向描述了空间中向量的指向。注意，方向并不完全和方位等同。

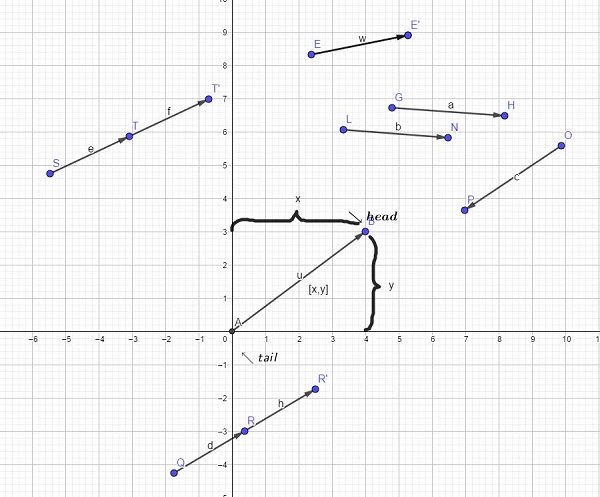
2维向量的表示

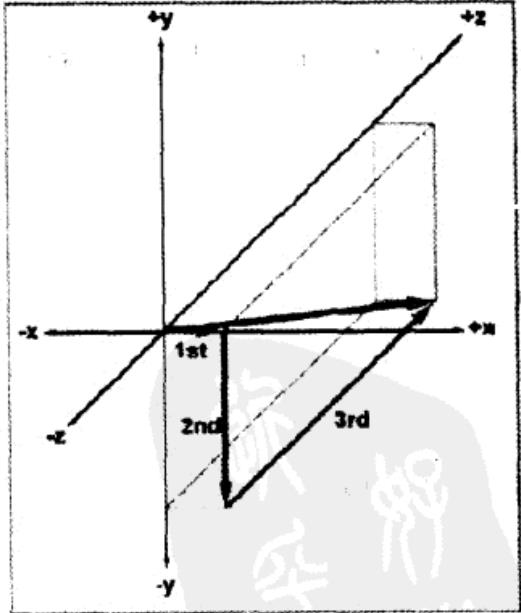
3维向量的表示

-向量模运算

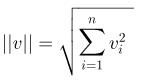
·向量的其他运算

~《3D数学基础：图形与游戏开发》

~猎豹网校《3D数学基础：图形与游戏开发》视频教程