Stochastic Gradient Descent
一、从Multinomial Logistic模型说起
1、Multinomial Logistic
令为
维输入向量;
为输出label;(一共k类);
为模型参数向量;
Multinomial Logistic模型是指下面这种形式:
其中:
例如:时,输出label为0和1,有:
2、Maximum Likelihood Estimate and Maximum a Posteriori Estimate
(1)、Maximum Likelihood Estimate
假设有数据集,为了训练一个模型通常使用极大似然法来确定模型参数:
(2)、Maximum a Posteriori Estimate
假设模型参数的分布服从
,那么在给定数据集上我们想要找到的最佳参数满足以下关系:
利用上面的式子可以定义求解该问题的损失函数:
个人认为,从统计学习的角度来说,上面式子第一部分描述了偏差(经验风险),而第二部分描述了方差(置信风险)。
3、L1-regularized model and L2-regularized model
对模型参数的分布
,可以有下面的假设:
(1)、Gaussian Prior
(2)、Laplace Prior
当时,叫做L2-regularized:
当时,叫做L1-regularized:
在这里常数是一个用来调节偏差与方差的调节因子:
●很小时,强调likelihood,此时会造成Overfit;
●很大时,强调regularization,此时会造成Underfit。
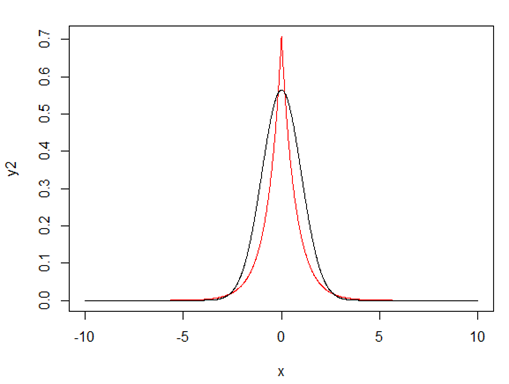
在相同的条件下,Gaussian Prior和Laplace Prior的比较如下:
图1 - 红色为Laplace Prior,黑色为Gaussian Prior
4、L1-regularized model ?or L2-regularized model?
目前主流的方法都选择用L1-regularized,包括各种L-BFGS(如:OWL-QN)和各种SGD方法,主要原因如下:
●我们要优化的目标是:
从图1可以看出,要想让取得最大值,权重向量需要靠近其mean值(也就是0),显然服从Laplace Prior的权重向量下降速度要快于服从Gaussian Prior的;
●以时的梯度下降算法为例,权重
的更新方式如下:
○ Gaussian Prior:
○ Laplace Prior:
当时,
;
当时,
。
当与
同号时表明没有误分,权重的绝对值会以一个比较小的速度更新,而当
与
异号时误分发生,权重的绝对值会以一个比较大的速度更新。
●将权重更新看成两个阶段:likelihood + regularization,暂时不考虑likelihood,那么k次迭代后有下面关系:
○ Gaussian Prior:
○ Laplace Prior:
当时,
;
当时,
。
当,虽然前者的极限值为0,但是不会精确为0,而后者每次更新一个常数,这就意味着理论上后者可能会精确的将权重更新为0。
●L1-regularized能够获得稀疏的feature,因此模型训练过程同时在进行feature selection。
●如果输入向量是稀疏的,那么Laplace Prior能保证其梯度也是稀疏的。
二、L1-Stochastic Gradient Descent
1、Naive Stochastic Gradient Descent
随机梯度下降算法的原理是用随机选取的Training Set的子集来估计目标函数的梯度值,极端情况是选取的子集只包含一条Sample,下面就以这种情况为例,其权重更新方式为:
这种更新方式的缺点如下:
●每次迭代更新都需要对每个feature进行L1惩罚,包括那些value为0的没有用到的feature;
●实际当中在迭代时能正好把权重值更新为0的概率很小,这就意味着很多feature依然会非0。
2、Lazy Stochastic Gradient Descent
针对以上问题,Carpenter在其论文《Lazy Sparse Stochastic Gradient Descent for Regularized Mutlinomial Logistic Regression》(2008)一文中进行了有效的改进,权重更新采用以下方式:
这种更新方式的优点如下:
●通过这样的截断处理,使得惩罚项不会改变函数值符号方向,同时也使得0权重能够自然而然地出现;
●算法中使用lazy fashion,对那些value为0的feature不予更新,从而加快了训练速度。
这种方式的缺点:
●由于采用比较粗放的方式估计真实梯度,会出现权重更新的波动问题,如下图:
3、Stochastic Gradient Descent with Cumulative Penalty
这个方法来源于Yoshimasa Tsuruoka、Jun’ichi Tsujii和 Sophia Ananiadou的《Stochastic Gradient Descent Training for L1-regularized Log-linear Models with
Cumulative Penalty》(2009)一文,其权重更新方法如下:
其中:
,表示每个权重在第k次迭代时,理论上能够得到的累积惩罚值;
,表示当前权重已经得到的累加惩罚值。
算法描述如下:
关于学习率的确定,传统的方法是:
, 其中k为第k次迭代
这种方法在实际当中的收敛速度不太理想,这篇论文提出以下方法:
, 其中k为第k次迭代
在实际当中表现更好,但要注意在理论上它不能保证最终的收敛性,不过实际当中都有最大迭代次数的限制,因此这不是什么大问题。
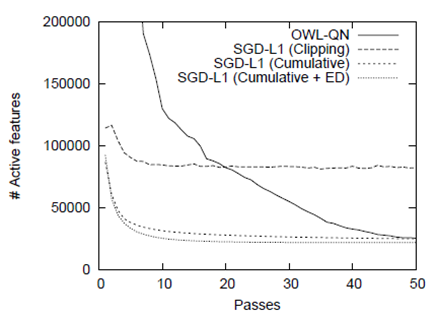
与Galen Andrew and Jianfeng Gao的《 Scalable training of L1-regularized log-linear models》(2007)提出的OWL-QN方法相比较如下:
4、Online Stochastic Gradient Descent
由于L1-regularized权重迭代更新项为常数,与权重无关,因此以N为单位批量更新Sample一次的效果和每次更新一个Sample一共更新N次的效果是一样一样的,因此采用这种方法只用在内存中存储一个Sample和模型相关参数即可。
5、Parallelized Stochastic Gradient Descent
Martin A. Zinkevich、Markus Weimer、Alex Smola and Lihong Li.在《Parallelized Stochastic Gradient Descent》一文中描述了简单而又直观的并行化方法:
以及
下一步考虑把这个算法在Spark上实现试试,还得用时实践来检验的。
三、参考资料
1、Galen Andrew and Jianfeng Gao. 2007. 《Scalable training of L1-regularized log-linear models》. In Proceedings of ICML, pages 33–40.
2、Bob Carpenter. 2008.《 Lazy sparse stochastic gradient descent for regularized multinomial logistic regression》.Technical report, Alias-i.
3、Martin A. Zinkevich、Markus Weimer、Alex Smola and Lihong Li. 《Parallelized Stochastic Gradient Descent》.Yahoo! Labs
4、John Langford, Lihong Li, and Tong Zhang. 2009. 《Sparse online learning via truncated gradient》. The Journal of Machine Learning Research (JMLR), 10:777–801.
5、Charles Elkan.2012.《Maximum Likelihood, Logistic Regression,and Stochastic Gradient Training》.
四、相关开源软件
1、wapiti:http://wapiti.limsi.fr/
2、sgd2.0:http://mloss.org/revision/view/842/
3、 scikit-learn:http://scikit-learn.org/stable/
4、 Vowpal Wabbit:http://hunch.net/~vw/
5、deeplearning:http://deeplearning.net/
6、LingPipe:http://alias-i.com/lingpipe/index.html










 浙公网安备 33010602011771号
浙公网安备 33010602011771号