SVM学习——线性学习器
变量之间存在的一次函数关系是线性关系,那么线性分类就应该是利用这样一种线性关系将输入学习器的样例按照其标记分开。一个线性函数的因变量值是连续的,而分类问题则一般是离散的,这个实值函数可以这样表示:
其中
是权重向量,
是阈值参数,由
可以确定一个超平面。
假设,当时,输入样本
标记为正类,否则为负类,这里的
为阈值,相当于这里有一个决策规则
,从几何上说,
定义的超平面(
维欧氏空间中维度大于一的线性子空间)将输入空间分成了两部分,分别对应于两个类别标记,
决定了超平面距离原点的距离,
决定了超平面的方向和大小,如图:
很明显,这个分类超平面不是唯一的(当然,如果超平面不存在则输入空间线性不可分),只要输入集合确定,那么实际上它的分布也就确定了,如果这个分类超平面客观上存在,那么直观地看,任意一个数据样例离超平面越远则说明这个超平面把数据分的越“开”,于是就有了函数间隔的定义:
定义1:输入样本对应于超平面
的函数间隔是:
,这里
是数据分类标记,不失一般性可取值为-1表示负类和+1表示正类,如果
则意味着数据被正确分类(不管是负类还是正类,如果实际输出和目标输出同号则意味着它们的乘积大于0,否则表明本来为负类的被分成了正类或者本来为正类的分成了负类,所以乘积为负)。显然,输入样本集合到超平面的函数距离由离超平面最近的样例决定。
将上式转化为归一化线性函数:,得到的量叫做几何间隔,回想空间中点到直线的距离公式:设直线方程为:
,则点
到直线的距离为:
,这里的就是向量
的2-范数,所以几何间隔可以看作是输入样本到分类超平面的距离。
可以通过下图理解几何间隔:
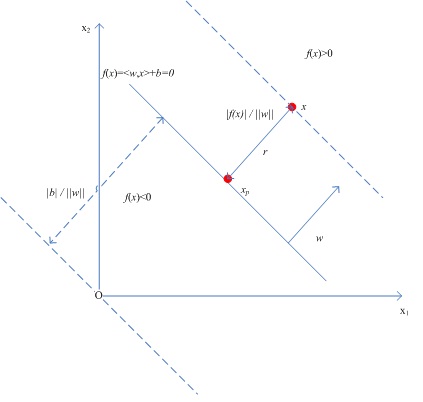
对于任意点,在分类超平面
上的投影点位
,
为点
到分类超平面的距离,显然有:
(为w的单位方向向量),于是有:
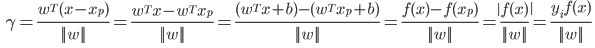 。
。
回想Rosenblatt感知器的原始形式:
--------------------------------------------begin 感知器算法------------------------------------------------
已知线性可分的数据集合S,其势为n,学习率为,则
while (!所有样例都被正确分类){
foreach(i in 1..n){
if ()
{
}
}
}
---------------------------------------------end 感知器算法-------------------------------------------------
当表明当前输入样本被误分了,因此权重被更新了多少次就表明样本被误分了多少次,
假设存在向量满足
,对任意一个输入样本都有
,
是一个固定的值,这就意味着所有输入样本和由
和
决定的超平面之间的最小几何间隔为
,那么找到这个超平面前S中的样本最多会被误分多少次呢?
-----------------------------------------begin 线性分类器分类误差上界推导-----------------------------------
构造新的输入样本向量,和权重向量
,一旦发生分类错误,则有:
,
于是,
(式子1);
3、从R的定义可以发现它其实描述了输入样本分布的广泛程度,对于由和
决定的超平面,
描述了超平面离原点的距离,因此这个距离一定是小于等于R的,于是有
(式子3);
4、由柯西-许瓦茨不等式可以得到:(式子4)。
最后,由式子1、式子2、式子3和式子4,可以得到以下关系:
这个式子很重要,它从理论上证明了如果分类超平面存在,则对于输入样本S,在有限次迭代和最多次分类错误下就可以找到这个分类超平面,输入样本一旦确定,R也就确定了,这意味着此时
只和几何间隔
有关且为反比关系。
---------------------------------------------end 线性分类器分类误差上界推导---------------------------------
回到函数间隔和几何间隔
这两个量,对分类超平面做尺度变换(类似于
),发现这个变换并不会使与原有超平面
相关联的函数关系发生变化,当用几何间隔来评价分类器的分类性能时,由于归一化而使这种尺度变换对评价不产生影响,因此完全可以将函数间隔固定为1,那么,对于正例有:
,对于负例有:
,于是正例或者负例与分类超平面之间的几何间隔为:
。
于是,最大化几何间隔就变成了最小化,等价于最小化
,最后得到下面的最优化问题:
------------------------------------------------begin --------------------------------------------------------
对于给定的样本集合
求最优化问题
------------------------------------------------end --------------------------------------------------------
求解上面的问题就要用到最优化理论中的一些方法了,下一篇正好复习一下。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号