LocalParameterization子类说明：QuaternionParameterization类和EigenQuaternionParameterization类

简单地说。LocalParameterization 是在优化 Manifold 上的变量时需要考虑的，Manifold 上变量是 over parameterized，即 Manifold 上变量的维度大于其自由度。这会导致 Manifold 上变量各个量之间存在约束，如果直接对这些量求导、优化，那么这就是一个有约束的优化，实现困难。为了解决这个问题，在数学上是对 Manifold 在当前变量值处形成的切空间（Tangent Space）求导，在切空间上优化，最后投影回 Manifold。

对于 SLAM 问题，广泛遇到的 Manifold 是旋转，旋转仅需使用 3 个量（so(3)）即可表达，但是实际应用中因为涉及到万向锁的问题，在更高维度表达旋转。四元数就是在维度 4 表达 3 个自由度的三维空间的旋转。

目录

• 1.四元数相关知识
  • 1.1 四元数乘法
• 2.QuaternionParameterization
  • 2.1 QuaternionParameterization::Plus
  • 2.2 QuaternionParameterization::ComputeJacobian
• 3.EigenQuaternionParameterization
  • 3.1 EigenQuaternionParameterization::Plus
  • 3.2 EigenQuaternionParameterization::ComputeJacobian

1.四元数相关知识

1.1 四元数乘法

对于两个四元数

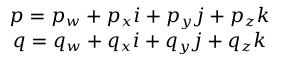
得到pq的乘法为

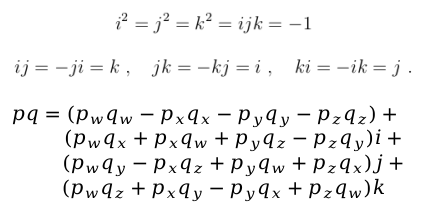
Ceres 中四元数通常采用的内存布局为 w, x, y, z，pq乘法写成4×1矩阵，如下

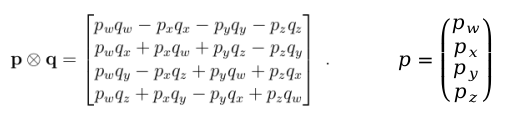
可以推导出如下公式

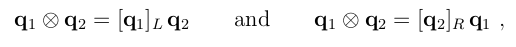
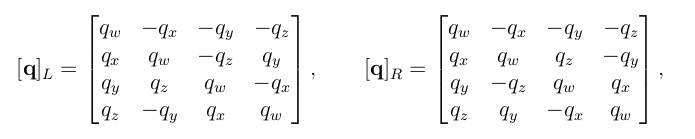
但是Eigen::Quaternion，其内部内存分布为：x, y, z, w 和 Ceres 存储的顺序不同 （w, x, y, z），因此乘法公式写为

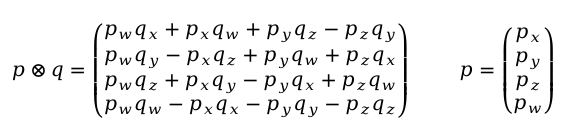
可以推导出如下公式

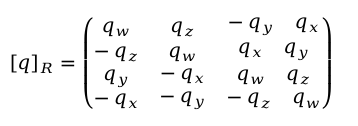
2.QuaternionParameterization

class CERES_EXPORT QuaternionParameterization : public LocalParameterization {
 public:
  virtual ~QuaternionParameterization() {}

  // 重载的 Plus 函数给出了四元数的更新方法，接受参数分别为优化前的四元数 x，用旋转矢量表示的增量delta，以及更新后的四元数 x_plus_delta
  // 函数首先将增量由旋转矢量转换为四元数，随后采用标准四元数乘法对四元数进行更新
  virtual bool Plus(const double* x,
                    const double* delta,
                    double* x_plus_delta) const;

  // 四元数相对于旋转矢量的雅克比矩阵。即x_plus_delta( Plus(x, delta) ) 关于 delta( delta接近0 )的雅克比矩阵
  virtual bool ComputeJacobian(const double* x,
                               double* jacobian) const;

  // 返回 4，表示 Manifold 空间（四元数）是 4 维的。即四元数本身的实际维数
  virtual int GlobalSize() const { return 4; }
  // 返回 3，表示切空间是 3 维的。即旋转矢量的实际维数
  virtual int LocalSize() const { return 3; }
};

2.1 QuaternionParameterization::Plus

/*
x:            待优化的四元数（x，在 Manifold，4维）
delta:        增量（delta，在 Tangent Space，3维）
x_plus_delta: 更新后的四元数，plus(x, delta)

plus(x, delta) = [cos(|delta|, sin(|delta|) / |delta| * delta] ⊗ x
参考http://ceres-solver.org/nnls_modeling.html#localparameterization
*/
bool QuaternionParameterization::Plus(const double* x,
                                      const double* delta,
                                      double* x_plus_delta) const {

/* --------1.将旋转矢量转换为四元数形式-------- */
  // 1.1 得到delta的模
  const double norm_delta =
      sqrt(delta[0] * delta[0] + delta[1] * delta[1] + delta[2] * delta[2]);
  if (norm_delta > 0.0) {
    // 1.2 得到sin(|delta|) / |delta|
    const double sin_delta_by_delta = (sin(norm_delta) / norm_delta);
    double q_delta[4];
    // 1.3 得到x_plus_delta
    q_delta[0] = cos(norm_delta);
    q_delta[1] = sin_delta_by_delta * delta[0];
    q_delta[2] = sin_delta_by_delta * delta[1];
    q_delta[3] = sin_delta_by_delta * delta[2];

/* --------2.采用四元数乘法更新-------- */
    // x_plus_delta = q_delta ⊗ x，注意这个乘法的顺序关乎求雅克比矩阵，具体说明参照ComputeJacobian
    QuaternionProduct(q_delta, x, x_plus_delta);
  } else {
    for (int i = 0; i < 4; ++i) {
      x_plus_delta[i] = x[i];
    }
  }
  return true;
}

2.2 QuaternionParameterization::ComputeJacobian

bool QuaternionParameterization::ComputeJacobian(const double* x,
                                                 double* jacobian) const {
  jacobian[0] = -x[1]; jacobian[1]  = -x[2]; jacobian[2]  = -x[3];  // NOLINT
  jacobian[3] =  x[0]; jacobian[4]  =  x[3]; jacobian[5]  = -x[2];  // NOLINT
  jacobian[6] = -x[3]; jacobian[7]  =  x[0]; jacobian[8]  =  x[1];  // NOLINT
  jacobian[9] =  x[2]; jacobian[10] = -x[1]; jacobian[11] =  x[0];  // NOLINT
  return true;
}

推导流程如下:

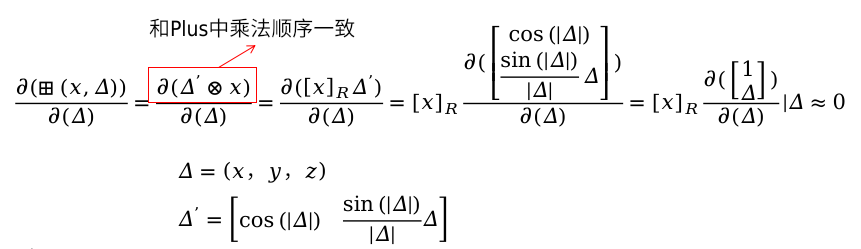
参照http://ceres-solver.org/nnls_modeling.html#localparameterization

根据

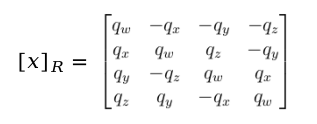
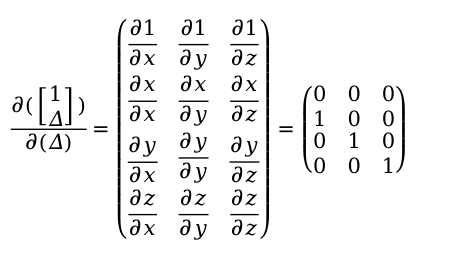
推导得到最后的雅克比矩阵为

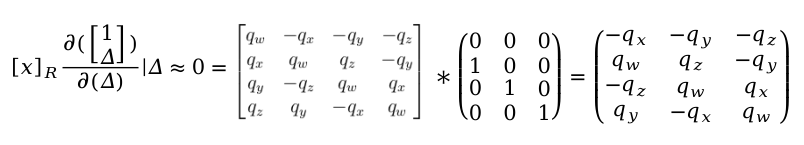
3.EigenQuaternionParameterization

// 和QuaternionParameterization类似。区别就是四元数在Eigen::Quaterniond中的内部内存分布为：x, y, z, w，不过构造顺序还是w，x，y，z
class CERES_EXPORT EigenQuaternionParameterization
    : public ceres::LocalParameterization {
 public:
  virtual ~EigenQuaternionParameterization() {}
  virtual bool Plus(const double* x,
                    const double* delta,
                    double* x_plus_delta) const;
  virtual bool ComputeJacobian(const double* x, double* jacobian) const;
  virtual int GlobalSize() const { return 4; }
  virtual int LocalSize() const { return 3; }
};

3.1 EigenQuaternionParameterization::Plus

bool EigenQuaternionParameterization::Plus(const double* x_ptr,
                                           const double* delta,
                                           double* x_plus_delta_ptr) const {
  Eigen::Map<Eigen::Quaterniond> x_plus_delta(x_plus_delta_ptr);
  Eigen::Map<const Eigen::Quaterniond> x(x_ptr);

  const double norm_delta =
      sqrt(delta[0] * delta[0] + delta[1] * delta[1] + delta[2] * delta[2]);
  if (norm_delta > 0.0) {
    const double sin_delta_by_delta = sin(norm_delta) / norm_delta;

    // Note, in the constructor w is first.
    Eigen::Quaterniond delta_q(cos(norm_delta),
                               sin_delta_by_delta * delta[0],
                               sin_delta_by_delta * delta[1],
                               sin_delta_by_delta * delta[2]);
    // 注意乘法的顺序
    x_plus_delta = delta_q * x;
  } else {
    x_plus_delta = x;
  }

  return true;
}

3.2 EigenQuaternionParameterization::ComputeJacobian

bool EigenQuaternionParameterization::ComputeJacobian(const double* x,
                                                      double* jacobian) const {
  jacobian[0] =  x[3]; jacobian[1]  =  x[2]; jacobian[2]  = -x[1];  // NOLINT
  jacobian[3] = -x[2]; jacobian[4]  =  x[3]; jacobian[5]  =  x[0];  // NOLINT
  jacobian[6] =  x[1]; jacobian[7]  = -x[0]; jacobian[8]  =  x[3];  // NOLINT
  jacobian[9] = -x[0]; jacobian[10] = -x[1]; jacobian[11] = -x[2];  // NOLINT
  return true;
}

推导流程如下:

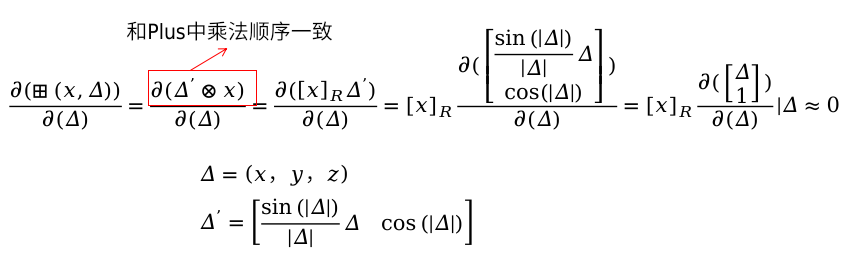
根据

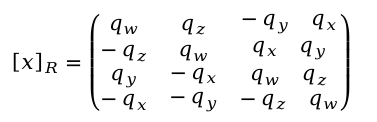
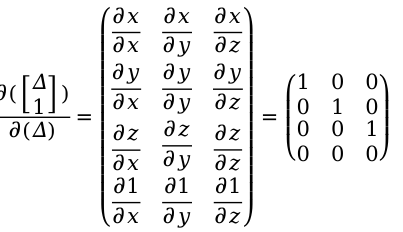
推导得到最后的雅克比矩阵为

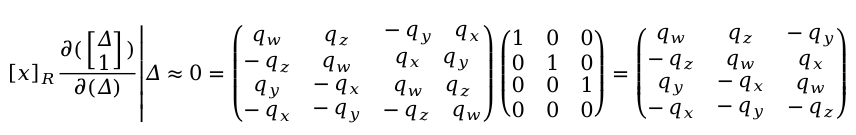
参考
https://www.cnblogs.com/JingeTU/p/11707557.html
https://cxybb.com/article/hltt3838/109693787
https://www.xiaotaoguo.com/p/ceres-usage-2/
https://blog.csdn.net/hjwang1/article/details/107869743