毫米波传感简介(一):调频连续波雷达—距离估计
本模块将介绍FMCW雷达运行的基础知识,讨论如何使用雷达进行距离估计并解答如下问题:
-
雷达如何估计它与该物体之间的距离?
![distance]()
-
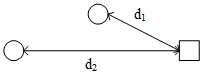
如果有多个物体,并且它们与雷达之间的距离是不同的,将会怎样?
![twodistance]()
-
两个物体能够相距多近而仍然能够被解析为两个物体?
![dres]()
-
什么决定雷达可以看到的最远距离?
![dmax]()
FMCW雷达的的核心是线性调频连续波(Chirp)。
1.什么是线性调频连续波(Chirp)?
线性调频脉冲是频率随时间以线性方式增长的正弦波。在该振幅-时间(\(\text{A-t}\))图中(如图1的上半部分),线性调频脉冲可能以频率为 \(f_{c}\) 的正弦波开始。然后,其频率逐渐增大,最后,假设以 \(f_{c}+ B\) 的频率结束,其中 \(B\) 是线性调频脉冲的带宽。因此,线性调频脉冲本质上是一种频率以线性方式进行调制的连续波。因此,我们使用术语调频连续波,或简称 FMCW。
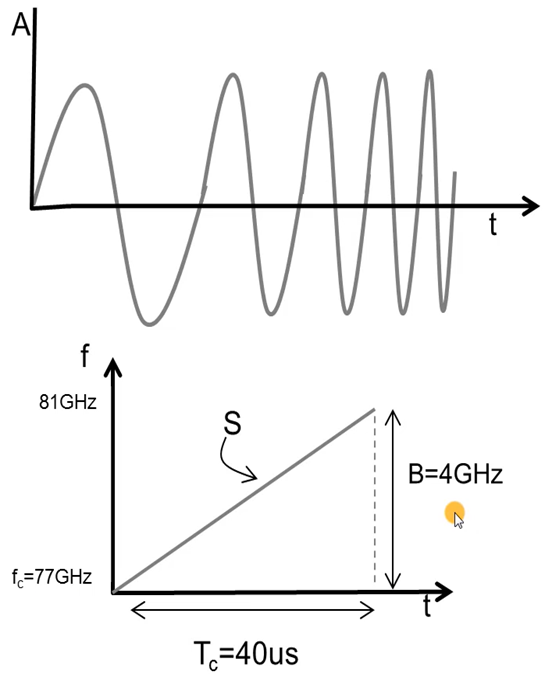
现在,如果在频率-时间图或者说 \(f-t\) 图中显示同一线性调频脉冲,它看起来会是什么样子的?
线性调频脉冲的频率随时间以线性方式增大,其中线性是关键词。因此,在 \(f-t\) 图中,线性调频脉冲会是一条具有特定斜率 \(S\) 的直线(如图1的下半部分)。
在图1中,线性调频脉冲跨越4GHz 的带宽,具有 40 微秒的\(T_{c}\) 时长,这对应于每微秒 100MHz 的斜率。后面将会看到,带宽\(B\) 和斜率 \(S\) 是用于定义系统性能的重要参数。
现在我们已经知道什么是线性调频脉冲,那么我们可以了解 FMCW雷达的工作原理了。
2. 1TX-1RX FMCW雷达
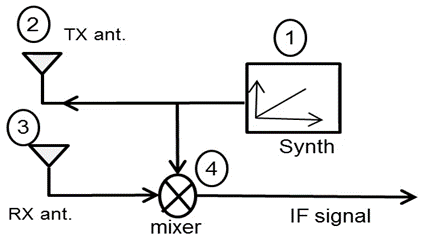
这是一个简化的FMCW 雷达框图,该雷达具有单个 TX天线和单个 RX 天线。该雷达的工作过程如下:
- 合成器生成一个线性调频脉冲。
- TX 天线将该线性调频脉冲发射出去, 当遇到物体时,该线性调频脉冲会反射回来。
- RX 天线接收反射的线性调频脉冲。
- RX 信号和 TX信号混频并生成 IF 信号 --IF 表示中频。
我们将在下一节中对 IF 信号进行更详细的分析。但是,首先让我们花点儿时间来了解这个称为混频器的组件。
2.1 混频器
下图是混频器的简单框图,其有两个输入端口一个输出端口。
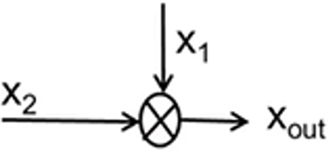
如果向混频器的两个输入端口输入两个正弦波,那么混频器的输出是具有以下两条性质的正弦波:
性质 1:输出的瞬时频率等于两个输入正弦波的瞬时频率的差值。因此,即使这些正弦波的频率随时间发生变化,任一时刻输出频率也将等于该时刻的输入频率差值。
性质 2:输出正弦波的起始相位等于两个输入正弦波的起始相位差值。
式(1)阐述了这两条性质,其中 \(x_{1}(t)\)和 \(x_{2}(t)\) 是两个输入,\(x_{out}(t)\) 是混频器的输出。
2.2 中频信号(IF signal)
下面我们加详细地看看雷达中混频器的工作原理。使用我们先前讨论过的 f-t 图可以对其进行最佳阐释,如下图所示:
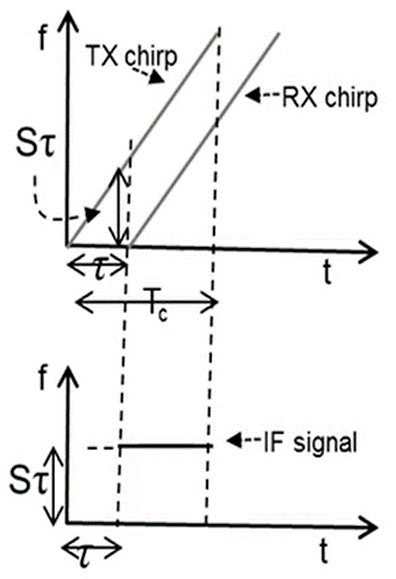
上图中 TX chirp 是发射器线性调频脉冲,RX chirp 是接收到的线性调频脉冲。请注意,接收到的线性调频脉冲是 TX 线性调频脉冲的延时副本。
现在,我假设雷达前方只有一个物体。因此,只有一个 RX 线性调频脉冲。回忆一下上一节混频器的内容,混频器的输出频率是其两个输入,即 TX 线性调频脉冲和 RX 线性调频脉冲的瞬时频率的差值。那么,为了生成 IF 信号的 \(f-t\) 图,我们需要将 TX chirp 的频率线减去 RX chirp 的频率线,而这两条线相互之间存在固定的距离。该固定的距离由线性调频脉冲的斜率乘以往返延迟给出:
因此,雷达前方的单个物体可生成一个包含单个频率的IF 信号,该频率由上式给出,即
\(\tau\)即从雷达到物体然后又返回的往返延迟,为
(3)式带入(2)式可得:
现在需要记住如下基本概念:雷达前方的单个物体可生成具有恒定频率的 IF 信号,该频率由 \(S2d/c\) 给出。
注意,IF 信号仅从在 RX 天线上接收到反射信号开始有效,这一点很重要。因此,如果您要使用ADC对该 IF 信号进行数字化,那么您需要确保仅在经过该时间 \(\tau\) 之后再接收样本,并且只能持续到TX 信号消失之前。
另外一点值得注意的是,往返延迟 \(\tau\) 通常是总线性调频脉冲时间的很小一部分。例如,对于最大距离为 300 米并且线性调频脉冲时间为 40 us 的雷达,该 \(\tau\) 与 \(T_{c}\) 的比率仅为 5%。
傅里叶变换的快速回顾
傅里叶变换是 FMCW 雷达信号处理的核心。我们将会看到,它用于距离、速度和角度估算。因此,我们将不时地稍微转移一下话题,回忆一下傅里叶变换的相关性质。
傅里叶变换将时域信号转换到频域中。时域中的单频信号会在频域中产生一个单峰。类似地,时域中的双频信号应在频域中产生两个峰值。但情况是否总是如此呢?看下面的示例:

在这个示例中,在观测窗口 T 内,红色正弦函数完成了两个周期,而蓝色正弦函数完成了 2.5 个周期。红色和蓝色之间的该 0.5 个周期差值似乎不足以解析频谱中的两个频率。在这里,只能看到与这两个正弦信号相关的单个频率峰值。

现在,让我们将观测窗口加倍,从 \(T\) 增加到 \(2T\),如图6所示。测窗口的加倍,导致红色正弦函数和蓝色正弦函数之间的差值为一个周期。现在在频谱中解析了这两个频率。所以,重点是,观测期越长,解析就越好。
一般而言,观测窗口 \(T\) 可以分隔以高于 \(1/T\) 赫兹进行分隔的频率分量。
3. 分辨雷达前的多个物体
到目前为止,我们已经讨论了雷达前方的单个物体。很容易将它扩展到雷达前方有多个物体的情况。假设有一个雷达,它正在发射单个线性调频脉冲,然后接收端获取了多个从不同物体反射的线性调频脉冲。每个脉冲具有不同量的延迟,具体取决于与物体之间的距离。因此,IF 信号将具有与其中每个反射相对应的频率,如下图所示:
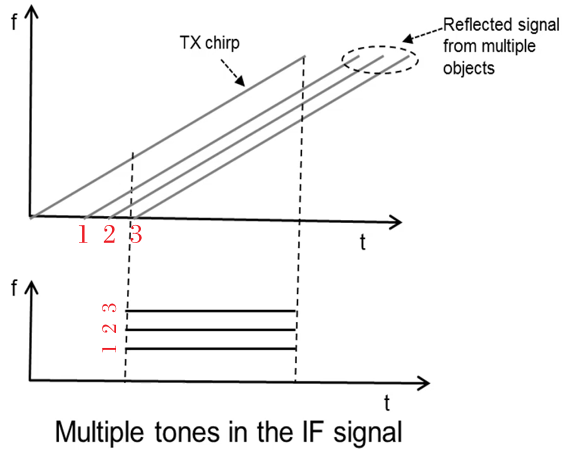
正如我们所了解到的,这些频率与距离成正比。因此,这1号线对应最小的频率并对应于最近的物体。而3号线对应于最远的物体。
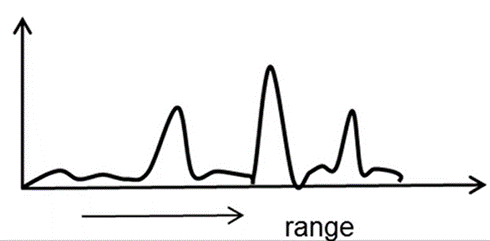
有关该 IF信号的傅里叶变换会显示多个峰值。这些峰值的频率将与对应物体的距离成正比,如下图所示:
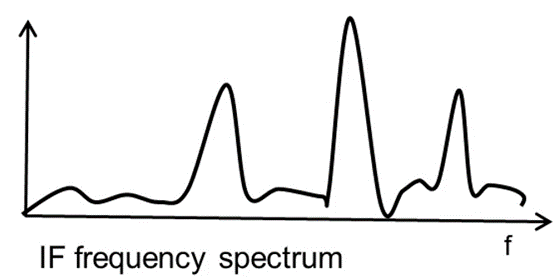
3.1 雷达距离分辨率
由于我们现在是在讨论多个物体,因此下一个问题自然是距离分辨率。也就是说,其中的两个物体能够相距多近而仍然能够在 IF频谱中解析为两个峰值?
下图的示例中,我们有两个从两个物体反射的线性调频脉。IF 信号的对应A-t 图显示了两个正弦波。但它们的频率太过接近,以至于它们在频谱中显示为单个峰值。

我们如何提高该雷达的距离分辨率?
可以从前面傅里叶变换的快速回顾中获得提示,通过增大 IF 信号的长度来扩展这两个正弦波的观测窗口。那么,线性调频脉冲得到扩展,从而扩展了 IF 信号的持续时间。这在频域中解析了两个峰值。
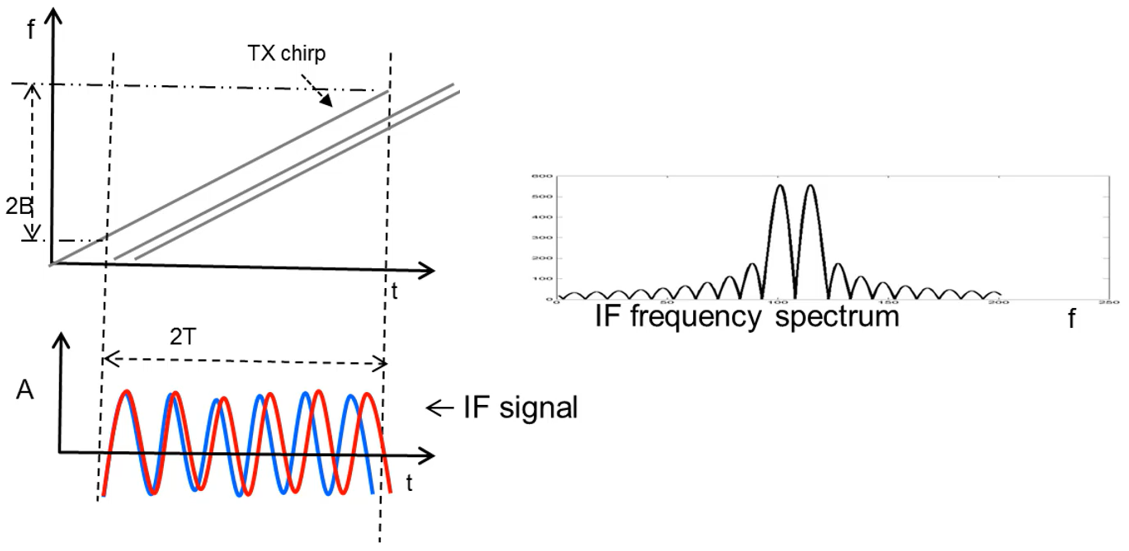
注意,增加 IF信号的持续时间成正比地增加了线性调频脉冲的带宽。这就提示我们,更大的带宽可能对应更好的距离分辨率。
现在,我们对如何提高雷达的距离分辨率有一些直观的认识,我们可以更进一步,实际推导该距离分辨率表达式。两个间距为 \(\Delta d\) 的物体,其 IF 频率间隔为:
为了使这两个频率在 IF 频谱中显示为不同的峰值,该频率间隔 \(\Delta f\) 必须大于$ 1 / {\text{The duration of IF signal}}$,如果我们忽略开始的一小部分,即往返延迟产生的 \(\tau\) 部分,那么这基本上等于线性调频脉冲的持续时间\(T_{c}\):
将(5)式带入(6)式,可以得到:
上式表示,只要两个物体之间的距离(间隔)大于\(\frac{c}{2B}\),就可以在 IF 频谱中分离它们。那么,这里的重点是,距离分辨率仅取决于线性调频脉冲覆盖的带宽:
小问题
下图有两个线性调频脉冲线性调频脉冲 A 和 B。A 的持续时间是 B 的两倍。但它们具有相同的带宽。这两个线性调频脉冲中的哪一个可以提供更好的距离分辨率?
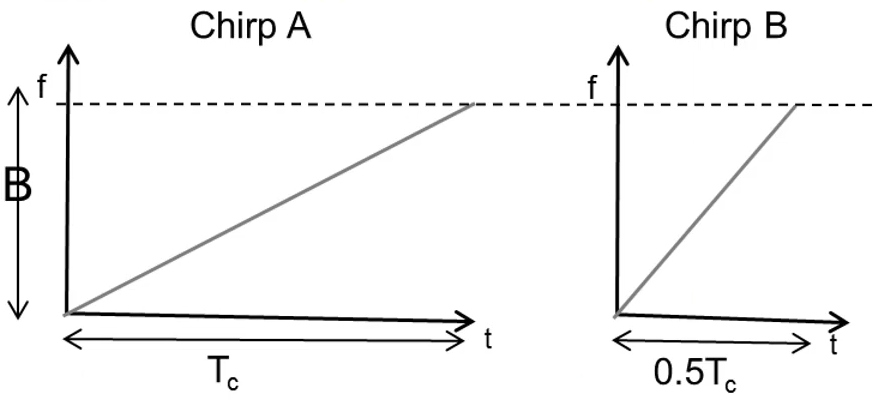
这两个线性调频脉冲具有相同的带宽 B。因此,根据(8)式,它们应具有相同的距离分辨率。但是,线性调频脉冲 A 具有更长的持续时间,因此具有更长的 IF 信号观测窗口。因此,凭直觉,如果您考虑傅里叶变换的性质,线性调频脉冲 A 的分辨率应好于线性调频脉冲 B。我们如何解决该矛盾?
4. 数字化IF信号
在大多数雷达中会对 IF 信号进行数字化,以供后续处理。那么,它首先会进行低通滤波,然后由 ADC 进行数字化,接着被发送到合适的处理器,如 DSP。DSP 可能首先执行傅里叶变换,以估算物体的距离,随后执行其他种类的处理,以估算这些物体的速度和到达角,如下图所示:
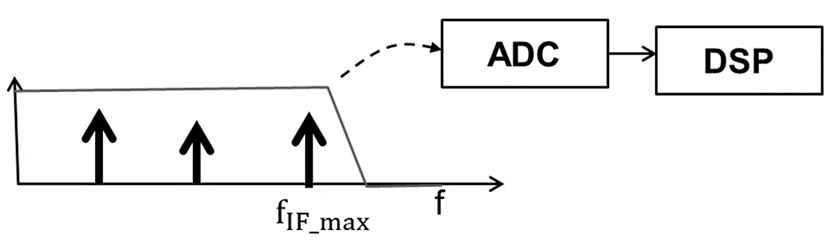
每当我们要对信号进行数字化时,我们就需要知道目标带宽,以便可以适当地设置低通滤波器和 ADC 采样率。那么,假设我们对零到最大距离\(d_{\max}\) 之间的物体感兴趣。IF 信号的最大频率将为:
相应地,目标带宽将从零到该最大 IF 频率,这意味着低通滤波器的截止频率应高于该\(f_{IF_{max}}\)。
此外,ADC 应具有高于该值的采样率:
因此,可以看到,ADC 的最大采样率可能会限制雷达可以看到的最大距离。
如果 ADC采样率和 IF带宽是传感器的瓶颈,那么可以对斜率和最大距离进行折衷。通常,雷达倾向于针对较大的\(d_{\max}\) 使用较小的斜率。
重新回到前面的小问题:

5. 测距过程总结
下图总结了到目前为止我们已经讨论的所有内容:
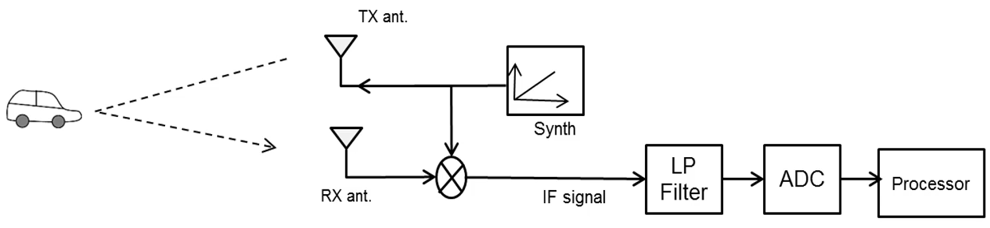
这是具有单个发射天线和单个接收天线的FMCW 雷达的框图。让我们来查看估算物体的距离所涉及的一系列事件:
- 首先,合成器生成一个线性调频脉冲;
- 该线性调频脉冲通过 TX 天线进行发射;
- 雷达前方的多个物体后反射线性调频脉冲;
- 接收器收到该线性调频脉冲的延迟版本;
- 接收到的信号和发射的信号进行混频,从而产生 IF 信号, 该 IF 信号包含多个频率,其中每个频率与对应物体的距离成正比;
- IF 信号进行低通滤波并数字化,注意,ADC 的采样率必须与最大探测距离匹配。
- 对数字化数据进行处理,即,执行 FFT。
- 频谱中峰值的位置直接对应于物体的距离。
请注意,在这里,我绘制FFT 时 x 轴上显示的是距离,而不是 IF频率。
5.1 关键概念/方程
- 距离为 d 的物体会生成 IF频率为:
- 距离分辨率仅取决于线性调频脉冲跨越的带宽:
- ADC 采样率 Fs 限制雷达可以探测的最大距离:
5.2 射频带宽 vs. IF带宽
带宽和 FMCW雷达时,通常有两种重要的带宽。射频带宽和 IF 带宽。应清晰地区分这两者,这一点很重要。
射频带宽:线性调频脉冲跨越的带宽。
较大的射频带宽可直接转换为较好的距离分辨率。射频带宽的范围通常为几百 MHz至几 GHz。例如,4GHz 的射频带宽可转换为 4 厘米的距离分辨率。400MHz 的射频带宽可转换为大约 30 厘米的距离分辨率。
IF 带宽: 较大的 IF 带宽主要可以使雷达看到较大的最大距离。还可以实现较快的线性调频脉冲。我说较快的线性调频脉冲,是指具有较高斜率的线性调频脉冲。
典型雷达的IF 带宽处于低 MHz 范围内。这是有关FMCW 雷达的要点之一,您可以具有跨越较大带宽的射频信号,比如 4GHz,但您的 ADC仅需要对几 MHz 的信号进行采样。
6. 后记
- 有两个与雷达的距离相同的物体。距离 FFT 看起来会是什么样的?
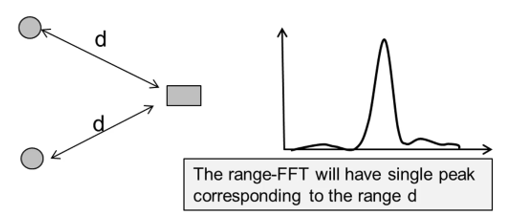
现在,由于这些物体的距离是相同的,因此距离 FFT 将具有与该距离 d 相对应并受到这两个物体影响的单个峰值。那么,我们如何分离这两个物体呢?
事实证明,如果这两个物体相对于雷达具有不同的速度,那么可以通过进一步的信号处理分离它们。要理解这一点,我们需要实际看看 IF 信号的相位。

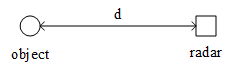
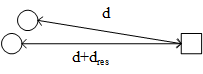
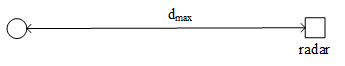

 浙公网安备 33010602011771号
浙公网安备 33010602011771号