QAM信号的最佳检测和错误概率

在QAM信号的最佳检测中，需要两个滤波器匹配于

\[\phi_{1}(t)=\sqrt{\frac{2}{\mathcal{E}_{g}}}g(t)\cos2\pi f_{c}t,\quad \phi_{2}(t)=-\sqrt{\frac{2}{\mathcal{E}_{g}}}g(t)\sin2\pi f_{c}t\tag{1} \]

匹配滤波器的输出\(\bold{r}=(r_{1},r_{2})\)用来计算相关度量\(C(\bold{r,s_{m}})=2\bold{r\cdot s_{m}}-\mathcal{E}_{m}\)，且选择其中的最大值。判决域取决于星座的形状，一般错误概率没有闭式(Closed Form)。

为了求QAM信号的差错概率，必须详细说明信号的星座图。首先看\(M=4\)个点的QAM信号集。下图所示为两种4个点的QAM信号星座图：第一种是一个四相调制信号，第二种是具有2个幅度电平和四个相位的QAM信号。

图1：两种4点QAM信号星座图

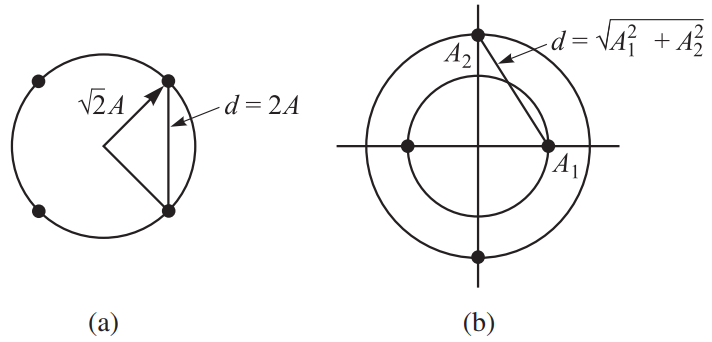
因为错误概率主要取决于信号点之间的最小距离，对这两种信号星座图施加条件\(d_{\min}=2A\)，并根据所有信号点是等概的前提条件来计算平均发送功率。

对四相信号，有

\[\mathcal{E}_{\text{avg}}=2A^{2} \]

对于2个幅度电平、4个相位的QAM信号，将信号点置于半径为\(A\)和\(\sqrt{3}A\)的圆周上，因此\(d_{\min}=2A\)，且

\[\mathcal{E}_{\text{avg}}=\frac{1}{4}[2(3A^{2})+2A^{2}]=2A^{2} \]

这与四相信号具有相同的平均功率，因此，这两个信号集的差错概率性能是相同的。

接下来研究\(M=8\)的QAM信号。此时，有许多可能的信号星座图。我们研究图2所示的四个信号星座图，该图中的所有星座都由两个幅度组成且信号点之间的最小距离均为2A。图中每个信号点的坐标\((A_{mc},A_{ms})\)已由A归一化。假设信号点是等概的，平均发送信号能量是

\[\mathcal{E}_{\text{avg}}=\frac{1}{M}\sum_{m=1}^{M}(A_{mc}^{2}+A_{ms}^{2})=\frac{A^{2}}{M}\sum_{m=1}^{M}(a_{mc}^{2}+a_{ms}^{2}) \]

式中，\((a_{mc},a_{ms})\)是由A归一化的信号点坐标。

图2：4种8点QAM信号星座图

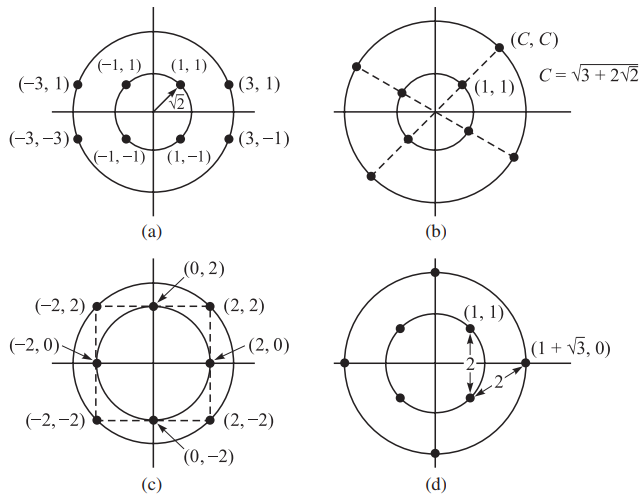
图2中的两个信号集(a)和(c)中的信号点落在一个矩形的格栅上且\(\mathcal{E}_{\text{avg}}=6A^{2}\)。信号集(b)要求平均发送能量\(\mathcal{E}_{\text{avg}}=6.83A^{2}\)，而(d)要求\(\mathcal{E}_{\text{avg}}=4.73A^{2}\)。因此为达到相同的错误概率，(d)要求的功率比(a)和(b)大约小1dB，而比(c)小1.6dB。(d)被称为最佳8-QAM信号星座图，因为它对给定信号点之间最小距离所要求的功率最小。

对于\(M\ge 16\)，在二维空间中选择QAM信号点的可能性更大。例如，可对M=16选择原型多幅度星座图，如图3所示。

图3：16-QAM星座图示例

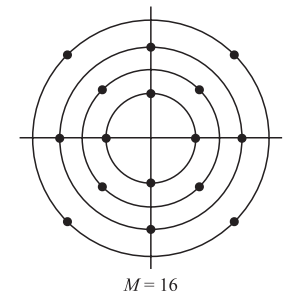
在这种情况下，给定幅度电平上的信号点与邻近幅度电平上信号点相位旋转\(\pi/4\)。16-QAM信号星座图是最佳8-QAM信号星座图的推广。然而，对AWGN信道，圆周形的16-QAM信号星座图不是最佳16-QAM信号星座图。

矩形QAM信号星座图具有容易产生的独特优点，即通过在两个正交载波上施加两个PAM信号来产生；此外，他们也容易解调。虽然对于\(M\ge 16\)来说，该星座图并不是最佳M-QAM信号星座图，但是对于要达到给定最小距离的要求来说，该星座图所需要的平均发送功率仅稍大于最佳M-QAM信号星座图所需要的平均功率。由于这些原因，矩形M-QAM信号在实际中应用得最多。

在\(k\)为偶数，方形星座图的特殊情况下，可以导出差错概率的精确表达式，此时星座的做小距离为

\[d_{\min}=\sqrt{\frac{6\log_{2}M}{M-1}\mathcal{E}_{\text{bavg}}} \]

方形星座可看作两个在同相(In-Phase)和正交(quadrature)方向上的\(\sqrt{M}-PAM\)星座图。如果在两个PAM信号之一中\(n_{1}\)或\(n_{2}\)足够大，则差错发生。因此，该QAM星座图的正确检测概率是构成PAM系统正确检测概率的乘积，即

\[P_{c,M-QAM}=P_{c,\sqrt{M}-PAM}^{2}=(1-P_{e,\sqrt{M}-PAM})^{2} \]

那么差错概率为

\[P_{e,M-QAM}=1-(1-P_{e,\sqrt{M}-PAM})^{2}=2P_{e,\sqrt{M}-PAM}\left(1-\frac{1}{2}P_{e,\sqrt{M}-PAM}\right)\tag{2} \]

结合PAM信号差错概率的表达式，可得

\[\begin{aligned} P_{e,\sqrt{M}-PAM}&=2\left(1-\frac{1}{\sqrt{M}}\right)Q\left(\frac{d_{\min}}{\sqrt{2N_{0}}}\right)\\ &=2\left(1-\frac{1}{\sqrt{M}}\right)Q\left(\sqrt{\frac{3\log_{2}M}{M-1}\frac{\mathcal{E}_{\text{bavg}}}{N_{0}}}\right) \end{aligned}\tag{3}\]

将(3)式带入(2)式，可得

\[\begin{aligned} P_{e,M-QAM}&=4\left(1-\frac{1}{\sqrt{M}}\right)Q\left(\sqrt{\frac{3\log_{2}M}{M-1}\frac{\mathcal{E}_{\text{bavg}}}{N_{0}}}\right)\times \\ &\quad \left[1-\left(1-\frac{1}{\sqrt{M}}\right)Q\left(\sqrt{\frac{3\log_{2}M}{M-1}\frac{\mathcal{E}_{\text{bavg}}}{N_{0}}}\right)\right]\\ &\le 4Q\left(\sqrt{\frac{3\log_{2}M}{M-1}\frac{\mathcal{E}_{\text{bavg}}}{N_{0}}}\right) \end{aligned} \tag{4} \]

对于大M值和适当高的比特SNR，式(4)确定的上边界是相当紧密的。下图画出了M-QAM的符号差错概率的曲线，它是比特SNR的函数。虽然式(4)是由方形星座图求得的，但它是具有\(M=2^{k}\)个点的一般QAM星座图在大M时的良好近似，该一般QAM星座图形状是方形的或十字形的。

图4：QAM符号差错概率

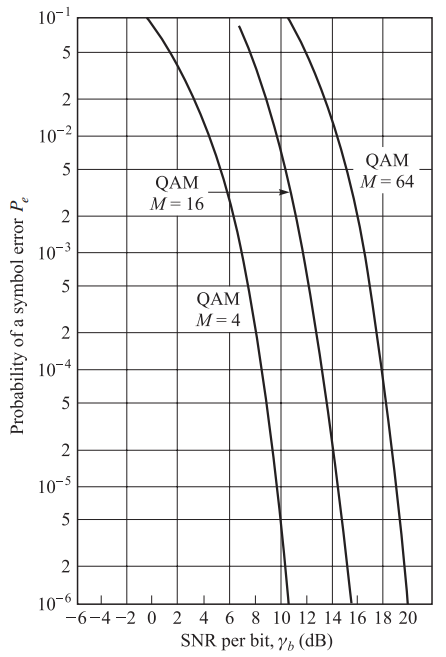
对比M-QAM，ASK和MPSK的性能，可以看出，不像PAM和PSK信号传输方式增加速率的代价是6dB/bit，QAM的代价是3dB/bit。这表明QAM的功率效率比PAM和PSK高，但PSK的优点是其恒包络特性。