数控振荡器原理及实现-原理

1. 什么是NCO

数控振荡器NCO(Numerical Controlled Oscillator)是一种从 相位 出发直接合成所需要波形的数字频率合成技术。可以通过设置不同的频率控制字实现输出不同频率的正余弦信号的功能。FPGA实现NCO功能可以分为相位累加器和查找表两部分，如下图所示：

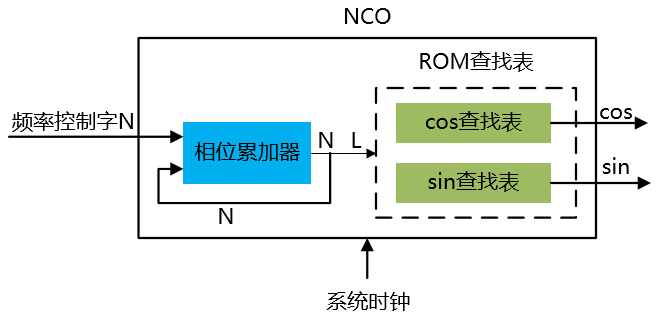
2. NCO原理分析

相同时间间隔，相位变化的快慢能够反映出频率的大小：

\[\omega = \frac{d\phi}{dt}\tag{1} \]

以相位累加器溢出一次对应正余弦函数旋转一周，那么每个周期对应的相位偏移量为

\[\Delta \phi_{r} = \frac{2\pi}{2^{N}}\tag{2} \]

添加一个控制字，FCW(Frequency Control Word)来线性调整每个周期的相位偏移的大小，进而可以得到不同的频率

\[\Delta \phi = \text{FCW}\cdot\Delta\phi_{r}=\text{FCW}\frac{2\pi}{2^{N}}\tag{3} \]

相位变化\(\Delta\phi\)所使用的时间为一个周期，即\(\Delta t = \frac{1}{f_{sys}}\)。于是对应的角频率为

\[\omega = \frac{\Delta\phi}{\Delta t}=\frac{\text{FCW}\cdot2\pi\cdot f_{sys}}{2^{N}}\tag{4} \]

至此可以得到输出正/余弦波性的的频率与系统工作频率之间的关系为：

\[f=\frac{\omega}{2\pi}=\frac{FCW\cdot f_{sys}}{2^{N}}\tag{5} \]

由上式可知可以通过调整FCW来改变输出信号的频率。

3. 相位累加器

根据相应的FCW输出不同的相位值，其中FCW作为相位递增的步进值。
例如：N=2, 当FCW=1时，相位累加器输出分别为(初相为0):

\[2'd0\rightarrow\frac{0*2\pi}{4};2'd1\rightarrow\frac{1*2\pi}{4};2'd2\rightarrow\frac{2*2\pi}{4};2'd3\rightarrow\frac{3*2\pi}{4} \]

四个点为一个周期。周期的计算方式为：$$2\pi/\Delta\theta = \frac{2^{N}}{\text{FCW}}$$

当N=2，FCW=2时，相位累加器输出分别为(初相位0)：

\[2'd0\rightarrow\frac{0*2\pi}{2^{2}}\times 2;\quad 2'd1\rightarrow\frac{1*2\pi}{2^{2}}\times 2 \]

相位累加器输出作为读取查找表的ROM地址

4. ROM查找表

相位累加器的位宽N决定了NCO的频率分辨率，决定了相位累加输出相位值，同时也决定了读取ROM查找表的地址。

例如：N=2时，一个完整周期的相位累加器输出分别为（初相为0）：

\[2'd0\rightarrow\frac{0*2\pi}{4};2'd1\rightarrow\frac{1*2\pi}{4};2'd2\rightarrow\frac{2*2\pi}{4};2'd3\rightarrow\frac{3*2\pi}{4} \]

FCW不同只是从完整的相位累加值选取部分值作为相位累加器的输出；此时完整正余弦查找表的深度应该设置为\(2^2=4\)，至于数据的位宽根据实际正余弦数据需求精度进行设置。

例如：N=32，完整正余弦查找表的深度应该设置为\(2^{32}\)，这样的话查找表将会很庞大，很浪费资源。实际使用中ROM中只存储\(2^{8}=256\)个正余弦值，此时在处理时就需要将相位累加器输出的相位值（即ROM查找表的理论32位宽的地址）进行截位，截位后的相位累加器输出相位值位宽为8bits，作为查找表的实际地址。

可以利用正余弦波形的周期特性和对称特性可以只在ROM中存储1/4周期的正余弦值，这样也大大减少资源的使用。