加法器的硬件实现
1. 加法运算
加法运算可以说是数字信号处理中最基本的运算,减法、乘法运算都可以通过加法运算实现。加法运算也可以说是数字信号处理中最简单的运算。目前的FPGA中,可采用分布式逻辑资源实现加法,也可采用嵌入式资源实现加法。
1.1 一位全加器
一位加法器是实现多位加法器的基础。它的输入端是被加数A、加数B以及较低位的进位\(C_{in}\);输出端是本位和\(S\)以及向较高位的进位\(C_{out}\)。根据二进制加法运算规则可知其真值表如表1.1所示。由真值表利用卡诺图化简可得输出与输入的逻辑关系式,如式\((1),(2)\)所示。
| A | B | \(C_{in}\) | S | \(C_{out}\) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
表1.1 一位全加器真值表
式中\(\oplus\)表示异或(XOR)。
根据逻辑关系表达式,可进一步得出一位全加器的硬件电路图,如图1.1所示。加法运算的三个要素是被加数、加数和低位的进位,它们共同决定了输出和与高位的进位。
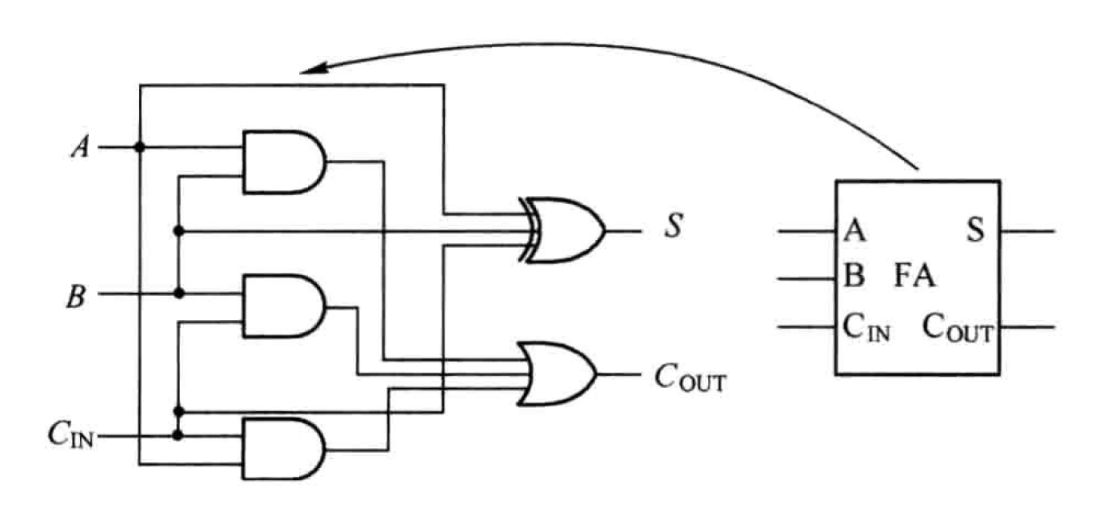
图1.1 一位全加器的硬件电路图
1.2 二进制加法原理
加法运算最有可能出现的问题就是溢出,即运算结果超出了给定位宽所能表示的数的范围。例如,两个一位十进制数相加\(9+8\),其结果为17,显然是无法用一位十进制数表示的。
在硬件设计时,为了防止溢出而导致计算结果错误,就要预先采取一定的措施。这里以两个4bits二进制数相加为例。它们均以二进制补码表示。4bits二进制补码所能表示的数的范围是\([-2^{4-1},2^{4-1}-1]\)即[-8,7]。分以下三种情况进行分析:
(1)正数 + 正数; (2)正数 + 负数;(3)负数 + 负数。
1. 正数 + 正数
两个4bits二进制数相加,其结果可能是4bits二进制数(未溢出),也可能是5bits二进制数(溢出)。当结果为前者时较好理解,如1+3=4,二进制计算如图1.2所示。图1.2(b)是对被加数与加数进行符号位扩展之后相加。这也进一步明确符号位扩展是不影响数值大小的。当结果为后者时,如3+6=9,二进制计算如图1.3所示。图1.3(b)是对被加数与加数进行符号位扩展之后相加。
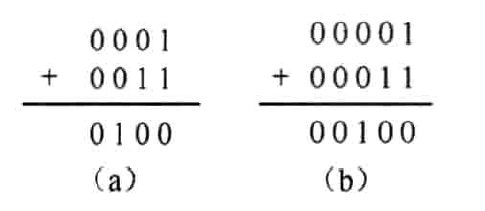 图1.2 两个4位二进制正数相加未溢出情形 |
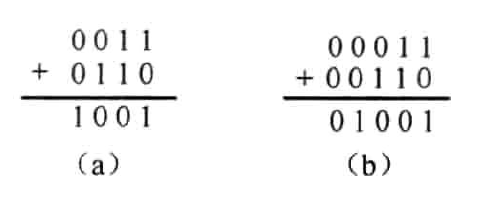 图1.3 两个4位二进制正数相加溢出情形 |
对于图1.3(a),如果为无符号数结果是正确的,如果是有符号数,那么(1001)是-7的补码,显然结果是错误的。错误的原因在于数值9已经超出了4bits二进制数所能表示的数的范围,即溢出。而结果又始终是以补码形式看待的。这正是执行加法运算时非常关键的一个问题。对于图1.3(b),无论是从有符号数还是无符号数的角度看,结果都是正确的。
2. 正数 + 负数
正数 + 负数也就是减法,减法实质上仍是加法,因为减去一个数等效于加上这个数的补码。显然,这种情况下不会溢出。以2+(-3)为例,二进制计算如图1.4所示。其中(-3)的4bits二进制补码为(1101),5bits二进制补码为(11101)。计算结果(1111)是(-1)的4bits二进制补码,(11111)是(-1)的5bits补码。可见结果是正确的。

3. 负数 + 负数
分溢出与未溢出两种情况。对于未溢出,以(-2)+(-3)为例说明,二进制补码计算如图1.5所示。
对于结果(11011),其低4bits(1011)是(-5)的4bits二进制补码,(11011)是(-5)的5bits二进制补码,(111011)是(-5)的6bits二进制补码,显然结果是正确的。
对于溢出,以(-3)+(-6)为例说明,二进制补码计算如图1.6所示。对于图1.6(a),如果只取低4bits(0111),显然结果是错误的。对于图1.6(b)取低5bits结果是正确的,前提是对两个数进行了符号位扩展。符号位扩展并不改变数值大小。
 图1.5 两个4位二进制负数相加未溢出情形 |
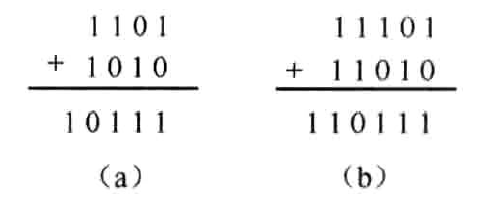 图1.6 两个4位二进制负数相加溢出情形 |
对于其他情况,正数减去负数可归结为正数加正数,负数减负数可归结为正数加负数。通过以上分析,可得出如下结论:两个N位二进制补码相加,为防止溢出时导致计算结果错误,可将这两个数先进行符号位扩展,变成N+1位二进制数,然后相加,结果亦取N+1位,可保证运算正确。
根据多位加法器原理可知,对于两个Nbits二进制补码数相加,可利用N个一位全加器搭建而成。如图1.7所示即为两个4bits二进制补码数相加A+B的硬件电路图。其中被加数、加数、和的最高位分别为\(A_{3},B_{3},S_{4}\)。末尾级进位端最终形成了和的符号位。
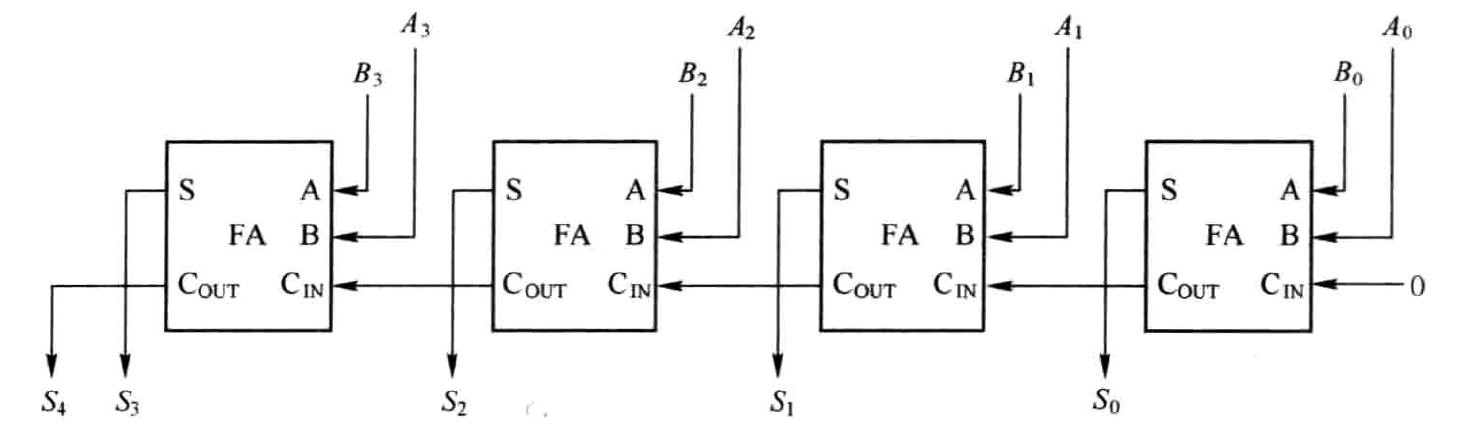
由于减去一个数等效于与这个数的补码相加,这样减法操作就变成了加法操作。根据“取反加一”的求补码方法,对图1.7稍作改动即可形成图1.8所示的4bits二进制数相减A-B的硬件电路图。图中首先对减数通过反相器逐位取反,并将最低的进位端设置为1。
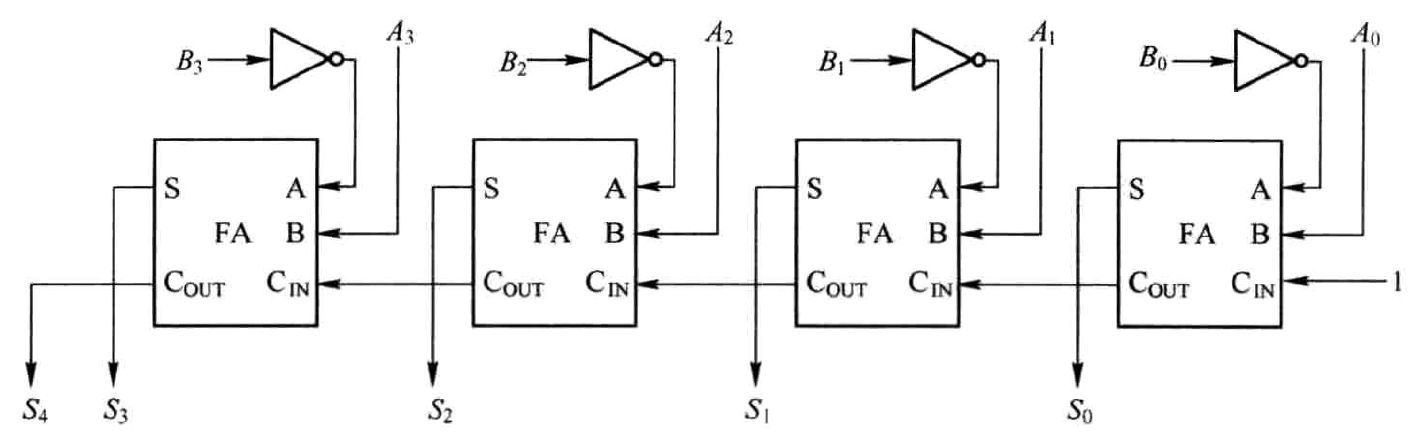
对比图1.7和图1.8可以发现,两者的结构是相同的,很多逻辑资源是可以共享的。为此,将两者合二为一,引入控制端control,通过它来切换加法操作与减法操作。这样形成了图1.9所示的硬件电路图。图中,当control为0,执行A+B,当control为1时,执行A-B。
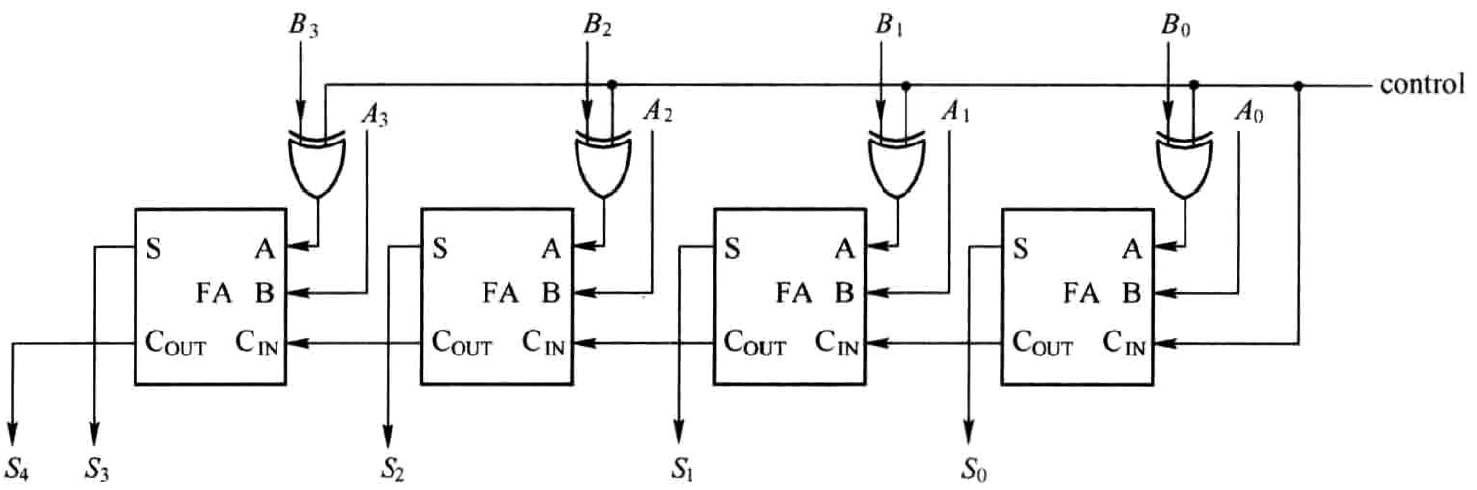
采用HDL描述多位加法器或多位减法器时,并不需要先构建一个全加器,再按照上述电路图搭建(上述电路图只是为了阐述其实现原理),而是符号位扩展之后直接用"+"或"-"即可。通常情况下,用Vivado综合,加法器会用查找表、进位链等资源实现,但可通过设置综合属性USE_DSP48使得加法器用DSP48实现。
对于可切换的加法、减法电路,可采用图1.10所示方式搭建,利用HDL描述非常方便。图中D表示D触发器,本书后续章节中均采用此方式表示D触发器。

1.3 复数加法
在某些应用场合需要执行复数加法运算。复数加法的原理很简单,实部和实部相加得到和的实部,虚部和虚部相加得到和的虚部,如式(1.3)所示。式中,a,b,c,d,e,f均为实数,j为虚数单位。可见,复数加法最终被分解为实数加法。一次复数加法由两次实数加法构成。
根据上述原理可得如图1.11所示的硬件电路结构。
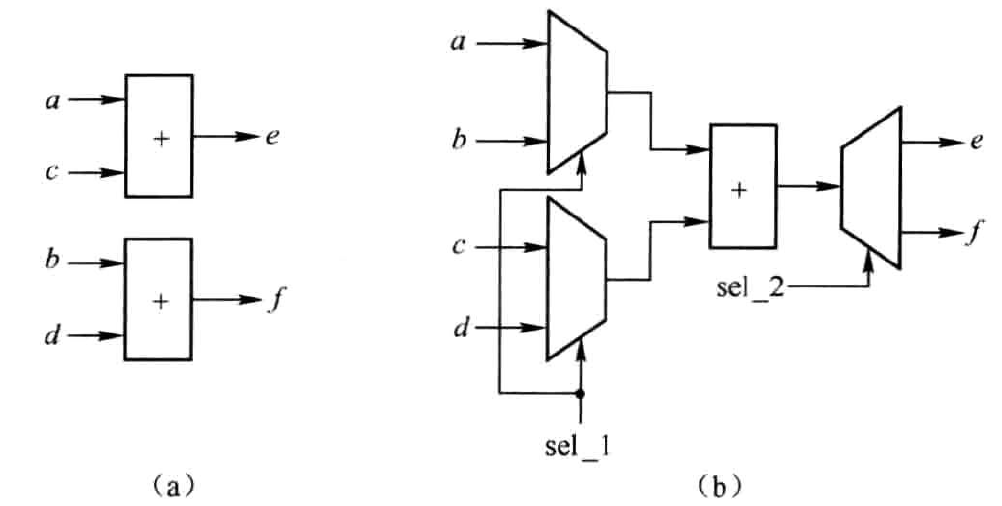
图1.11(a)采用了两个加法器,并执行实部和虚部的加法。图1.11(b)则采用了一个加法器,通过分时复用,分别求和。显然,前者在速度上有优势,后者在资源上有优势。
1.4 加法树与加法链
在很多应用场合都会涉及多个数相加求和,如式(4)所示
此时,可采用加法树,也可采用加法链。加法树结构如图1.12所示。为了提高系统速度,采用了流水线技术。
图1.12中是一个三级加法树,每级加法器的位宽依次递增,防止溢出导致计算错误。全流水,从输入到输出需要3个时钟周期。显然,将此结构推广,如果要求N个数的和,则需要\(\text{ceil}(\text{log}_{2}(N))\)级加法树。该结构非常清晰,可高速运行。但整个设计性能的瓶颈在于末级的加法树,如图1.12的阴影所示,它们将消耗较大的功耗。
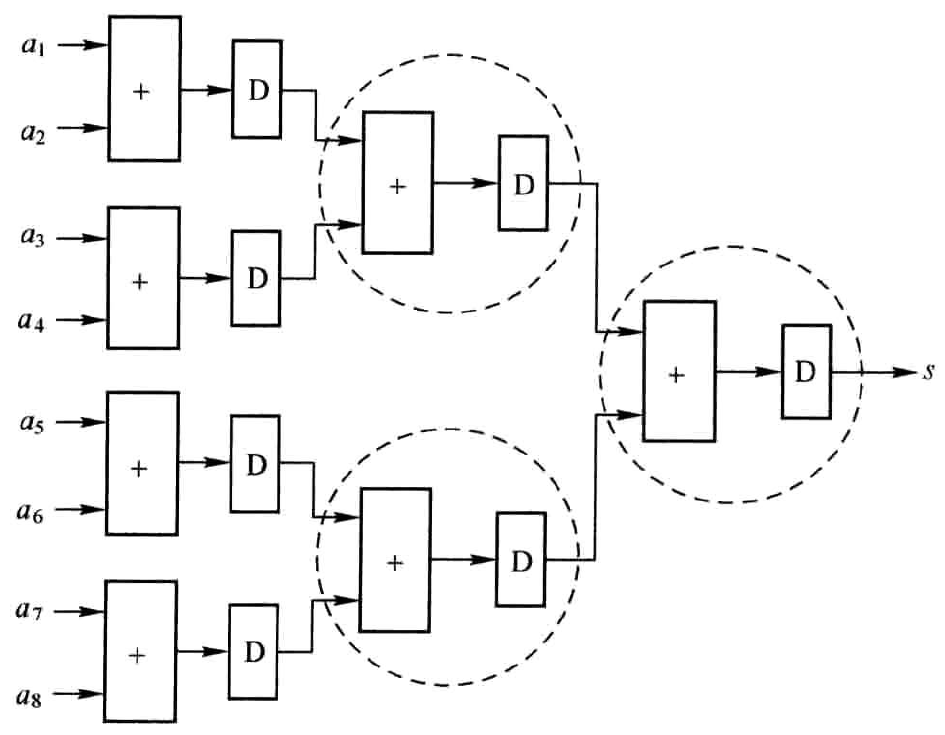
对于式(4)若采用加法链结构,如图1.13所示。为了正确相加,\(a_{3}\)相比\(a_{2}\)和\(a_{1}\)推迟一个时钟周期进入加法器,\(a_{4}\)相比于\(a_{3}\)推迟一个时钟进入加法器,后续各加数进入时刻以此类推。从而,从输入到输出需要7个时钟周期(Latency=7)。显然,相对于加法树,此结构时许稍显复杂,但结构中每个加法器的“等级”是一致的。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号