【剑指 Offer 55 - I. 二叉树的深度 简单】【104. 二叉树的最大深度 简单】【剑指 Offer 55 - II. 平衡二叉树 简单】【LeetCode110. 平衡二叉树 简单】

1.【剑指 Offer 55 - I. 二叉树的深度 简单】【104. 二叉树的最大深度 简单】

（1）题目描述

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

例如：

给定二叉树 [3,9,20,null,null,15,7]，

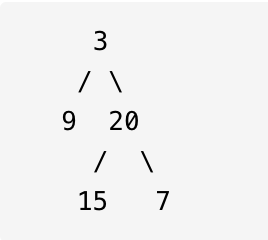
返回它的最大深度 3 。

（2）思路

利用递归，分别求左右子树的深度，树的深度等于左右子树深度的最大值 + 1。

（3）代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == NULL)
            return 0;
        int leftDepth = maxDepth(root->left);
        int rightDepth = maxDepth(root->right);
        return max(leftDepth, rightDepth) + 1;
    }
};

 

【剑指 Offer 55 - II. 平衡二叉树 简单】【LeetCode110. 平衡二叉树 简单】

1. 题目描述

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

2. 思路

如果采用中序遍历，求左右子树深度的过程中，会有大量的重复遍历。因此采用后序遍历，因为在遍历根节点时，左右子树都已遍历完毕，因此不存在重复的遍历。只需再遍历左右子树的过程中记录好左右子树的深度就行了。

3. 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool judgeBalance(TreeNode* root, int& depth) {
        if(root == NULL) {
            depth = 0;
            return true;
        }
        int left = 0, right = 0;
        if(judgeBalance(root->left, left) && judgeBalance(root->right, right)) {
            if(abs(left - right) <= 1) {
                depth = 1 + max(left, right);
                return true;
            }
        }
        return false;
    }
    bool isBalanced(TreeNode* root) {
        if(root == NULL)
            return true;
        int depth = 0;
        return judgeBalance(root, depth);
    }
};