题目地址

This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.

请输入图片描述

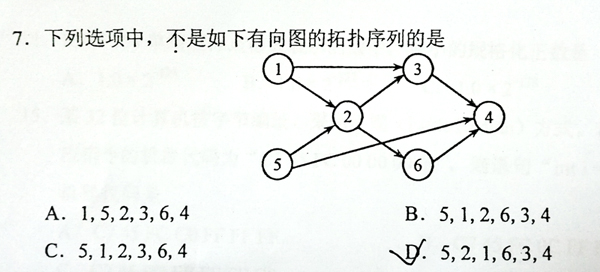
Input Specification:
Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 1,000), the number of vertices in the graph, and M (≤ 10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.

Output Specification:
Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.

Sample Input:
6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6

Sample Output:
3 4

#include <cstdio>
#include <cstring>
#include<iostream>
#include <vector>
#include<math.h>
#include<string>            //看吧，没必要用G的；
#include<queue>
#include <algorithm>            
#include<set>
#include<map>
using namespace std;
const int maxn=100010,inf=1000000000;
int n,m,k;map<int,int> in_degree,temp;vector<int>v[maxn],ans;
int main(){
    cin>>n>>m;int v1,v2;
    for(int i=0;i<m;i++){
        cin>>v1>>v2;
        v[v1].push_back(v2);in_degree[v2]++;
    }
    cin>>k;
    for(int q=0;q<k;q++){
        temp=in_degree;
        int flag=1;
        for(int i=1;i<=n;i++){
            cin>>v1;
            if(temp[v1]>0) flag=0;
            for(int j=0;j<v[v1].size();j++) temp[v[v1][j]]--;
        }
        if(!flag) ans.push_back(q);
    }
    for(int i=0;i<ans.size();i++){
        if(i!=0) cout<<" ";
        cout<<ans[i];
    }
}