1053 Path of Equal Weight (30分)
Given a non-empty tree with root R, and with weight W
i
assigned to each tree node T
i
. The weight of a path from R to L is defined to be the sum of the weights of all the nodes along the path from R to any leaf node L.
Now given any weighted tree, you are supposed to find all the paths with their weights equal to a given number. For example, let's consider the tree showed in the following figure: for each node, the upper number is the node ID which is a two-digit number, and the lower number is the weight of that node. Suppose that the given number is 24, then there exists 4 different paths which have the same given weight: {10 5 2 7}, {10 4 10}, {10 3 3 6 2} and {10 3 3 6 2}, which correspond to the red edges in the figure.
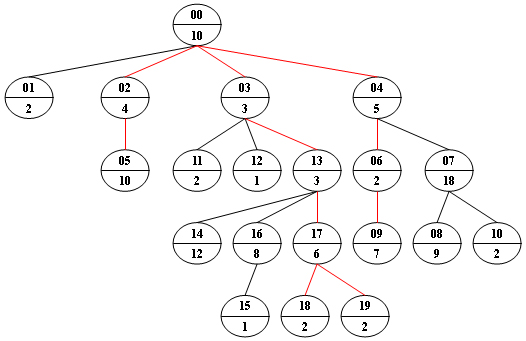
Input Specification:
Each input file contains one test case. Each case starts with a line containing 0<N≤100, the number of nodes in a tree, M (<N), the number of non-leaf nodes, and 0<S<2
30
, the given weight number. The next line contains N positive numbers where W
i
(<1000) corresponds to the tree node T
i
. Then M lines follow, each in the format:
ID K ID[1] ID[2] ... ID[K]
where ID is a two-digit number representing a given non-leaf node, K is the number of its children, followed by a sequence of two-digit ID's of its children. For the sake of simplicity, let us fix the root ID to be 00.
Output Specification:
For each test case, print all the paths with weight S in non-increasing order. Each path occupies a line with printed weights from the root to the leaf in order. All the numbers must be separated by a space with no extra space at the end of the line.
Note: sequence {A
1
,A
2
,⋯,A
n
} is said to be greater than sequence {B
1
,B
2
,⋯,B
m
} if there exists 1≤k<min{n,m} such that A
i
=B
i
for i=1,⋯,k, and A
k+1
>B
k+1
.
Sample Input:
20 9 24
10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2
00 4 01 02 03 04
02 1 05
04 2 06 07
03 3 11 12 13
06 1 09
07 2 08 10
16 1 15
13 3 14 16 17
17 2 18 19
Sample Output:
10 5 2 7
10 4 10
10 3 3 6 2
10 3 3 6 2
Special thanks to Zhang Yuan and Yang Han for their contribution to the judge's data.
#include <iostream>
#include <vector>
#include<algorithm>
#include <cmath>
#include<map>
#include<cstring>
#include<queue>
#include<string>
#include<set>
#include<stack>
using namespace std;
typedef long long ll;
const int maxn=110,inf=100000000;
vector<int>v[maxn];int n,m,s,weight[maxn],path[maxn];
bool vis[maxn]={0};
bool cmp(int a,int b){
return weight[a]>weight[b];
}
void dft(int idx,int dep,int sum){
sum+=weight[idx];
if(sum>s) return;
if(sum==s) {
if(v[idx].size()) return;
cout<<weight[0];
for(int i=0;i<dep;i++) cout<<" "<<weight[path[i]];cout<<endl;
return;
}
for(int i=0;i<v[idx].size();i++){
path[dep]=v[idx][i];
if(v[idx][i])
dft(v[idx][i],dep+1,sum);
}
}
int main(){
cin>>n>>m>>s;
for(int i=0;i<n;i++) cin>>weight[i];
for(int i=0;i<m;i++){
int fa,cnt,child;
cin>>fa>>cnt;
for(int j=0;j<cnt;j++){
cin>>child;v[fa].push_back(child);
}
sort(v[fa].begin(),v[fa].end(),cmp);
}
dft(0,0,0);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号