拓扑排序

　　从今天开始写博客，记录下平常遇到的一些问题，第一篇博客就献给拓扑排序吧。

　　为什么要对图进行拓扑排序？最初遇到这个问题是在计算图中最长的路径的长度时遇到的，对图进行拓扑排序之后就可以比较方便的计算最长路径了。

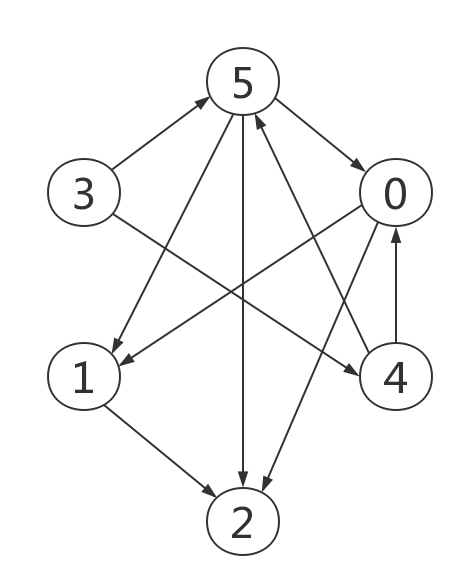
　　对一个有向无环图（DAG）进行拓扑排序，通俗地讲，是将节点排成“一行”，对于图中任意一条边uv（方向由节点u指向节点v），在这行中，节点u的位置总是在节点v的左边。例如对于下图，它的一种拓扑排序的结果是3，4，5，0，1，2. 拓扑排序的结果有很多，不止这一种。

　　拓扑排序用的是DFS，但是进行了点改动。在DFS中，访问并打印当前节点后，继续对当前节点的邻接节点执行DFS。而在拓扑排序中，我们维护一个栈，访问当前节点了，只有在当前节点的所有邻接节点都在栈里时，我们才把节点加到栈里，然后对邻接节点执行DFS和同样操作，直到所有节点都被访问。最后，把栈里的节点一个个取出，最先取出的节点就是拓扑排序的“头”。

　　以上图为例，假设从0开始做DFS。

　　访问0，0的邻接节点1和2还不在栈里，所以不添加节点到栈，栈为【】。

　　访问1，2还不在栈里，不添加节点进栈，栈为【】。

　　访问2，依次添加2，1，0进栈，栈为【2，1，0】。

　　访问3，不添加节点进栈，栈为【2，1，0】。

　　访问4，5还不在栈里，不添加节点进栈，栈为【2，1，0】。

　　访问5，依次添加5，4，3进栈，栈为【2，1，0，5，4，3】。

　　将节点依次从栈里取出，拓扑排序顺序为3，4，5，0，1，2.

　　拓扑排序要求图中没有环，导致它在实际应用中有局限性。用现实数据构建的图往往存在大量的环，例如投资关系里的环，A投资B，B投资C，C投资A就构成了一个环。另一方面，拓扑排序在任务调度上还是挺有用的，任务的调度关系构建的图是DAG的情况比较多。

　　该算法时间复杂度为O(V+E)，还有一个使用入度来进行拓扑排序的算法（Kahn算法），时间复杂度也能达到O(V+E)。

from collections import defaultdict

class Graph:
    def __init__(self, vertices):
        self.graph = defaultdict(list)  # 用一个字典存储每个节点的邻接节点list
        self.V = vertices  # 节点个数

    def addEdgeList(self, pairs):
        for (u, v) in pairs:
            self.addEdge(u, v)

    def addEdge(self, u, v):
        self.graph[u].append(v)

    def topologicalSortUtil(self, v, visited, stack):
        # 递归函数
        # 标记当前节点为已访问
        visited[v] = True
        # 对该点的邻接节点继续调用topologicalSortUtil()
        for i in self.graph[v]:
            if visited[i] == False:
                self.topologicalSortUtil(i, visited, stack)
        # 将当前节点加入栈里
        stack.insert(0, v)

    def topologicalSort(self):
        # 递归调用topologicalSortUtil() 来实现拓扑排序
        # 初始状态，标记所有节点为未访问
        visited = [False] * self.V
        stack = []
        # 对所有节点，one by one，如果它没被访问，就执行topologicalSortUtil()
        for i in range(self.V):
            if visited[i] == False:
                self.topologicalSortUtil(i, visited, stack)
        # 打印结果
        print(stack)

if True:
    g = Graph(6)
    edge_list = [(0, 1), (0, 2), (1, 2), (3, 4), (3, 5), (4, 5), (5, 0)]
    g.addEdgeList(edge_list)
    g.topologicalSort() # [3, 4, 5, 0, 1, 2]