python语法技巧——学习笔记（一）

从cs231n作业中看到的简洁高效语句。

• Reshape the image data into rows

X_train = np.reshape(X_train, (X_train.shape[0], -1))

 

• xrange用法与 range的区别

用法完全相同，所不同的是xrange生成的不是一个list对象，而是一个生成器。要生成很大的数字序列的时候，用xrange会比range性能优很多，因为不需要一上来就开辟一块很大的内存空间。

所以尽量用xrange代替range。

 

• np.linalg.norm()

linalg = linear + algebra，线性代数

norm表示范数，x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False) 

①x: 表示矩阵（也可以是一维）

②ord：范数类型

向量的范数：

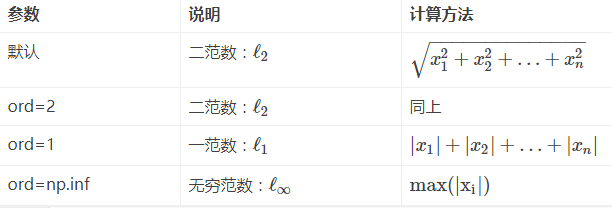
矩阵的范数：

ord=1：列和的最大值

ord=2：|λE-ATA|=0，求特征值，然后求最大特征值得算术平方根

ord=∞：行和的最大值

③axis：处理类型

axis=1表示按行向量处理，求多个行向量的范数

axis=0表示按列向量处理，求多个列向量的范数

axis=None表示矩阵范数。

④keepding：是否保持矩阵的二维特性

True表示保持矩阵的二维特性，False相反

 

• flatnonzero()

该函数输入一个矩阵，返回扁平化后矩阵中非零元素的位置（index）
这是官方文档给出的用法，非常正规，输入一个矩阵，返回了其中非零元素的位置

>>> x = np.arange(-2, 3)

>>> x
array([-2, -1,  0,  1,  2])
>>> np.flatnonzero(x)
array([0, 1, 3, 4])

• numpy中的broadcast广播机制

实例：[[1,2]] + [[1], [2]] =[[1,1], [2,2]] + [1,2], [1,2]] = [[1,3], [3,4]]
执行 broadcast 的前提在于，两个 ndarray 执行的是 element-wise（按位加，按位减） 的运算，而不是矩阵乘法的运算，矩阵乘法运算时需要维度之间严格匹配。

  当操作两个array时，numpy会逐个比较它们的shape（构成的元组tuple），只有在下述情况下，两arrays才算兼容：

1. 相等
2. 其中一个为1，（进而可进行拷贝拓展已至，shape匹配）

 

• np.bincount()

    它大致说bin的数量比x中的最大值大1，每个bin给出了它的索引值在x中出现的次数。

   例如：>> x = np.array([1, 2, 1, 2, 3, 5, 6,1])

    >> np.bincount 

    bin有7个，0-6，索引0出现,0次，1出现了3次，2出现了2次……

   >> [0, 3, 2, 1, 0, 1, 1]

 

• np.argmax(a, axis=None, out=None)

    返回沿轴axis最大值的索引。

    结合np.bincount()， np.argmax(np.bincount(x))，可以得到list x中出现次数最多的数字是几。