Codeforces Round #757 (Div. 2) - D1. Divan and Kostomuksha (easy version)

Codeforces Round #757 (Div. 2) - D1. Divan and Kostomuksha (easy version)

比赛链接：Codeforces Round #757 (Div. 2)

题目链接：https://codeforces.com/contest/1614/problem/D1

官方题解：https://codeforces.com/blog/entry/97283

大佬题解：知乎 - pzr - Codeforces Round #757 (Div. 2) A~D1

题意：

求式子的最大值：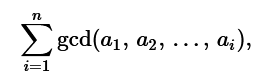

题解：

状态转移方程：dp[j] = max(dp[j], dp[i]+(j-i)*num[j])

dpi是以i为序列开头的gcd的最大值，j是i的倍数

num[j] 是序列中以j为因子的数的个数

dpj与dpi的差就是序列前面gcd为j的部分

代码：

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef long double ld;

const int N = 5e6;
ll dp[N+10], num[N+10], n, x[N+10];

void jud(){
    for(int i = 1; i <= N; i++)
        for(int j = 2*i; j <= N; j += i)
            num[i] += num[j];
}
bool cmp(ll a, ll b){
    return a > b;
}
int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);

    int n; 
    cin>>n;
    for(int i = 1; i <= n; i++) cin>>x[i], num[x[i]]++;
    jud();
    dp[1] = n;
    ll s = 0;
    for(int i = 1; i <= N; i++)
        for(int j = 2*i; j <= N; j+=i)
            dp[j]=max(dp[j], dp[i]+(j-i)*num[j]);
    
    sort(dp+1,dp+1+N,cmp);
    cout<<dp[1]<<endl;

    return 0;
}