基础图论学习笔记

有向图：有方向的图，及边 \((u, v)\) 只能从 \(u\) 到 \(v\)，而不能从 \(v\) 到 \(u\)。

无向图：不规定方向的图，及边 \((u, v)\) 既能从 \(u\) 到 \(v\)，也可以从 \(v\) 到 \(u\)

连通：存在路径从 \(u\) 到 \(v\) ，那么这两个点就是连通的

连通图：任意两点都连通的图叫做连通图

简单图：不含重边和自环的图称为 简单图

负环：长度为负数的环称为 负环

路径长度：路径上每条边的权值之和称为 路径长度

最短路：称 \(v\) 到 \(u\) 的 最短路 为最短的连接 \(v\)到 \(u\) 的路径

图的存储

邻接矩阵

比如说这样一张有向图，我们给他用邻接矩阵存储

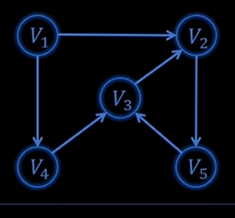
因为v1和v2直接有一条道路，所以 \(map[1][2]\) = 这一条边的边权，如果没有则为1

v1和v4直接有一条道路，所以 \(map[1][4]\) = 1;

以此类推，直到将所有边都给存入

无向图则是 \(map[1][2]\) = \(map[2][1]\) = 这一条边的边权

相当于两条有向图的边

空间复杂度为 \(O(n^2)\)，也就是说如果我们有1e5个这种点，空间就会爆掉

而且我们的边不一定会有这么多，也就是说会有很多浪费的空间

所以，vector出手了

邻接表

邻接矩阵因为vector直接进化成邻接表

我们可以先定义一个vector数组 \(a[n]\)

v1和v2直接相连，a[v1].push_back(v2)，表示可以从v1直接到达v2

v1和v4直接相连，a[v1].push_back(v4)，表示从v1可以直接到达v4

v2和v5直接相连，a[v2].push_back(v5)，表示从v2可以直接到达v5

以此类推

这样我们的空间复杂度就只有 \(O(m)\)，比以前的 \(O(n^2)\) 要优化了不少

链式前向星

链式前向星类似于链表，以边为基本单位，记录了每条边的情况。

链式前向星主要用了三个数组，一个是head，一个是edge，还有nxt。

edge记录边，head记录头，head[i]表示第i个链表的头结点位置，nxt表示下一个边的位置。

模板：

void add_edge(int x, int y, int z) {
	//连接从x -> y的边，z为边权 
	nxt[++ cnt] = head[x]; 
	//更新下一个结点 
	head[x] = cnt;
	//更新头节点 
	edge[cnt] = z;
}

理解起来比较复杂。

图的遍历

这个不用说了吧，dfs或bfs即可，特别简单。

实在不懂的话可以看这两个视频：

dfs遍历图

bfd遍历图

最短路

弗洛伊德算法

弗洛伊德是专门求所有点互相之间的最短路径的算法，时间复杂度为 \(O(n^3)\)

弗洛伊德算法主要是运用邻接矩阵来存图，比如说下面这个：

表中的13代表从0到2的权值是13

无穷代表不存在从2到1的边

从自身到自身的边权为0

类似于dp 使用三层循环，第一层枚举起点，第二层枚举终点， 第三层循环枚举中转点，及 \(dp[i][j] = \min(dp[i][j], dp[i][k] + dp[k][j])\)。

通过这样就可以求出从 \(i\) 到 \(j\) 的最短路

模板：

#include <stdio.h>
#define inf 0x3f3f3f3f
int map[1000][1000];
int main()
{
    int k,i,j,n,m;
    //读入n和m，n表示顶点个数，m表示边的条数
    scanf("%d%d",&n,&m);
    //初始化
    for(i=1; i<=n; i++)
        for(j=1; j<=n; j++)
            if(i==j)
                map[i][j]=0;
            else
                map[i][j]=inf;
    int a,b,c;
    //读入边
    for(i=1; i<=m; i++)
    {
        scanf("%d%d%d",&a,&b,&c);
        map[a][b]=c;
		map[b][a]=c;//这是一个有向图
    }
    for(k=1; k<=n; k++)
        for(i=1; i<=n; i++)
            for(j=1; j<=n; j++)
                if(map[i][j]>map[i][k]+map[k][j] )
                    map[i][j]=map[i][k]+map[k][j];

    //输出最终的结果,最终二维数组中存的即使两点之间的最短距离
    for(i=1; i<=n; i++)
    {
        for(j=1; j<=n; j++)
        {
            printf("%d ",map[i][j]);
        }
        printf("\n");
    }
    return 0;
}

dijkstra 算法

dijkstra算法的时间复杂度为 \(O(n ^ 2)\)

dijkstra算法的主要特点是从起始点开始，采用贪心算法的策略，每一次遍历到起始点距离最近的点进行拓展，直到拓展到终点为止

算法实现：

有一个起始点为 \(V1\)，终点为 \(V11\) 的图：

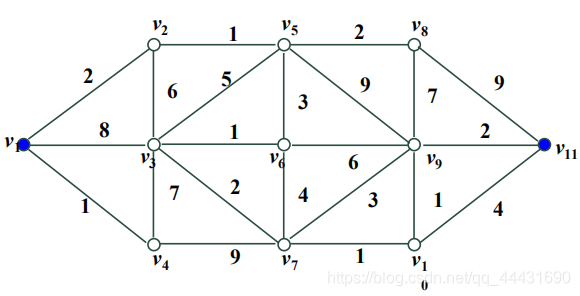
初始化

令所有点到达起点的距离为无穷大，将起点到起点的距离设为 \(0\)

过程

• 找到离起点最近却没有访问过的点
• 更新和这个点直接相连的点所有点的距离，如果距离比原来的距离大，则不更新该点到起始点的距离
• 将这个点标记为访问过，下次不用访问了

将所有节点都访问一遍后，输出