由顶点坐标计算任意多边形面积

我们知道，如果三角形的一个顶点在原点，另两点A（x1 , y1）和B（x2 , y2）

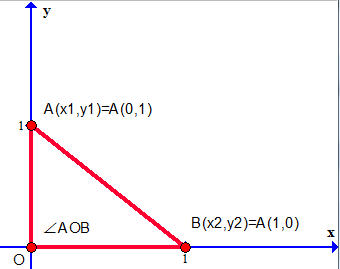
则其面积可以表示为
S_ABC =0.5× |OA|×|OB|×sin（∠AOB）
=0.5×|OA×OB|
=0.5×|(x1,y1)×(x2,y2)|
=0.5×[(x1y2)-(y1x2)]

以下图中的三角形ABC为例，欲求S_ABC

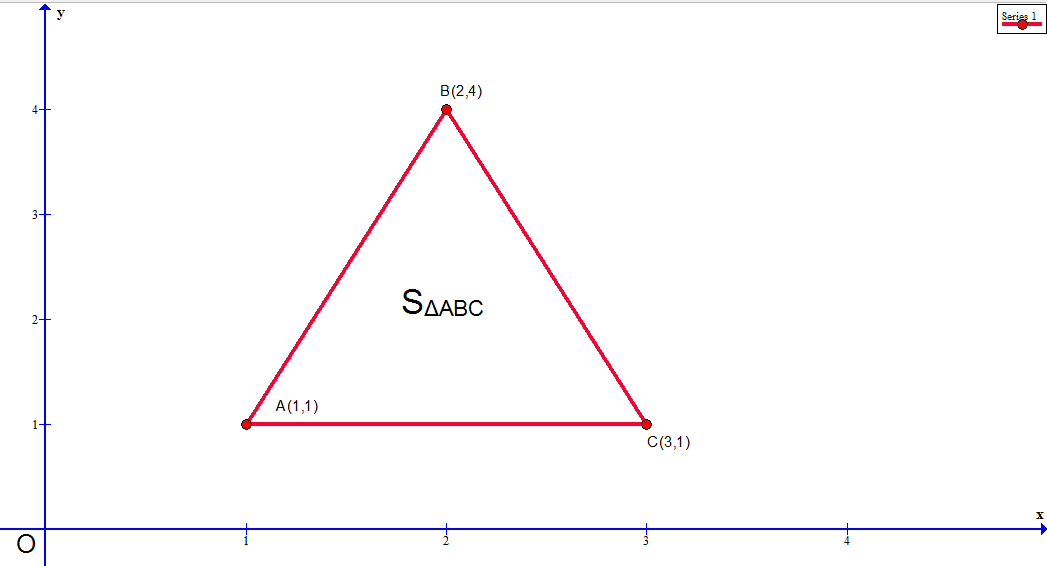
从原点，将ABC以向量形式表示

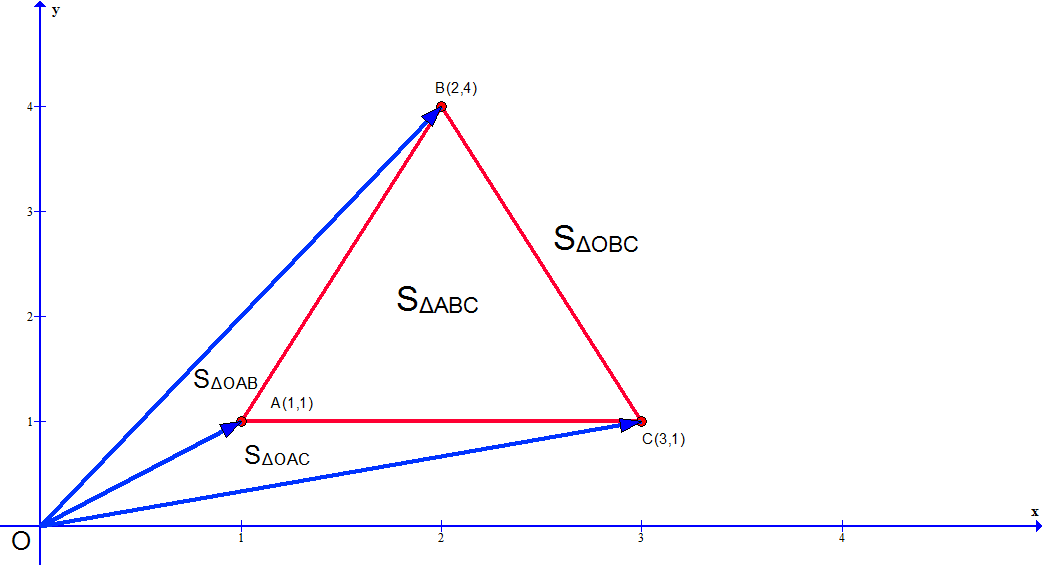
因此S_ABC = S_OBC-S_OAC-S_OAB
=S_ABC = S_OBC + (-S_OAC) + (-S_OAB)

这样直接求ABC的面积转化为了求三个部分三角形的面积和，而分割出来的每个三角形的都有一个顶点为原点，且另外两个点信息均已知。

由于存在逆时针计算或者顺时针计算顶点的问题，所以上式中的正负号代表了正面积和反面积，不过不需要特别考虑，因为总大小是一样的，只需要求绝对值即可。

所以上述三角形面积
SABC=0.5×|(x1y2-x2y1)+(x2y3-y2x3)+(x3y1-y3x1)|

扩展到多边形
S = 0.5×|(x1y2-x2y1)+(x2y3-y2x3)+(x3y4-y3x4) + ...... + (xny1-ynx1)|

对于凹多边形也适用，凹陷的部分会被计算为负面积被减掉。

练习题：HDU2036