图论杂题选做

MinOr Tree

题意

给你一个图，让你求他或运算下的最小生成树。

题解

好题。我们令答案为 \(ans\)，那么对于 \(ans\) 的每一位，从高往低我们肯定能取 \(0\) 就取 \(0\)，证明是显然的。那么怎么判断能否取 \(0\) 呢？

因为是或运算，如果答案是 \(0\)，那么这个生成树的每一个权的这一位也都是 \(0\)，我们先把这一位是 \(1\) 的去掉，看剩下的是否联通。如果联通那么这一位就取 \(0\)，如果不连通，我们就把刚才删掉的边加回来，然后取 \(1\)。

code

submission。有点卡常。

---

Toss a Coin to Your Graph...

题意

珂朵莉给了你一个有向图，边数最大 \(2 \times 10^5\)，每个点有一个点权，任选起点，走 \(k, k \le 10^ {18}\)步，问经过的点的最大权值最小能是多少？，无解输出-1，没有重边和自环，但是会有环。

题解

我们对照图分析他的性质。

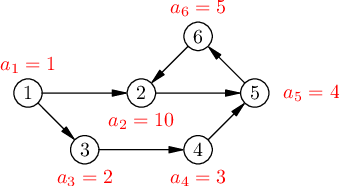
假定我们现在走过的路的点权一定是小于一个值的，我们叫他新图。那么如果我们走到了一个环里，那肯定是合法的。因为我们只需要不断的绕圈子走完这 \(k\) 步即可。

那么没有环呢？我们跑一遍最长路，如果新图中最长的路径是小于 \(k\) 的，说明我们如果要走完这 \(k\) 步，肯定要走一部分老图，但老图点权都是不合法的，所以不可取，反之成立。

对于最长路和判环，我们可以拓扑加 \(\tt{DAGDP}\) 解决。

然后回到我们最初的问题，如何确定那个最小的点权呢？注意到题目中是最大值最小，那么显然二分了。

注意千万不要用 \(\tt{map}\)！！queueforces 对这个非常敏感。

code

submission。

---

通往奥格瑞玛的道路

题意

在艾泽拉斯，有 \(n\) 个城市。编号为 \(1,2,3,\ldots,n\)。城市之间有 \(m\) 条双向的公路，连接着两个城市，从某个城市到另一个城市，会遭到联盟的攻击，进而损失一定的血量。每次经过一个城市，都会被收取一定的过路费（包括起点和终点）。路上并没有收费站。假设 \(1\) 为暴风城，\(n\) 为奥格瑞玛，而他的血量最多为 \(b\)，出发时他的血量是满的。如果他的血量降低至负数，则他就无法到达奥格瑞玛。歪嘴哦不希望花很多钱，他想知道，在所有可以到达奥格瑞玛的道路中，对于每条道路所经过的城市收费的最大值，最小值为多少。

题解

和上一题非常像，很明显二分，然后跑一遍最短路。注意边界！\(l = max(f_1,f_n)\), \(r=max_{i=1}^nf_i\)，然后就做完了。

code

submission。

---

【GXOI/GZOI2019】 旅行者

题意

有一个图，给你特定的 \(k\) 个城市，求这 \(k\) 个城市两两最短路的最小值。时间限制是 \(5.00s\)。

题解（随机化算法）

有一个很显然的做法就是对于每一个点跑最短路，这样时间复杂度很高，我们考虑优化。

\(k\) 个点。我们不难想到有一种见图技巧就是多个起点我们建立一个超级源点来处理，这给了我们一点启发。我们可以将这 \(k\) 个点分成两个组，一个组建立一个超级起点，一个建立一个超级重点，然后跑 一遍 最短路，那么这样错误率是 \(25\%\) 的，我们跑 \(20\) 次，时间绰绰有余，而且错误率降到了 \(0.1\%\)。

这样这题就解决了。注意初始值开大一点，随机数安全一点。

code

submission。

---

【HAOI2016】 食物链

题意

给你一个食物网，求食物链条数。

题解

太简单，不说了。放在这里证明我做过了。

code

submission。