CF Round题解&记录
- CF1581 (#746) div2
- CF1592 div2
- CF1594 div2
- CF1598 div2
- CF1586 div1+2 (#749)
- CF1582 div2 #750
- CF1606(edu
- CF1604 div2 #752
- CF1608
- CF1615
- CF1625 div2(#765)
- CF1628 div1(#767)
- CF1630 div1(#768)
- CF1633 edu(#122)
- CF1638 div2(#771)
- CF1635 div2(#772)
- CF1644 div2(Edu123)
- CF1641 div1(#773)
- CF1648 div1
- CF1654 div1+2
- CF1699 div2
- CF1702 div3
- CF1704 div1+2
- CF1713 div2
- CF1746 global
大致按时间排序。
CF1581 (#746) div2
A
你考虑为什么是数 >=n 而不是 >n。显然你把一个答案为 i 的排列倒过来,它的答案就是 2n-i 了,所以这是一个 <n 到 >=n 的双射。同时答案范围为 \([0,2n-1]\),所以数量就是对半分的 \(\frac{n!}{2}\)
B
连通图,先考虑生成树。如果这棵树的高度为 2 那么直径就是 <=2 的。同时直径 =1 当且仅当其为完全图。然后大力分类讨论就做完了,本场最垃圾题。
C
reachable
经典套路,固定上下两边,高效维护横轴的信息。
D
medium+
对于 \(1\sim i\) 的排列,考虑其最大值 \(i\) 在哪个位置。如果 \(i\) 在位置 \(w\),那么左边就变成了 \(n=w-1,m=m-1\) 的版本,右边就变成了 \(n=i-w,m=m-1\) 的版本
这样并不能转移,再加一维 \(k\) 表示好数有 \(k\) 个的方案数,然后枚举左边贡献多少个好数,这样是 \(O(n^5)\) 的。具体地,令 \(f(i,j,k)\) 表示 \(n=i,m=j,k=k\) 时的答案,那么 \(f(i,j,k)=\sum f(w-1,j-1,t)\cdot f(i-w,j-1,k-(j==1)-t)\cdot \binom{i-1}{w-1}\)
初始化和卡常一堆细节,感谢切队指导。有一个挺重要的点是对于 \(j>i\),\(f(i,j,0)\) 应当初始化为 \(i!\)。还有一个很有力的常数优化是如果 \(f(w-1,j-1,t),f(i-w,j-1,k-(j==1)-t)\) 中有一个值为 \(0\) 那就不要转移。
E
reachable
周期性,DS 相关,可以去想根号分治。令 s[i]=x[i]+y[i],T=sqrt(m)。如果 s[i]>T 则分成 m/T 段区间加,差分;如果 s[i]<T,注意到时刻 j 是否受到这辆车影响仅与其 %s[i] 的结果有关, 所以可以分别维护 2~T 意义下的同余系,对每个同余系暴力修改 j%p=x 时处于多少辆车的影响下即可。注意处理 (i-j+mod)%mod 时一定要先令 i$=mod,j%=mod!!!
F
思路 easy
笛卡尔树上启发式分裂,其实复杂度仍然是 \(O(n^2)\) 的
CF1592 div2
暴打自己痛点的一场
A
略
B
reachable
一个经典问题:给定一个数组,每次可以从给定的位置对中选择一对位置并交换这两项,问能否使这个数组不降。
建图连边,每个连通块均可以自由重排,暴力把每个连通块对应的元素排序再放回原数组,然后判断是否满足要求。
回到本题,所有满足 \(|a-b|\ge x\) 的 \(a,b\) 都会有一条连边,手模一下就会发现只有 \([n-x+1,x]\) 这段区间的点是孤零零的,其余的点构成了一个整的连通块。因此只需要判断原数组的 \([n-x+1,x]\) 和排序后的数组是否一致(如果 \(n-x+1>x\) 那么肯定有解)。
C
reachable
题意:给定一棵树,最少断 \(1\) 条边,最多断 \(k-1\) 条边,问有没有可能使得到的连通块的点权异或和均相同。
好像也是一个经典套路?只需要考虑断 \(1\) 条和断 \(2\) 条的情况。先把断边转为断点,第一种情况对应所有点点权异或和为 \(0\),枚举子树即可。第二种每个连通块的异或和一定等于所有点的异或和,设为 \(w\)。考虑两个断点 \(x,y\) 的祖孙关系。不妨令 \(dep_x<dep_y\),\(val_x\) 表示 \(x\) 的子树异或和。如果 \(x\) 是 \(y\) 的祖先则必须满足 \(val_y=w,val_x=0\),否则必须满足 \(val_x=val_y=w\)。于是就可以 dfs 统计每个点儿子的子树信息,分 \(val\) 讨论。
D
reachable
欧拉序每段区间对应的都是一个连通块,因此可以在欧拉序上二分。
dfs 序左端点为 \(1\) 的所有区间对应的也都是一个连通块,因此可以在 dfs 序上倍增右端点!(max 包含不影响)常数小一倍
E
reachable
一些数 & 起来比 ^ 大,等价于存在第 \(i\) 位,这一位上全为 \(1\) 且数的个数为偶,更高位异或的结果为 \(0\)。枚举 \(i\),对于每个前缀异或和开桶。
CF1594 div2
A&B 略
C
easy
如果答案 >=2,先来一次 \(x=n\) 再来一次 \(x=n-1\) 一定可行。于是只需要判掉答案 \(<2\) 的情况。
若 \(s\) 已经满足条件,答案为 \(0\),否则把所有 \(s_i\not=c\) 的 \(i\) 拎出来,如果存在一个 \(x\in[1,n]\) 使得 \(\forall s_i\not=c,x\nmid i\)。直接开桶+调和级数即可。
D
easy
\(i\) 说 \(j\) 为假,若 \(j\) 为假则 \(i\) 为真,\(j\) 为真则 \(i\) 为假;\(i\) 说 \(j\) 为真,若 \(j\) 为真则 \(i\) 为真,\(j\) 为假则 \(i\) 为假。
用异或来描述,如果 \(i\) 说 \(j\) 为假则在 \(i,j\) 之间连一条边权为 \(1\) 的无向边, \(i\) 说 \(j\) 为真则连一条边权为 \(0\) 的无向边。对于每个连通块,只要有一个点的真/假确定了那么其余点也就随着确定了。对每个连通块进行 dfs 二染色即可,注意判无解!
E
medium+
E1 是说,你要给一棵深度为 \(k\) 的满二叉树染色,同色和对色不能相邻(对色是指标准魔方相对两面的颜色),问方案数。首先可以 dp,不过那就绕弯路了。根结点有 \(6\) 种选择,根结点的颜色确定之后自顶向下确定,每个结点有且仅有 \(4\) 种选择,因此答案为 \(6\times 4^{2^{k}-2}\)。
E2 则是先钦定了 \(n\) 个结点的颜色,问合法方案数。我们称一个结点为关键点,当且仅当它的颜色被钦定或它是某个被钦定点的祖先。由 E1,不难发现非关键点的贡献是平凡的 \(4\),而关键点均在被钦定点到根的路径上。由于 \(k\) 很小,所以关键点的数量不会很多,不妨保留所有关键点,这些关键点形成了一棵新树,我们在新得到的树上做树形 dp 即可,复杂度 \(O(36kn)\)。
F
amazing-
很神奇的贪心。我们要做的其实是尽量构造一个序列,使得其不存在一个和为 \(k\) 的连续子段。考虑插板法的思路,现在有 \(s\) 个球 \(s+1\) 个空隙,其中第 \(0,s\) 个空隙必须选,我们需要从 \(1\sim s-1\) 这些空隙里选出 \(n-1\) 个空隙,使得它们两两间的距离不为 \(k\)。
先转为最多能选多少个空隙,显然位置膜 \(k\) 不同余的空隙是相互独立的,把膜 \(k\) 同余的空隙抽出来组成 \(k\) 条数轴,我们要做的就是对每条数轴上的点赋值 \(0/1\),要求 \(1\) 与 \(1\) 不能相邻,问最多有多少个 \(1\)。贪心,每条数轴肯定是 \(1010101\) 这样交替选,但由于第 \(0\) 个空隙和第 \(s\) 个空隙已经被钦定了,所以它们所在的数轴要进行一些调整,不过这些调整对于数量是不会有影响的:首先如果它们所在数轴的长度为奇数那么无影响;否则,如果 \(0\) 和 \(s\) 不在同一条数轴上(即 \(k\nmid s\)),那么只需要把 \(01\) 取反,在同一条数轴上(即 \(k\mid s\) )只需要把最后的 \(10\) 改成 \(01\),比如 \(1010\) 改成 \(1001\) 就没事了。只有一种情况是例外的:\(0,s\) 在同一条数轴上且这条数轴上只有 \(0,s\) 这两个点,这对应 \(k=s\) ,先判掉就行。
综上,我们把原问题等价转化为了若干条独立的数轴上选最多的不相邻的点,给出了最优决策并证明了其正确性。现在来计算答案:如果第 \(i\) 条数轴的长度 \(len_i\) 为偶数,那么答案为 \(\lfloor\frac{len_i}{2}\rfloor\),否则答案为 \(\lfloor\frac{len_i}{2}\rfloor+1\)。有 \(s\%k+1\) 条数轴长度为 \(\lfloor\frac{s}{k}\rfloor+1\),其余数轴长度为 \(\lfloor\frac{s}{k}\rfloor\),对于 \(\lfloor\frac{s}{k}\rfloor\) 的奇偶性分类讨论一下就好了。
题外话:很多人的构造策略可能是先放 \(k-1\) 个 \(1\) 再放 \(1\) 个 \(k+1\) 交替进行。注意到最开始 \(1010101\) 交替选是等价于这个决策的,尽管有些情况下并不一定正确,但它所选出的 \(1\) 的数量一定是正确的(换句话说,一定有其他的决策与其答案相同且没有决策更优),所以根据这个判一下够不够放也是对的。
CF1598 div2
A
可达的充要条件为不存在某一列上下两个格子都为 \(1\)
B
\(O(5\times5)\) 枚举两次课分别设在哪一天,先判掉有学生两天都没有空,然后分三类:只能上第一次课,只能上第二次课,两次课都有空。如果前两类中的任意一类数量大于一半则不行,否则可行。
C
设原平均值为 \(k\),显然删掉的两个数的平均值必须也得等于 \(k\)。问题转为求原序列中有多少对数的和为 \(2k\)。
D
medium+
这样的形式(这是 \(6\) 种可能顺序中的一种)。同样是因为没有二元组完全相同,因此以中间的 \((a,b)\) 为标识计数能做到不重不漏。简单补集转化即可
bonus:如果可能存在两个相同二元组该怎么做?
E
reachable
赛时离正解较近。
赛时想到了维护每条主对角线上的信息,拓展一下,维护每条从左上开始到右下的极长路径就行。单独的格子单独算,然后就 \(O(nq)\) 了……
F
medium
注意到 \(n\) 只有 \(20\),考虑状压 dp。我们定义一种拼接顺序是合法的,当且仅当它不存在一个右括号数大于左括号数的前缀
CF1586 div1+2 (#749)
A
略
B
显然让给定点对的距离越近越容易满足条件,考虑构造一棵深度为 \(2\) 的树,由于点对数 \(<n\),因此一定能找到一个 \(b\) 使得它没有出现过,把它作为根即可。
C
medium+
首先,一个点不能逃脱的前提是以该点为右下角的子矩阵里出现了如下情形:
如果棋盘里出现了这种情况,那么一定有点的状态是不确定的。否则,所有非障碍点都可以逃脱,不能逃脱的点一定是障碍,因此是确定的。问题转化成判断给定的子矩阵中有无上述情形,前缀和即可。
D
amazing-
次数 \(2n\),要求猜出一个序列。这种交互题的思路一般都是先用 \(n\) 次操作确定某一位置的值,然后利用这个已确定的值依次确定其他位置的值。先来解决后半段,假设已知 \(a_i=x\),那我们可以令 \(b_i=y\),其余位置为 \(x\),如果 \(y\) 所在位置在 \(i\) 之前,就可以通过一次询问得到 \(y\) 所在位置。如果 \(i=n\),那就可以通过 \(n-1\) 次操作知道所有位置的值。
现在问题只剩下如何用 \(n\) 次操作确定 \(a_n\) 的值。考虑利用值域进行排除。先令 \(b_n=n,b_{i<n}=1\),询问有解当且仅当 \(a_n=1\)。无解则继续询问,令 \(b_n=n-1\),由于 \(a_n\not= 1\) 因此询问有解当且仅当 \(a_n=2\),以此类推最多询问 \(n\) 次就能确定 \(a_n\),这题就做完了。
E
amazing
图上构造,要求满足奇偶性。这种题先想生成树一般就赢了。令 \(f_v\) 表示 \(v\) 作为路径端点的出现次数,\(g_v\) 表示 \(v\) 连出的边的边权和。
首先,如果存在 \(f_v\) 为奇那么一定没有合法的构造方案,这是因为如果 \(v\) 不是路径的端点那么每一条经过 \(v\) 的路径给 \(g_v\) 带来的变化一定是 \(+2\),而如果 \(v\) 是某条路径的端点,其对于 \(g_v\) 的影响是 \(+1\),因此如果 \(f_v\) 为奇则 \(g_v\) 为奇,不符合要求。
其次,如果所有的 \(f_v\) 均为偶那么一定存在合法的构造方案。考虑在生成树上构造,每个叶子连向父亲的边的边权一定为偶,然后剥掉叶子。由于 \(f_v\) 均为偶,所以 \(g_v\) 为偶,所以新产生的叶子连向父亲的边的边权也一定为偶……以此类推,得证。
综上,一张图有合法方案的充要条件是 \(f_v\) 均为偶。如果不满足条件,所需要添加的最少路径数为满足 \(f_v\) 为奇的 \(v\) 的数量除以 \(2\)。由于一条路径会令两个 \(f\) 值加 \(1\),因此奇点的个数必为偶,可以整除。
F
medium
zr 原题。按 k 分块,叠下去就好了(tyy:这是我这个月第三次见到这种套路了)
CF1582 div2 #750
A
amazing--
奇妙。结论是所有分配方式能取到 \([0,a+2b+3c]\) 里的每一个值。只会感性理解,不会直观证明
另一个更弱的结论是一定存在一种方案使得两边差的绝对值小于等于 \(1\)。这个就先均分 \(3\),差值只可能为 \(0,3\),然后放 \(2\),差值只可能为 \(0,1,2\)(2 的情况是 3 恰好能对半分),最后放 \(1\) 就能把差值控制在 \([0,1]\) 内。
B
略
C
reachable
枚举要删的字符 c,开左右两个指针向里面扫,如果遇到一对不同的位置就必须删一个 c(都不是 c 就无解),这是因为如果不删的话这一对始终都是对应位置(回文的性质很强)。这样做是 \(O(|S|n)\) 的,\(|S|\) 为字符集大小。
这个做法看上去就有很大的改进空间,事实上真可以优化至 \(O(n)\)。我们还是枚举要删的字符 \(c\),只不过这次用哈希来加速匹配过程。具体地,先删去所有 \(c\),这样原字符串就被分成了若干段子串(段与段之间是连续的 \(c\)),我们对这些段进行双指针匹配,每次用更短的一边抵消更长的一边(哈希判回文,转成正串反串就行)。如果两边恰好匹配那么接下来的 \(c\) 就不必删除,否则必须删除。这样每次循环的复杂度是 \(O(cnt_c)\) 的(\(cnt_c\) 为 \(c\) 的出现次数),合起来就是严格 \(O(n)\)。
D
medium-
大分类讨论题/tuu
E
CF1606(edu
CF1604 div2 #752
C 题又又又又又降智了,直接把自己送出前 50/kx
A
略
B
如果 n 为偶,划分成 n 个长度为 1 的段即可
否则,如果存在 \(a_i\ge a_{i+1}\) 则把 (i,i+1) 划在一起,其余同上。
不存在的话,相当于是把 \(n\) 分成若干个正整数之和使得这些正整数的异或和为 0。由于 n 为奇,所以最低位的异或和一定不为 \(0\),无解
CF1608
A
垃圾题
B
垃圾分讨
C
好题。
注意到,如果我能打败 a,那我就能打败 a 能打败的所有人——这是一个图论可达性结构
直接 tarjan,缩点后的零度点即为 win,否则 lose。
D
好题,但是 C 卡太长时间没来得及写。
注意到一个染色方案合法等价于 WW 和 BB 的数量相同。必要性考虑从全为空白的骨牌开始染色,那么 W 和 B 的数量一定相同,也就是说 WW 和 BB 的数量相同,充分性考虑倒推(如果 WW 和 BB 数量为 0 的话则不能填成 WB BW 的形式)。
首先忽略掉已经被确定为 \(WB\) 或 \(BW\) 的骨牌。有 \(O(n^2)\) dp:令 \(f(i,j)\) 表示前 \(i\) 个骨牌已确定,\(WW-BB=j\) 的方案数。则:
第一种转移对应 \(s_i=??\) ,第二种对应 \(s_i=W?,?W\),第三种对应 \(s_i=B?,?B\),第四种对应 \(WW\),第五种对应 \(BB\)。我们可以把 \(f_{i-1}\rightarrow f_{i}\) 的转移看做一个整体,即对一个序列本身做一个变换。那么第一种转移相当于先做一次第二种转移再做一次第三种;第四种和第五种则分别是右移和左移,第三种操作又相当于先做一次第二种转移再左移一位。于是我们所有的转移都变成了第二种转移和左移右移。观察第二种转移,它其实就是杨辉三角,因此最终答案为一个组合数,这样就能 \(O(n)\) 求解了(还要减去没有 \(WW,BB\) 的特殊情况)。
CF1615
拿大号打,终于上大分了。感觉这场题目质量都还不错?
A
略
B
显然有一个不用脑子的 \(V\log V+T\log V\) 预处理做法,但是赛时愚蠢的我脑子坏掉了,整出来个 \(T\log^2V\) 的做法。具体地,我们求出 \([l,r]\) 这个区间里每一位上的 \(1\) 的数量,先拆成两个前缀相减,对于每个前缀 \([1,x]\),考虑每个 \(i\) 是在第几位与 \(x\) 不同然后计数。
C
注意到相邻两次操作相当于把 \(s\) 中的一个 \(0\) 和一个 \(1\) 交换,分偶数次和奇数次操作讨论。奇数次的话枚举对哪一位操作,动态更新答案
D
好题,树上异或路径,啪的一下先转成异或前缀和……然后呢?
考虑把一个 -1 变成 \(x\) 对异或 popcount 的影响,你惊讶地发现这个影响也只与 \(x\) 的 popcount 的奇偶性有关!
于是就可以按照 popcount 的奇偶性把题意变为 \(n\) 个 \(0/1\) 变量的异或关系,直接 2-SAT,赢麻了!!1
事实上你也可以二分图染色,更为高明,但赛时的我脑子又双叒叕坏掉了/hanx
E
好题,感觉比 D 稍简单?
\(w(r-b)\) 有三个变量,不好!化成 \((n-r-b)(r-b)=nr-r^2+b^2-nb\),只有 \(r,b\) 这两个变量了!
而且这个形式非常简明!恰好是两个关于 \(x\) 轴对称的二次函数。如果固定 \(b\),\(r\) 越接近 \(\frac{n}{2}\) 对于 red 越优;固定 \(r\) 同理。于是双方的目标就变成了在让自己颜色数量接近 \(\frac{n}{2}\) 的同时最小化对方的颜色数量。枚举 red 的颜色数量,很显然他先把叶子染成红色是最优的(这可以最小化 blue 的颜色数量),你发现这个东西变成了若干条链的并的形状。每次多选一个叶子的收益是这个叶子所在链中还没有被覆盖的部分。
对于每个结点求出它的长链,拿堆动态维护即可。
CF1625 div2(#765)
赛时降智没做出来 D……
ABC 都是简单题
D
唔,先放到 trie 树上看一看。
假设 \(k\) 的最高位为 \(p\),那么 trie 树上高度为 \(p\) 的结点的子树相互独立,而每个高度为 \(p\) 的结点的左儿子的子树里最多选一个,右儿子的子树里也最多选一个,问题转为能否从左子树和右子树里选出两个使其异或 \(\ge k\)。
直接暴力找出左子树里的所有元素,对于每个元素在 trie 树上贪心找到与它异或起来最大的数,看看两者的异或是否 \(\ge k\)。时间复杂度 \(O(n\log n)\)。
CF1628 div1(#767)
vp 了 div1,如果 T1 果断点上线段树就赢麻了……
A
贪心思路是每次选最靠左的与 mex[n] 相同的位置对应的前缀删去。
于是可以直接采用洛谷 P4137 mex 的思路,用一棵线段树维护所有位置的 mex 及其最大值,每次线段树二分找出删到的位置 pos。
事实证明这个线段树做法非常好写也好调,只用了十来分钟就完工了……
还有一个较为简明的线性做法是,用 deque 维护每个值的位置序列,每次按值从小到大遍历直到遇到某个空的 deque,这个 deque 对应的即为 mex。然后考察每个在 mex 之前的 deque 的第一个元素,把它们取 max 就是要删到的 pos,弹出 <=pos 的数即可。注意可能会遇到第一个就为空的情况(即 mex=0),所以你还要顺便记一下当前原序列中还剩多少个数没删。
B
呃,逗你玩题。
如果有长度为 1 的串直接 Yes。否则最多只会选两个串拼起来。为什么?你考虑假设 \(s_i\) 长度为 \(2\) 而且它后面拼接了多个串,那么末尾串长度为 \(2\) 的后缀一定能和 \(s_i\) 构成回文串。由于长度最大为 \(3\),所以只保留 \(s_i\) 和末尾串一定也是合法的。\(s_i\) 长度为 \(3\) 时同理。然后你直接上 map,做完了/cy。
C
神仙构造,不会现在看题解会了。
啥也不说了,考虑把奇数格子和偶数格子分开分别构造:
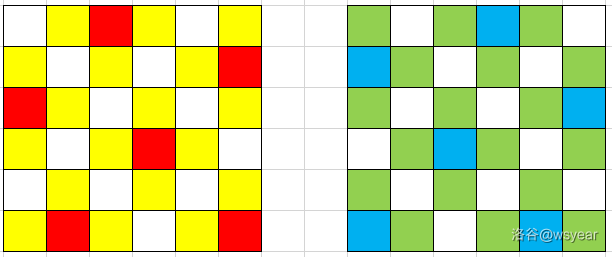
然后就赢了,大眼观察一下发现红色格子和蓝色格子关于整个方格的对称轴对称,红色格子是相隔为 3 的副对角线上相隔为 2 的格子。
实现起来也很简单,直接把每条副对角线包含的格子坐标储存到 vector 里。(话说题解里说这个构造方法很显然,我只能跪拜了orz)
D
emm 这个模型和洛谷 P7137 [THUPC2021 初赛] 切切糕 简直一模一样。写出 dp 式:\(f_{i,j}=\frac{f_{i-1,j-1}+f_{i-1,j}}{2}\),对于 \(0<j<i\) 这个递推式都没问题,特别地(这是由于 \([0,k]\) 这个 bound 的限制),\(f_{i,0}=0,f_{i,i}=ik\)。所以 D1 就直接递推。
分母是平凡的 \(2^{i-1}\),系数也是平凡的 \(k\),考虑只记录分子。dp 式变为 \(f_{i,0}=0,f_{i,j}=f_{i-1,j-1}+f_{i-1,j},f_{i,i}=2^{i-1}\times i\)。看上去阳间多了,如果没有 \(f_{i,0},f_{i,i}\) 的特殊 case 就是一个裸的杨辉三角。所以你考虑抹去这两个 case,找规律不难发现如果令 \(f_{0,i}=0(i\le 0),f_{0,i}=2i-1(i>0)\) 问题就迎刃而解。计算 \(f_{n,m}\) 时考虑 \(f_{0,i}\) 对于 \(f_{n,m}\) 的贡献,这类似于在网格图上走,每次可以向右或右下走一步,问有多少种方案走到 \((n,m)\) 这个点,直接组合数即可。复杂度 \(O(Tm)\)。
CF1630 div1(#768)
很郁闷的一场,BC 场切 500 但就是不会……A 还实现了很久QAQ(不过好在是 vp)
A
做法一
很奇怪的思路。令 A 为全集即 n-1。先对每个 i 配一个 A^i,这样 & 之和就是 0,然后把某些配对断掉再重新配对来调整到 k。注意到如果把 a 和 b 的配对打破重组为 (a,b) 和 (A^a,A^b) 会增加 A^(a^b) 的权值。采用贪心的思路,每次选还没有重组过的增加权值最大且<=k的两个配对进行重组,把 k 减去增加的权值,这样不断循环直到 k=0 或选不出非零的权值组(此时输出-1)。复杂度不会算,为了代码效率采用了链表实现,跑得飞快
做法二
呃其实想到调整之后就可以直接构造了,毕竟 \(k<n\)。
- \(k=0\),不多说
- \(k<n-1\),此时 \(0,A\oplus k\) 不在同一配对里,将其重组即可获得 \(A\oplus(A\oplus k)=k\) 的权值
- \(k=n-1=n-2+1\),把 \(0,1\) 重组,再把 \((2,A\oplus2\oplus 1)\) 重组。特例是 \(n=4\) 时无解,其余情况下 \(2<A\oplus 3<n-2\) 所以构造正确。
B
好题啊好题,属实是把我拿捏了。
先考虑固定了 \([x,y]\) 咋做,如果把在 \([x,y]\) 里的数看做 \(+1\),不在的看做 \(-1\),那么问题变为能否将原数组划分成恰好 \(k\) 个和大于零的连续子段。转为前缀和序列,即是否存在一个长度为 \(k\) 且开头元素 \(>0\) 、以第 \(n\) 个位置为结尾的上升子序列。
dp?不不不,格局太小了。由于数组内的元素只有 \(±1\),所以前缀和序列的变化是连续的。那么,如果某个位置出现了 \(x>0\),那在该位置之前一定存在一个值为 \(x-1\) 的位置。所以以第 \(n\) 个位置为结尾、开头元素 \(>0\) 的最长上升子序列的长度一定等于 \(S_n\),即整个序列元素之和!所以如果全局在 \([x,y]\) 范围内的数比不在其范围内的数多至少 \(k\) 个就一定可以,否则不可以。记录每个值出现的次数尺取 \([x,y]\) 即可。复杂度 \(O(n)\)。
之前 zr 好像也出过类似套路,但那时序列是普通序列,所以只能 dp。值变化连续这个性质还是太强了,以后遇到要多加注意。
C
也是好题,感觉自己对于经典模型与实际问题间的转换还是很生涩……
把每个值出现的位置单拎出来,显然中间的那些都不用管,不平凡的在于第一次出现的位置和最后一次出现的位置。把这些二元组看做线段,那么所有线段的并集减去所有线段的端点一定都能染色,问题在于最多能染几个端点。
首先如果某条线段被其他线段所包含,那这条线段的两个端点先全都染色肯定是不劣的。排除掉这些线段,剩下的线段会形成若干个连通块,每个连通块之间显然独立,所以对每个连通块单独考虑。
我们的策略肯定是先选出若干条线段,用这些线段把其他没选的线段的端点全都干掉,剩下的互相了断,假设所选出的线段共有 \(x\) 条,有个平凡的解是干掉 \(x-1\) 个端点,换句话说只有最开始的线段是两个端点都无法染色,其余的线段都可以被干掉一个端点。
你再仔细想想非平凡的情况都能归到平凡的情况里去,因为这里暗含着一个限制是所选出的线段必须覆盖整个连通块对应的区间。为什么?如果说把这个连通块分裂成两个块分别做,假设分别选出了集合 \(A,B\),那我加一条横跨两个集合的线段进去一定不劣,因为这两个块之间一定有间隙,我加入这条线段后会至少收获 \(1\) 的收益,而有一个平凡的解是 \(x-1\) 保证了我增加的代价不会超过 \(1\)。而平凡的情况中会有一个两端点都不染色的线段,这个是没法避免的,因为你最后总要拿一条线段去把别的线段端点干掉。所以非平凡的情况只能是把一些线段的两个端点都干掉了,也就是在保证其余线段能覆盖整个区间的前提下去掉某些线段。那这问题是啥?选最少的线段覆盖整个区间!直接贪心,end。
D
好像切了?尽管总思考时间加起来有一个多小时
先考虑不相交地拼接所有可能的操作区间,这相当于把区间长度加上或减去 \(b_i\)。令 \(k=\gcd b_i\) 由裴蜀定理,最终表出的区间长度一定是 \(k\) 的倍数,那么其实只需要保留一个 \(k\) 就能表出所有区间了。
现在的问题是处理相交的区间,你发现如果区间长这样相当于把两个相隔 \(k\) 的位置 \((i,i+k)\) 都取反。
而如果错开得更多一点,比如这样是把 \((i,i+1,i+k,i+k+1)\) 这四个位置都取反了,而这个也可以看做是分别把 \((i,i+k),(i+1,i+k+1)\) 取反,其余情况同理。因此相交的区间都可以归纳为把相隔 \(k\) 的两个位置 \((i,i+k)\) 上的数取反。
按 \(k\) 建立同余系,把原序列抽离为 \(k\) 个子序列。每个子序列直接是相互独立的,而且同一子序列的两个负号可以抵消,因此最终答案只与子序列上负号数量的奇偶性有关!由于每次区间操作是把连续的 \(k\) 个元素一起取反,所以它正好会把所有子序列的奇偶性改变,于是可能的情况只有两种,分别计算取 max 即可。
CF1633 edu(#122)
ABCD 都挺简单(D 题想不开吃了发 RE 的罚时亏大了),E 题想麻烦了,但 tyy 说我的思路还算正常?
可能 edu 的风格就是偏简单,但我还是很……弱智
A
一开始没转过弯来,实际上只需要改动个位数就一定能被 \(7\) 整除
B
答案一定在 \([1,n],[2,n],[1,n-1]\) 这三个区间内取得
C
\(k\) 这么小就是用来耍猴的…注意直接乘可能爆 ll,得用两个 Ceil 相比较才稳健
D
它这个题面相当于把 \(01\) 背包糊你脸上了,你需要担心的只有复杂度。不过 \(x\to x+\lfloor\frac{x}{i}\rfloor\) 这个东西增长得很快,大致是 \(\log\) 级别,然后你打个表发现最大的确实只有 \(12\)……硬跑 \(01\) 背包,做完了
E
其实很无聊的一道题……
kruskal 只关心边权的相对顺序,所以,所以考虑按 \(x\) 扫描线,什么时候边权的相对顺序会发生变化呢?位于 \(x\) 同侧的边相对顺序是固定的,只有可能是 \(w_i-x\) 和 \(x-w_j\) 这两条边的相对顺序发生改变。换句话说这个交界点一定是某两条边权的平均值,即 \(\frac{w_i+w_j}{2}\)。这个只有 \(O(m^2)\) 种,所以 MST 最多只有 \(O(m^2)\) 种。换句话说把所有交界点求出来排个序会形成若干个区间,位于同一个区间的询问的 MST 是唯一的。
赛时把绝对值的式子按照大小关系拆开了,所以想的是如果两个询问所在的边权区间相同且它们在生成树上的 rank 相同对应的 MST 就是相同的。但这东西多了个 rank 就很难做,我只会 wqs 二分,tyy 好像给了个更好的做法?
CF1638 div2(#771)
上 M 了,这是好的。
A
boring
B
exciting
奇数不可能越过奇数,偶数不可能越过偶数,其余情况为所欲为。
冒泡排序证明正确性。当奇数子序列和偶数子序列分别递增时,冒泡排序不会交换两个奇偶性相同的。
C
lucky
https://www.luogu.com.cn/problem/P4728这题优化的一部分
D
好像直接 bfs 就赢了?我也不知道为什么。
值得反思,越靠后涂的格子约束更少,因为在此之前你可以把它的四个格子任意涂色来调整其他格子的颜色,这就证明了 bfs 的正确性。
E
颜色段均摊。
CF1635 div2(#772)
赛后补题
D
好题。每个数的贡献是斐波那契数列前缀和,问题在于去重。枚举 append 了多少位,然后扫一下判断是否合法。\(O(n\log^2V)\)。
E
无趣。二分图染色然后拓扑排序
F
好题。据 tyy 说很套路?
区间子区间最值的一个思考角度是尽量减少可能产生贡献的区间,考虑 \((i,j),i<j\) 能否贡献到任意一个区间的答案里。如果 \((i,j)\) 中间有一个位置的 \(w\) 比 \(i\) 小或者比 \(j\) 小都寄了。这样的 \((i,j)\) 怎么求?考虑从左到右维护一个递增的单调栈,压入 \(i\) 时弹出的所有点 \(x\) 都满足 \(w_x\ge w_i\),而且 \((x,i)\) 里面所有数的值都大于 \(w_x\)(不然它在 \(i\) 之前就被弹出了),显然这是满足条件的。但这样的话只求出了所有 \(w_i>w_j\) 的\((i,j)\),\(w_i<w_j\) 的那些呢?再倒着扫一遍!这样就把有意义的区间数量降至了 \(O(n)\)。查询时,由于是区间子区间,所以实际上是一个被对角线截断出的 2-side 矩形查询,甚至可以使用树状数组维护 min。复杂度 \(O(n\log n)\)
CF1644 div2(Edu123)
FTL 上紫了/bx
E
如果想要到达某个点显然只需要在相邻的两个连续段里插入。那么这是 \(n\) 个矩形的面积并。
扫描线?不。由于这 \(n\) 个矩形是首尾相接的,所以你只需要沿着这些矩形的下边框和上边框走就能求出面积并。实际意义是贪心,每次能往下走就往下走,和每次能往右走就往右走可以勾勒出整个矩形并的轮廓。
F
不会/kk
CF1641 div1(#773)
这场过于刺激/jy
教训:一定要冷静。专心致志享受比赛,不要管别人的表现。
A
把 \(i\) 与 \(ix\) 贪心匹配,不足则补齐。
B
如果有一个数出现次数为奇显然不行,否则我们大胆猜想它一定有解。
利用所有数都出现了偶数次的性质,我们找到第一个数之后第一个与它相同的位置 \(i\),把 \([2,i-1]\) 这里面的值以嵌套的形式不断插入到 \(i\) 之后。如 \(1231\) 就会变成 \(12312332\),这样之后你发现 \(a[1,i-1]=a[i,2i-1]\),去掉这一段之后变成了一个规模更小的子问题,而且奇偶性没有发生改变。由此归纳得证。
C
做法一
赛时做法,能推断出 \(a_i\) 为 \(1\) 当且仅当存在一个已知和 \(>0\) 的区间经过了 \(i\) 且这段区间里其他位置都已确定为 \(0\)。
对每个位置 \(i\) 用并查集维护它左边第一个未被确定为 \(0\) 的位置 \(l\),右边第一个未被确定为 \(0\) 的位置 \(r\),把和 \(>0\) 的区间看做一条线段,问题变为是否存在一条左端点位于 \([l,i]\),右端点位于 \([i,r]\) 的线段。 直接使用线段树套 set 维护,时间复杂度为 \(O(n\log^2 n)\)。
做法二
by maruize,太强了
离线,记 \(t_i\) 表示 \(i\) 这个位置最早什么时候被确定为 \(0\)。那如果有一个信息是区间 \([l,r]\) 之和大于 \(0\),它内部能确定为 \(0\) 的点少于 \(r-l\) 个那这个信息完全没有利用价值。否则我们把未确定的点视作 \(+\infty\) 用 st 表维护最大值以及最大值的出现位置,这样可以简单地判断出 \([l,r]\) 是否只有一个最大值以及这个最大值是否为 \(+\infty\),然后把这个 \(+\infty\) 对应位置的答案设为 \(\max\),表示它在时刻 \(\max\) 之后能确定为 \(1\)。时间复杂度 \(O(n\log n)\)。
做法三(咕
by tyy
CF1648 div1
ABC 三道水题,D 过于高超
CF1654 div1+2
降大智,下大分/kx
C
其实比我想的简单的多……
首先和一定,也就是初始蛋糕的大小固定。
然后切,切出来的每一块都必须得到利用。不然的话会造成质量流失。
那么就砍 \(n-1\) 刀,递归处理。
主要是对于这种和的约束完全不敏感…全都是靠别人提示才意识到问题所在
CF1699 div2
B
这种题是不是先有的构造方式再有的约束条件啊?枚举了二十分钟构造方式才搞出来,我就完全没有灵感。
正确打开方式是把每个 2x2 的小方阵看做一个格子然后交替染成 0110 或 1001
C
如果整个序列没有 0,那么对整个序列做一次就够了。否则需要做两次。这给出了答案的上界:\(2\)
还有些特例是 0 集中在一边,特判一下就好了。
D
我被这题克制的死死的
E
感觉这题比 D 要顺畅的多啊?
CF1702 div3
毫无营养
CF1704 div1+2
手速不行,但还好。最后五分钟压哨绝杀了 E
A
略
B
略
C
我感觉这个 C 比 D 困难啊?这东西类似于插板保护连续段,显然我们不得不让某些不幸的连续段自生自灭,那么让比较短的那些段自生自灭肯定是更优的,因为一个段自生自灭后它就不会再污染别的位置了。考虑直接枚举 \(i\) 算前 \(i\) 短的段都毁灭了,其余的正常插板保护。如果说第 \(j\) 个段的长度为 \(l_j\),第一个板在 \(x\) 时刻插入,第二个板在 \(y\) 时刻插入,那它没被侵蚀的位置有 \(l_j-2x-(y-x)=l_j-x-y\)个,此时总的没被侵蚀的位置数为 \(\sum_{j\ge i}l_i-x-y\),设总共插入了 \(t\) 块板,则 \(x,y\) 恰好取遍 \([0,t)\) ,那么没被侵蚀的位置数即为 \(\sum_{j\ge i}l_i-\frac{t(t-1)}{2}\)。
CF1713 div2
E
感觉偏水。注意到一次行列互换实际上是把一些位置按对角线对称地交换了,那么这东西就像异或一样具有交换律,结合律。
然后直接贪心,拿并查集维护行的连通块及颜色。
F
太高超了 2F。首先不难发现 a 对 b 的贡献是一个杨辉三角的形式,顺着这个思路往下做会出现 补集 的 子集,然后就不太好做了。
考虑一个牛逼想法,我们先把 \(a\) 贡献到对角线上,再由对角线贡献到 \(b\)。为了方便,把 \(a\) 和对角线从右往左重编号为 \(0,1,\cdots,n-1\),那么 \(a\) 的第 \(i\) 个位置会对对角线上的第 \(j\) 个位置贡献 \(\binom{i}{j}\) 次。而我们知道 \(\binom{i}{j} \bmod 2=1\) 当且仅当 \(i,j\) 二进制分解后 \(j\) 是 \(i\) 的子集,所以由 \(a\) 求对角线只需要对 \(a\) 求超集和。同理可得由对角线推 \(b\) 只需要对对角线求子集和。这样的好处在于,没有补集了。\(i\to j\) 的贡献要么是 \(\binom{i}{j}\) 要么是 \(\binom{j}{i}\),即子集或超集。具体地,由 \(a\) 到对角线是超集和,由对角线到 \(b\) 是子集和。现在知道 \(b\),做一次子集和的逆再做一次超集和的逆就解决了/jy。非常震撼,tyy 实在是不平凡的!
CF1746 global
vp,压哨绝杀了 F。但是 BCF 我的做法好像和官方题解都不太一样啊?
A
略
B
卡了我半小时。
做法一(官方解法)
考虑最后得到的数组 \(a'\ 01\) 分界线在哪里,如果 \(a'[1,i)=0,a'[i,n]=1\) 那么需要改动 \(a[i,n]\) 中所有为 \(0\) 的位置和 \([1,i)\) 中所有为 \(1\) 的位置。假设它们分别有 \(x,y\) 个,则可断言将 \(a\to a'\) 需要且仅需要 \(\max(x,y)\) 次操作。首先一次操作最多把 \(x,y\) 分别减一,因此操作数的下界是 \(\max(x,y)\)。其次如果 \(\min(x,y)>1\) 那么总可以选一个 \([1,i)\) 中的 \(1\) 加到 \([i,n]\) 中的一个 \(0\) 上,这会使 \(x,y\) 同时减一。而如果 \(x\) 变为 \(0\) 可以不停地把后面的 \(0\) 删掉使 \(y\) 减一(对 \(0\) 操作相当于删掉 \(0\))。如果 \(y\) 变为 \(0\) 可以不停地把前面的 \(1\) 加到最后一个元素上,所以总共需要 \(\max(x,y)\) 次操作就能搞定。分析出这个之后就枚举分界线算一算。
做法二(赛时做法)
首先对 \(0\) 操作等价于把 \(0\) 删掉,对 \(1\) 操作呢?可以证明 \(1\) 只在加到 \(0\) 上时才有意义,此时操作等价于挪动一个 \(1\) 覆盖某个 \(0\)。具体地,按照 \(0,1\) 连续段的视角去看,所有操作一定是不断地把一个 \(1\) 的连续段搬到后面,覆盖某个 \(1\) 连续段前的 \(0\) 连续段。那么如果一个连续段后面的尚未被覆盖的 \(0\) 的数量大于等于当前 \(1\) 连续段的长度就直接把 \(1\) 全都搬过去就行。否则会有一部分留在原地,其余的 \(1\) 过去填,这样会使一段后缀全都连通(全都被 \(1\) 覆盖)。
综上可以看出 \(1\) 只会加到位于她后面的 \(0\) 上,对每个 \(1\) 记 \(b_i\) 表示它和哪个 \(0\) 配对了,若 \(1\) 没有和某个 \(0\) 配对那么 \(b_i=\infty\)。记 \(x=\min b_i\),那么 \([x,n]\) 这段中的 \(0\) 的数量即为答案,同时需要满足 \([x,n]\) 这段的 \(0\) 的数量大于等于 \([1,x)\) 的 \(1\) 的数量。等等……这是不是有点熟悉?没错,这个做法和官方题解实际上是等价的,只不过官方题解中没有对 \(x,y\) 的大小关系细分,而此做法实际上指出了 \(x>y\) 的情况都可以归到 \(x\le y\) 的情况,即如果我们需要让某些 \(1\) 加到最后一个元素上,那么我们把分界线向前延伸一下,如果有 \(0\) 的话那么这个 \(1\) 就可以加到这个 \(0\) 上,如果 \(0\) 的数量不够(在处理完遗留的 \(1\) 前又遇到了一些 \(1\))就是整个后缀全都连通的情况。手模一下可能有助于理解。
C
赛时做法
盲猜一手最终的逆序对数一定为 \(0\)。
差分,问题变为第 \(i\) 次操作可以给差分数组的某个元素加 \(i\),问能否在 \(n\) 次操作内把差分数组中的所有元素变为非负。贪心,在差分数组中选最小的位置加 \(n\),选次小的位置加 \(n-1\)……以此类推。你发现最坏的情况是 \(n,1,n-1,2,\cdots\),但这样也卡不掉。交上去过了,复杂度 \(O(n\log n)\)
官方做法
实在是不平凡的!
注意到差分数组 \(b_i=a_i-a_{i-1}\ge -a_{i-1}\),那么在第 \(a_{i-1}\) 次操作给 \(b_i\) 加上 \(a_{i-1}\) 即可。复杂度线性。
D
直接 dp。
E
注意到相邻的两次询问 \(S,T\) 等价于给出了 \(x\in (S\cup T),x\in (\overline{S}\cup T),x\in (S\cup \overline{T}),x\in (\overline{S}\cup \overline{T})\) 这四种限制中的一种。第一个想法是尽量保证每次询问的集合大小恰为一半。
E1
分两次询问分一组,然后直接搞,每次可以把 \(n\to \frac{3}{4}n\) 。n=3 的时候有点细节,你需要用一个很耍赖的办法”骗“出交互库的真话。首先问两次相同的询问(只问一个数),如果有 YES 就 answer 这个数,如果蒙对了就赢,否则说明交互库的这次回答是假话,那么接下来的回答一定是真话,在剩下的两个数中随便选一个问。如果全都是 NO,由于两次询问不可能全为假话,因此这两次询问一定都是真话,也就能排除掉这个数,进入 \(n=2\) 的情形。
E2
蚍蜉撼树,试图干掉 *3200,最终被教育了QAQ。
每两次询问分一组还是太憨憨了,浪费了非常多的信息。考虑每 \(x\) 次询问分一组,首先还是要保证每次询问的集合大小尽可能接近一半,这让我们联想到二进制。根据二进制表示的第 \(i\) 位决定它是否选入第 \(i\) 次询问的集合里。然后会得到 \(x-1\) 条限制,每条限制 ban 掉了第 \(i\) 位与第 \(i+1\) 位的四种可能取值中的一种。然后你写个 dp 推一推发现如果 \(n\) 为 \(2\) 的整次幂那么留下来的数的数量恰为斐波那契数 \(f_{x+2}\)(\(f_1=f_2=1\))。那么理想状态下每次会让 \(n\to \frac{f_{x+2}}{2^x}\),写个程序算一算次数恰好够用。
然而理想很丰满,现实很骨感。事实是在 \(n\not= 2^k\) 时我们根本无法构造出一种均匀的划分。我最开始的想法是 随机化,本地测问题不大,但是被实际评测用的动态交互库卡飞了。最坏是 \(68\) 次左右。正确的打开方式是 dp,dp 最优的划分方案。其实我在刚开始卡次数的时候也想到过,只是 dp 只有指数级别的做法,经 1789 提示好像还要优化这个 dp。这么说这个题也太恐怖了,不愧是 *3200,走为上策!!!
F
这种东西如果你尝试去想正经做法会发现它本质困难,一个例证是它涉及到的维度多达 \(O(n)\) 而且不同维度间没有显式联系。那么考虑一些不正经的做法,比如随机化。将所有维度利用随机化压成一个维度。
随机化的角度是由结论推性质,如果所有数都出现了 \(k\) 的整数倍次能推出什么呢?一个自然的想法是所有数的出现次数之和应当是 \(k\) 的整数倍,但这样显然会被卡飞。接下来就是随机化的用武之地。
官方做法
记 \(A\) 为所有出现过的值的集合,从 \(A\) 中随一个子集 \(S\) 出来,只保留这些值,其余视为 \(0\)。对于一次查询 \(l,r,k\),如果 \(l,r\) 中 \(1\) 的数量不是 \(k\) 的整数倍那么这次查询的答案一定为 NO,否则视为 YES。这样做的正确概率是多少呢?记 \(c_i\) 表示原本区间中 \(i\) 出现次数模 \(k\) 的结果,\(c_i=0\) 它对准确率无影响。那么相当于有一个元素均在 \([1,k)\) 之间的可重集 \(S\),问从 \(S\) 里随一个子集出来子集和为 \(0\) 的概率。先选定一个特殊的元素 \(x\),建立子集与子集之间的双射 \(T \xleftrightarrow{\operatorname{xor} x} T'\)。即包含 \(x\) 和去掉 \(x\),由于 \(x\not= 0\),这两者中至少有一个的子集和不为 \(0\)。所以随出子集和为 \(0\) 的概率 \(\le \frac{1}{2}\),即错误率 \(\le \frac{1}{2}\)。那么这样做 \(30\) 次就赢了。
怎么随一个子集?每个元素有 \(\frac{1}{2}\) 的概率被选进去。这里看起来需要每次都生成一个 \([0,1]\) 之间的随机数,常数还是有点大的,有一个小 trick (感谢 tourist 的代码)是可以用一个 unsigned int 范围内的随机数代表这 \(30\) 次随机的结果,类似状压。
赛时做法
很奇怪。还是记 \(c_i\) 为出现次数,有一个想法是记和,记差,但这样还不够。考虑如果 \(\forall i,c_i\equiv0\pmod k\to \sum c_is_i\equiv 0\pmod k\)。那么可以随机 \(s\) 序列,问题转为单点修改区间求和。单次错误率不会分析,反正做 22~25 次就赢了。不过这东西常数很大,是擦着边冲过去的。

 会及时更新哒,也欢迎来催更~
会及时更新哒,也欢迎来催更~

 浙公网安备 33010602011771号
浙公网安备 33010602011771号