【2019】A Game-Theoretic Approach to Computation Offloading in Satellite Edge Computing

A Game-Theoretic Approach to Computation Offloading in Satellite Edge Computing

文献类型	文献年份	文献来源
期刊	2019年	IEEE Access

标题

基于博弈论的计算分流算法

关键词

• 博弈论
• 卫星边缘计算
• 计算分流

abstract

考虑了卫星绕行引起的间歇性地面卫星通信。 我们进行了一个计算卸载游戏框架，并根据排队论作为优化性能的指标，计算了任务的响应时间和能耗。 从理论上证明了纳什均衡的存在性和唯一性，并提出了一种迭代算法来找到纳什均衡。 仿真结果验证了该算法的有效性，并表明基于游戏的卸载策略可以大大降低设备的平均成本。

• 考虑到卫星引起的间歇性通信，只有在窗口期才能够进行通信
• 假设一个卫星上只部署一个MEC服务器
• 基于排队论
• KPI：响应时延与能耗

模型

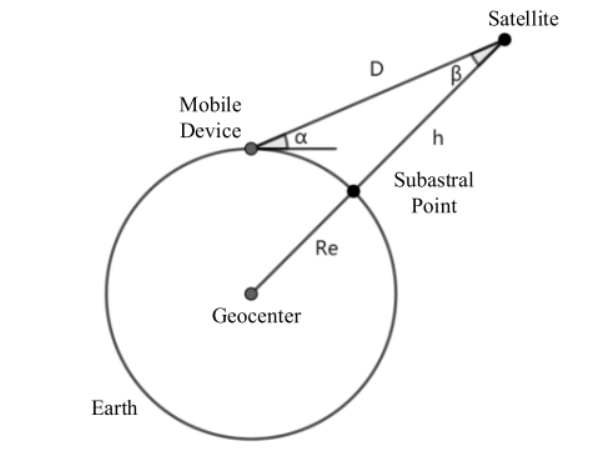
1-卫星的轨道模型

\[\alpha=\arctan \frac{\cos \Delta \phi \cos \varphi_{t} \cos \varphi_{s}+\sin \varphi_{t} \sin \varphi_{s}-\frac{R_{e}}{R_{e}+h}}{\sqrt{1-\left(\sin \varphi_{t} \sin \varphi_{s}+\cos \Delta \phi \cos \varphi_{t} \cos \varphi_{s}\right)^{2}}} \]

变量	含义
\(\phi_{t}\)	设备的经度
\(\varphi_ {t}\)	设备的维度
\(\phi_{s}\)	卫星的经度
\(\varphi_ {s}\)	卫星的维度
\(\Delta\phi =\phi_ {t}-\phi_ {s}\)	设备与卫星的经度差
\(R_{e}\)	地球半径
\(h\)	卫星距离地面高度

只有当\(\alpha>0\)才能进行数据的传输，并且我们假设地面的设备距离很近，他们在一个固定的很小的区域内，因此它们与卫星的几何关系相同

根据仰角\(\alpha\)的正负，正就是可以通信，负无法通信，我们定义一个（轨道）周期内的通信时间

\[\theta = \{\theta_{1}, \theta_{2},...\theta_{M} \} \\ 0\le\theta_{j}\le1 \]

\(\theta_{j}\)表示设备在轨道周期内可以与卫星J通信的时间的百分比。

2-通信模型

注意：

1. 只考虑上载，返回结果这一部分忽略，（这是因为结果数据远远小于输入数据）
2. 考虑到移动设备间的干扰

移动设备i任务到卫星j的上行链路数据速率\(R_{i,j}\)

\[R_{i, j}=B \log _{2}\left(1+\frac{p_{i} g_{i, j}}{\sigma_{0}+\sum_{s \in \mathbf{N}, s \neq i} p_{s} g_{s, j}}\right) \]

B表示信道带宽，pi表示设备i的发射功率，\(g_{i,j}\)表示设备i与卫星j之间的信道增益，σ0表示背景噪声功率

根据上载数据链路\(R_{i,j}\)的公式可以得到

• 任务的传输速率\(R_{i,j}\)与设备的发射功率\(P_{i}\)成正相关
• 过高的发射功率\(P_{i}\)会导致过多的能量消耗
• 过多设备的卸载，将导致速率降低

3-计算模型

假设每个移动设备可以生成一系列同类任务。 设备i生成的任务可以用所需的资源和数据大小来表示，即Taski = {ci，di}

• 其中ci表示执行任务所需的计算资源数量； 例如，可以通过CPU周期数来量化ci
• di表示描述任务的某些信息（例如程序代码或相应数据）的计算输入文件的大小
• \(C_{i}^{(m)}\)和\(C_{j}^{(s)}\)是设备和卫星的计算能力，用一秒CPU周期数表示

地面设备和卫星可以看作是个排队的M/G/1模型

• 任务的生成是指数分布，任务的执行是随机分布
• 每个任务的生成是独立同分布的iid，
• 任务以\(\lambda_{i}\)生成，指数分布的均值就是\(1/\lambda_{i}\)

设备i在本地执行并和分流到卫星的任务的百分比定义为设备i的计算分流策略

\[\mathbf{x}_{i}=\left\{x_{i, 0}, x_{i, 1}\right....x_{i,M}\} \]

\(x_{i,0}\)表示本地执行的任务的百分比,\(x_{i,j}\)表示分配给卫星\(j\)的百分比

满足一下约束条件

\[\begin{aligned} x_{i, j} \geq 0, & \forall i \in \mathbf{N}, \forall j \in \mathbf{M} \\ \sum_{j=0}^{M} x_{i, j}=1, & \forall i \in \mathbf{N} \end{aligned} \]

表示1.百分比只可能为正数或者是0（表示不往该设备卸载）2.所用的相加要等于1，3.隐含的每个要小于1

博弈论模型

The strategy of player i is the percentage of tasks that are executed locally on a device or offloaded to satellite, denoted by xi =
xi,0, xi,1, . . . , xi,M ∈ Xi, as described in Section III.
Here, Xi, which is the set of strategies ofdevice i, is closed and
convex (because ofXi ⊆ RM and xi,0+ xi,1+ . . .+ xi,M = 1).

• 这里的\(X_{i}\)就是设备i的策略集，令\(X=X_{1}*X_{2}*...X_{N}\)是所有设备策略组合的集合

• 所有设备的整体策略我们可以用\(\mathbf{x}=\left\{\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{N}\right\} \in X\)表示中间的\(\mathbf{x_{i}}\)表示设备i的策略

• \(\mathbf{x_{-i}}=\left\{\mathbf{x}_{1},... \mathbf{x}_{i-1}, \mathbf{x}_{i+1}\ldots, \mathbf{x}_{N}\right\} \in X\)表示除玩家\(i\)以外的所有玩家策略的向量

KPI指标（性能指标）选择平均响应时延与平均功耗，玩家\(i\)（设备）的成本函数

\[P_{i}\left(\mathbf{x}_{i}, \mathbf{x}_{-i}\right)=T_{i}+\mu_{i} E_{i} \]

这是一个典型的博弈论问题。 要优化的目标函数不仅与其策略有关，而且与其他参与者的策略有关。

指标计算

分流到卫星

如果移动设备i将任务卸载到卫星j，则需要执行三个步骤：

• 卸载任务，
• 在卫星上执行，
• 然后返回结果

由于卫星的高动态性，设备i不能总是与卫星j通信。 因此，在卸载和返回时都应考虑通信的等待时间

1. 卸载的平均响应时间

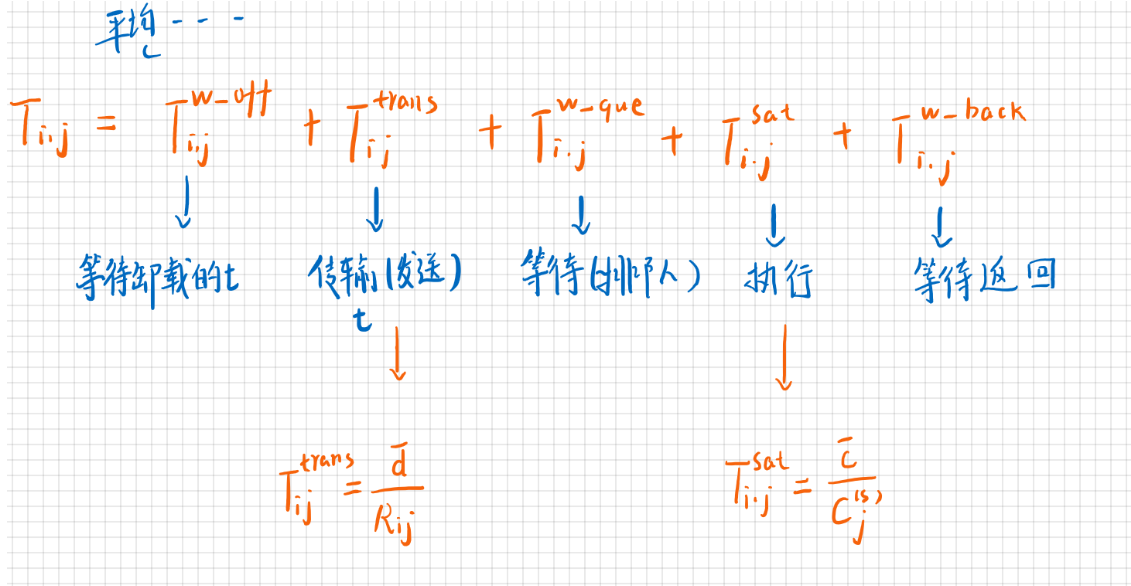
\(T_{j} \gg T_{i, j}^{s a t}+T_{i, j}^{w_{-} q u e}\) \(T_{j}\)是卫星j的轨道周期

根据排队理论[34]，卫星j上任务的平均排队等待时间为 （M/G/1）

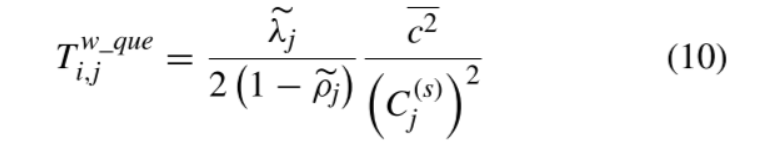
总式子

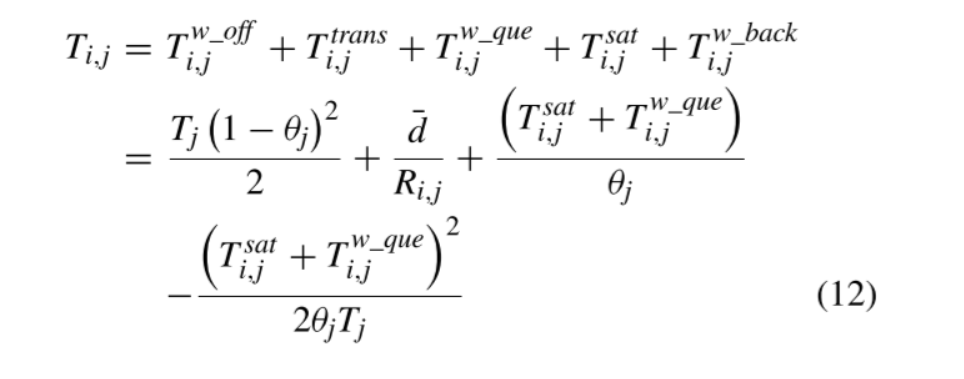
2. 能耗

传输能耗、执行能耗

执行能耗与CPU频率的平方成正比

传输能耗

\[E_{i, j}^{\text {trans}}=p_{i} T_{i, j}^{\text {trans}}=\frac{p_{i} \bar{d}}{R_{i, j}} \]

执行能耗

\[E_{i, j}^{s a t}=\kappa\left(C_{j}^{(s)}\right)^{2} \bar{c} \]

其中κ是取决于芯片架构的有效开关电容

总式子

\[E_{i, j}=E_{i, j}^{t r a n s}+E_{i, j}^{s a t}=\frac{p_{i} \bar{d}}{R_{i, j}}+\kappa\left(C_{j}^{(s)}\right)^{2} \bar{c} \]

分流到本地执行

1. 时延

   排队时延+执行时延 （对比少了，传输，卫星上排队时间，等待返回，）

   \[T_{i, 0}=T_{i, 0}^{w_{-} q u e}+T_{i, 0}^{l o c} \]

   执行时延

   \[T_{i, 0}^{l o c}=\frac{\bar{c}}{C_{i}^{(m)}} \]

   本地排队时延

   \[T_{i, 0}^{w a i t}=\frac{\lambda_{i}}{2\left(1-\rho_{i}\right)} \frac{\overline{c^{2}}}{\left(C_{i}^{(m)}\right)^{2}}=\frac{x_{i, 0} \lambda_{i} \overline{c^{2}}}{2\left(C_{i}^{(m)}-x_{i, 0} \lambda_{i} \bar{c}\right) C_{i}^{(m)}} \]

   总式子

   \[T_{i, 0}=T_{i, 0}^{w_{-} q u e}+T_{i, 0}^{l o c}=\frac{x_{i, 0} \lambda_{i} \overline{c^{2}}}{2\left(C_{i}^{(m)}-x_{i, 0} \lambda_{i} \bar{c}\right) C_{i}^{(m)}}+\frac{\bar{c}}{C_{i}^{(m)}} \]

2. 能耗

   \[E_{i, 0}=\kappa\left(C_{i}^{(m)}\right)^{2} \bar{c} \]

总式子

1. 时延

   \[T_{i}=x_{i, 0}\left(T_{i, 0}^{w a i t}+T_{i, 0}^{l o c}\right)+\sum_{j=1}^{M} x_{i, j} T_{i, j} \]

2. 能耗

   \[E_{i}=x_{i, 0} E_{i, 0}+\sum_{j=1}^{M} x_{i, j} E_{i, j} \]

纳什均衡的证明与唯一性

两个引理：

Lemma 1: At least one Nash equilibrium for a non-cooperative game G = {x1, x2, . . . , xN; P1, P2, . . . , PN}
is existence if, for all 1 ≤ i ≤ N:

(1) The strategy space Xi is a non-empty, convex, and compact subset of some Euclidean space.

(2) The cost function Pi (xi, x−i) is continues and
quasi-convex in Xi.

非合作博弈，至少有一个Nash均衡：

• 条件1 ：策略空间Xi是某些欧几里得空间的非空，凸且紧致子集

• 条件2：成本函数Pi（xi，x−i）连续且在Xi中为准凸

第一个引理，证明至少有一个Nash均衡

Lemma 2: A continuous and twice differentiable function P(x), where x = (x1, x2, . . . , xM), is convex if and only if its Hessian matrix of second partial derivatives is positive semidefinite.

\[\mathbf{H}(P(\mathbf{x}))=\left[\frac{\partial^{2} P}{\partial x_{i} \partial x_{j}}\right]_{M \times M} \]

有点难,没看懂

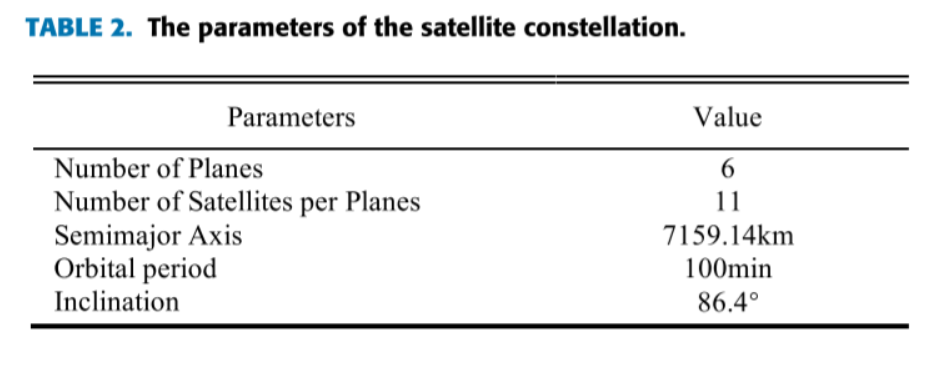
仿真参数

轨道选择是铱星

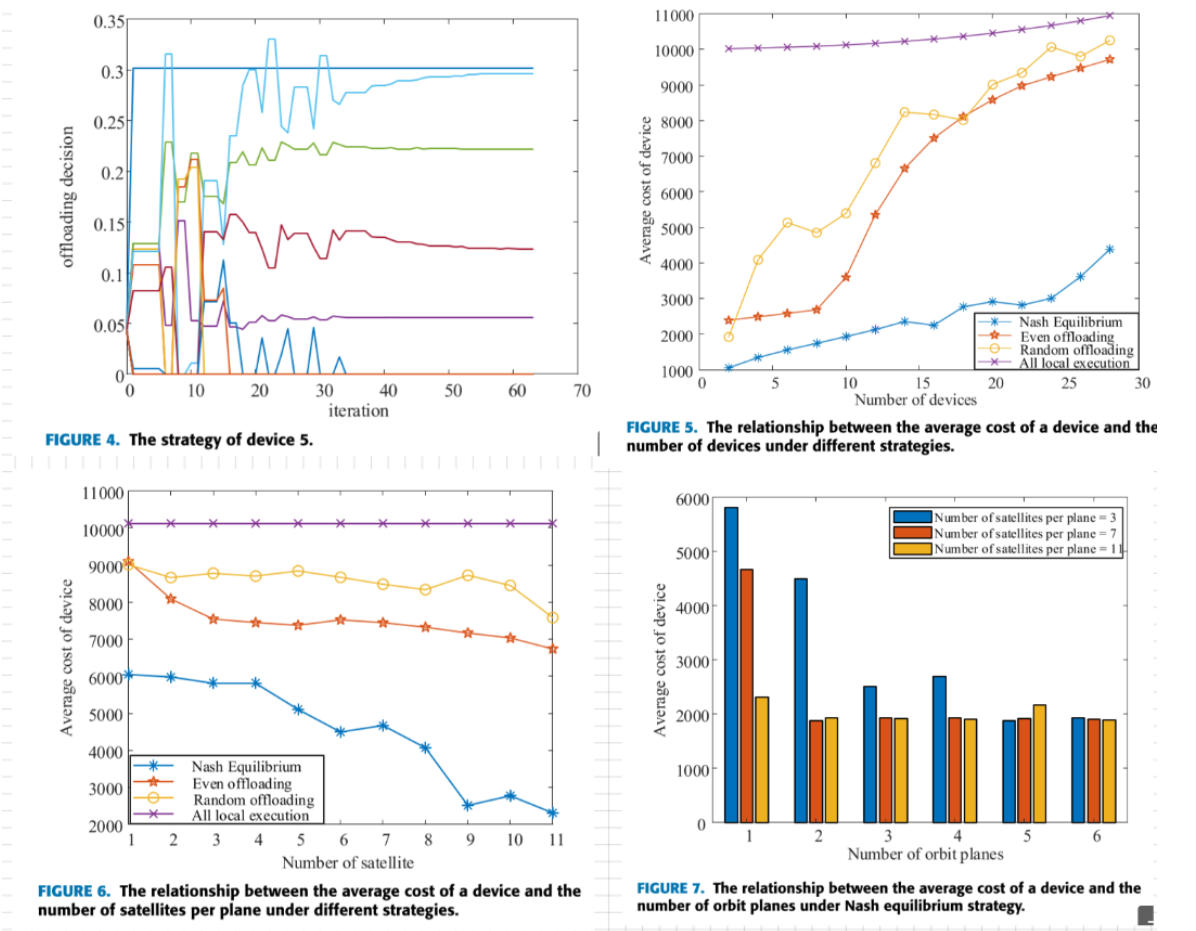
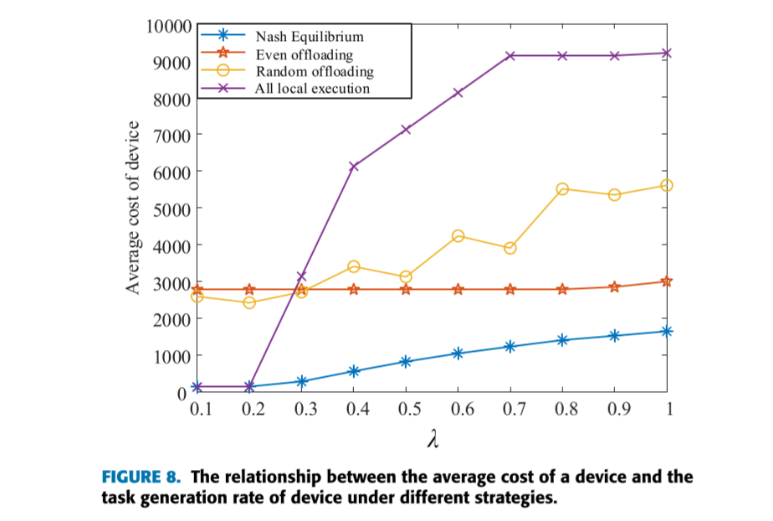
结论