OI中字符串相关算法/数据结构总结
定义 oi-wiki
字符集
一个 字符集 \(\Sigma\) 是一个建立了 全序 关系的集合,也就是说,\(\Sigma\) 中的任意两个不同的元素 \(\alpha\) 和 \(\beta\) 都可以比较大小,要么 \(\alpha<\beta\),要么 \(\beta<\alpha\)。字符集 \(\Sigma\) 中的元素称为字符。
字符串
一个 字符串 \(S\) 是将 \(n\) 个字符顺次排列形成的序列,\(n\) 称为 \(S\) 的长度,表示为 \(|S|\)。
如果字符串下标从 \(1\) 开始计算,\(S\) 的第 \(i\) 个字符表示为 \(S[i]\);
如果字符串下标从 \(0\) 开始计算,S 的第 \(i\) 个字符表示为 \(S[i-1]\)。
子串
字符串 \(S\) 的 子串 ,\(S[i..j]\),\(i≤j\),表示 \(S\) 串中从 \(i\) 到 \(j\) 这一段,也就是顺次排列 \(S[i],S[i+1],\ldots,S[j]\) 形成的字符串。
有时也会用 \(S[i..j]\),\(i>j\) 来表示空串。
子序列
字符串 \(S\) 的 子序列 是从 \(S\) 中将若干元素提取出来并不改变相对位置形成的序列,即 \(S[p_1],S[p_2],\ldots,S[p_k],1\le p_1< p_2<\cdots< p_k\le|S|\)。
后缀
后缀 是指从某个位置 i 开始到整个串末尾结束的一个特殊子串。字符串 S 的从 i 开头的后缀表示为 \(\textit{Suffix(S,i)}\),也就是 \(\textit{Suffix(S,i)}=S[i..|S|-1]\)。
真后缀 指除了 \(S\) 本身的 \(S\) 的后缀。
前缀
前缀 是指从串首开始到某个位置 \(i\) 结束的一个特殊子串。字符串 \(S\) 的以 \(i\) 结尾的前缀表示为 \(\textit{Prefix(S,i)}\),也就是 \(\textit{Prefix(S,i)}=S[0..i]\)。
真前缀 指除了 \(S\) 本身的 \(S\) 的前缀。
字典序
以第 \(i\) 个字符作为第 \(i\) 关键字进行大小比较,空字符小于字符集内任何字符(即:\(a< aa\))。
回文串
回文串 是正着写和倒着写相同的字符串,即满足 \(\forall 1\le i\le|s|, s[i]=s[|s|+1-i]\) 的 \(s\)。
KMP
算法
本质思想:利用已知前缀函数递推。
前缀函数
定义 \(\pi(i)\) 表示字符串 \(s\) 最长的真前缀的长度 \(len\),满足 \(s[1 \ldots len] = s[i-len+1 \ldots i]\)。这一段前缀称为 \(s\) 的 \(\text{Border}\)。
文本串与模式串的匹配
加入我们已经求出了 \(p\) 的所有 \(\pi(i)\),考虑现在如何优化匹配的过程。
约定:使用 \(s[l \ldots r]\) 在 \(r<l\) 时表示空字符串。
使用两个指针 \(i,j\),\(i\) 指向 \(s\),\(j\) 指向 \(p\),代表考察到 \(s[1 \ldots i]\) 时的一段后缀 \(s[i-j+1 \ldots i]\) 与 \(p[1 \ldots j]\) 是匹配的。
现在枚举 \(i\) 从 \(1 \sim n\),要求最大的一个 \(j\)。由于已经求出来了 \(1 \sim i-1\) 的最大的 \(j\),考虑如何调整得到 \(i\) 的答案。
不难发现,当 \(s[i]=p[j+1]\) 时,代表继承上一次的答案仍然可以匹配,直接 \(j \gets j+1\) 即可。
否则,当 \(s[i] \not = p[j+1]\) 时,就代表 \(j\) 时不符合条件的,必须将 \(j\) 回退到一个最大的位置,使其有可能满足条件。这个最大的位置就是 \(\pi(j)\),接下来考虑证明这一点:
- \(\pi(j)\) 是可以的,因为 \(p[1 \ldots \pi(j)] = p[j -\pi(j)+1,j] = s[i-\pi(j)+1,i]\),维护了 \(i,j\) 指针的含义。
- 不能够是 \(\pi(j)\) 以前的位置,因为 \(\pi(j)\) 是可以的,这样不能保证 \(j\) 的最大性。
- 不能是 \(\pi(j)\) 以后的位置,假如 \(j_0 > \pi(j)\),仍然维护了指针的含义,那么有:\(s[i-(j-j_0+1)+1 \ldots i] = p[j_0\ldots j] = p[1,j - j_0 +1]\),发现这是 \(p\) 的 \(\text{Border}\),由于 \(j_0 > \pi(j)\) ,与 \(\pi(j)\) 的最大性矛盾!
这样就得到了文本串与模式串的匹配流程:
- 如果 \(p[j+1] \not = s[i]\),回退 \(j\) 指针直到 \(p[j+1] = s[i]\) 或 \(j=0\)。
- 如果 \(p[j+1] = s[i]\),\(j \gets j+1\)。
- 如果 \(j=m\),代表匹配成功,直接让 \(j \gets \pi(j)\) 以支持下一次匹配。
for(int i=1,j=0;i<=n;++i)
{
while(j&&s1[i]!=s2[j+1]) j=nxt[j];
if(s1[i]==s2[j+1]) ++j;
if(j==m)
{
cout<<i-m+1<<endl;//开始的匹配位置
j=nxt[j];
}
}
预处理前缀函数
特别地,有 \(\pi(0) = \pi(1) = 0\)。
沿用上面的思想,我们复制一份 \(p\),让两个指针分别指向 \(p\),含义不变,此时的 \(i\) 正好表达了一段后缀,\(j\) 表达了最大的匹配前缀,直接沿用上面的过程就结束了。
nxt[0]=nxt[1]=0;
for(int i=2,j=0;i<=m;++i)
{
while(j&&s2[j+1]!=s2[i]) j=nxt[j];
if(s2[j+1]==s2[i]) ++j;
nxt[i]=j;
}
应用
失配树
链接下文失配树。
求最小循环节
在这里先给出一些结论:
-
\(s[1 \ldots len]\) 是 \(s\) 的循环节的充要条件是 \(s[1 \ldots n -len] = s[1+len \ldots n] \wedge n \equiv 0 \pmod {len}\)。
证明:必要性显然,现在证明充分性。
由于 \(n \equiv 0 \pmod {len}\),那么字符串由 \(\frac{n}{len}\) 个字段拼接而成。
考虑在 \(s[1 \ldots n-len]\) 中每间隔 \(len\) 个字符取出字段。
可以得到 \(s[1\ldots len],s[len+1\ldots2len],\dots,s[n-2len+1,n-len]\)。
同理对于 \(s[1+len \ldots n]\) 得到:
\(s[len+1\ldots 2len],s[2len+1\ldots 3len],\dots,s[n-len+1\ldots n]\)
由相等的条件可知 \(s[1 \ldots len] = s[len+1\ldots 2len]=s[2len+1,\ldots3len]=\dots = s[n-len+1\ldots n]\)。
故 \(len\) 是原字符串的循环节!
-
\(s\) 的所有循环节一定是最小循环节的倍数。
使用反证法,假设最小循环节为 \(len_1\),存在循环节 \(len_2\) 满足 \(d=\gcd(len_1,len_2)<len_1\)。
由裴蜀定理,存在 \(x,y\) 满足 \(len_1 x+len_2 y = d\)。
由于 \(s[i]=s[i+k_1len_1]=s[i+k_2len_2]\) 都成立。
\(s[i]=s[i+k_1len_1+k_2len_2] = s[i+d]\),与 \(len_1\)是最小循环节矛盾!
故所有循环节都是最小循环节的倍数。
-
如果已知一个字符串是最小循环节至少重复两次,那么最小循环节长度就是 \(n-\pi(n)\)。
证明:假设 \(s=t^k\),\(t\) 为 \(s\) 的最小循环节, \(|t|=len\)。
由于取前后 \(k-1\) 个循环节一定是相等的,有 \(\pi(n) \ge len(k-1)\),接下来证明 \(\pi(n) = len(k-1)\)。
假设 \(\pi(n) = L=len(k-1) + r,0 \le r < len\),所以 \(s[1 \ldots r] = s[len-r+1\ldots len] \wedge s[1\ldots len-r] = s[len-r+1\ldots len]\),由性质 \(\text{2}\),取 \(d= \gcd(len,len-r)=\gcd(len,r)\),可以证明 \(d\) 是串的一个循环节,与 \(len\) 的最小性矛盾!
故 \(\pi(n) \le len(k-1)\),得到 \(\pi(n) = len(k-1)\),所以最短循环节长度就是 \(n-\pi(n)\)。
-
在 \(\text{3}\) 的基础上,如果给出的仅为原字符串的子串,结论仍然不变。
不妨记原来的字符串的前缀函数为 \(\pi'(n)\) 且下标不继承。
感性理解一下,完整周期串之前加上了周期串的后缀 \(t_1\) 那么 \(\pi(n)\) 相比原来增加了 \(|t_1|\),因为 \(s[1\ldots |t_1|] + s[|t_1|+1 \ldots |t_1|+\pi'(n)] = s[n-\pi'(n)+|t_1|-1\ldots n-\pi'(n)] + s[n-\pi'(n)+1 \ldots n]\),证明新的 \(\pi(n) = \pi'(n) + |t_1|\),由于 \(n=n'+|t_1|\),所以最短循环节长度仍为 \(n-\pi(n)\)。
在后面接上一段前缀同理,这样就证明了性质 \(\text{5}\)。
P4391 [BalticOI 2009] Radio Transmission 无线传输
性质 \(\text{4,5}\) 的运用,直接输出 \(n-\pi(n)\) 即可。
优化 DP
P7114 [NOIP2020] 字符串匹配
考虑枚举 \((AB)\) 然后统计满足条件的 \(A\),注意到应用性质 \(\text{3}\) 可以很快地算出来循环节,利用性质 \(\text{1}\) 可以很快判断是不是循环节。
只需要枚举 \((AB)\) 然后看一下 \((AB)^i\) 是否满足条件即可,时间复杂度是调和级数 \(\Theta(n \ln n)\)。
然后考虑如何满足 \(F(A)\le F(C)\) 这个条件。
先预处理出前后缀出现次数为奇数的字符数量,然后在枚举 \((AB)\) 的过程中维护出现奇数次的字符数为 \(i\) 时可行的 \(A\) 的数量即可,总复杂度 \(\Theta(n(|\Sigma|+\ln n))\)。
失配树
问题提出
在 kmp 算法中,我们已经 \(\Theta(n+m)\) 求出了前缀函数的值,那么我们想要求次大的前缀函数怎么求呢?
结论:次长的前缀函数值为 \(\pi(\pi(i))\),满足 \(s[1 \ldots \pi(\pi(i))] = s[i-\pi(\pi(i))+1 \ldots i]\)。
证明是显然的,利用 \(\pi\) 的最大性反证法即可。
那么不难发现,次次大的前缀函数就是 \(\pi(\pi(\pi(i)))\)。
这样,我们连边 \(i \to \pi(i)\) 就得到了一棵树,这就是失配树,这样向上跳 \(k\) 级得到的就是第 \(k\) 大的 \(\pi\)。
P5829 【模板】失配树
先构建出失配树,考虑询问,发现前缀 \(s[1 \ldots p]\) 的所有 \(\text{border}\) 长度构成了 \(\pi(p) \to \pi(\pi(p)) \to \ldots \to root\) 的一条路径,这样 \(p,q\) 的最长公共 \(\text{border}\) 长度就是 \(\pi(p),\pi(q)\) 的 \(\text{lca}\)。
P2375 [NOI2014] 动物园
依然是先建出失配树,倍增地往上跳直到长度小于一半。
时间复杂度 \(\Theta(Tn\log n)\)
\(\text{Trick}\):倍增数组将 \(\log n\) 开在前一维可以减少常数,友好 \(\text{Cache}\)。
exKMP / Z 函数
核心思想:依然是根据 \(z(1) \sim z(i-1)\) 的信息推出 \(z(i)\) 的答案,同时维护 \(\text{Z-box}\) 这个东西。
定义
对于一个模式串 \(s\),其 \(\text{Z}\) 函数定义为 \(z(i)\),表示最大的 \(z(i)\) 满足 \(s\) 的一段前缀等于 \(s\) 以 \(i\) 开头的后缀的前缀,即 \(s[1 \ldots z(i)] = s[i \ldots i+z(i)-1]\)。
定义 \(i\) 的 \(\text{Z-box}\) 表示区间 \([i,i+z(i)-1]\)。
exKMP 的算法流程
我们根据之前已经有的信息算出接下来的 \(z\) 值,同时维护右端点最靠右的 \(\text{Z-box}\)。
首先有 \(z(1) = m\),我们从 \(z(2)\) 开始计算,初始 \(\text{Z-box} = [l,r] = [0,0]\)。
-
假如已经算到了 \(i\),前 \(i-1\) 的 \(z(i)\) 已经被算出。
-
分情况讨论:
-
\(i \le r\):代表 \(i\) 落在当前的 \(\text{Z-box}\) 内,继续分情况讨论:
-
\(z(i-l+1) \le r-i+1\):这说明可以直接更新 \(z(i) = z(i-l+1)\)。
证明:\(p[l \ldots r] = p[1 \ldots r-l+1]\),所以 \(p[i \ldots r] = p[i-l+1 \ldots r-l+1]\)。
结合 \(z(i-l+1)\) 有:
\(p[i-l+1 \ldots i-l+1 + z(i-l+1) -1 ] = p[1 \ldots z(i-l+1)] = p[i,i+z(i-l+1)-1]\)
这样就证明了 \(z(i) = z(i-l+1)\)。
-
\(z(i-l+1) > r-i+1\):这样相比上面的情况会出现一个问题:我们的新的 \(z(i)\) 值超过了 \(\text{Z-box}\),这是,由于不知道盒子之外的字符是什么样的,我们不能笃定它们一定相等,所以就只能先将 \(z(i) \gets r-i+1\),然后暴力地扫描盒子外的字符。
-
-
\(i > r\):此时超出了 \(\text{Z-box}\) 维护的范围,直接暴力扩展即可、
-
-
得到当前的 \(z(i)\) 后,更新 \(r\) 最靠右的 \(\text{Z-box}\)。
void get_z()
{
z[1]=m;
for(int i=2,l=0,r=0;i<=m;++i)
{
if(i<=r) z[i]=min(r-i+1,z[i-l+1]);
while(i+z[i]<=m&&b[1+z[i]]==b[i+z[i]]) ++z[i];
if(i+z[i]-1>r) l=i,r=i+z[i]-1;
}
}
给定文本串的匹配
现在给定文本串 \(s\),求 \(z'(i)\) 表示最大的 \(z'(i)\) 满足 \(s\) 的一段前缀等于 \(p\) 以 \(i\) 开头的后缀的前缀。
这跟求解 \(z\) 函数的过程是类似的,在 \(s\) 上维护一段 \(\text{Z-box}\) 即可。
void get_p()
{
for(int i=1,l=0,r=0;i<=n;++i)
{
if(i<=r) p[i]=min(r-i+1,z[i-l+1]);
while(i+p[i]<=n&&b[1+p[i]]==a[i+p[i]]) ++p[i];
if(i+p[i]-1>r) l=i,r=i+p[i]-1;
}
}
应用
D. Prefixes and Suffixes
先试用 \(\text{KMP}\) 求出字符串所有公共前后缀,然后考虑怎么统计这些字符串在字符串中出现的次数。
这不难和 \(\text{Z}\) 函数关联起来,因为涉及到字符串的一段前缀和一段后缀的前缀的关系。
所有公共前后缀的长度的集合记为 \(S\),那么 \(S\) 中的元素是两两不等的。
我们枚举 \(i\) 来计算以 \(i\) 开头的所有后缀带来的贡献。
假设在 \(i\) 处的 \(\text{Z}\) 函数值为 \(z(i) \not = 0\),那么它的含义是 \(s[1 \ldots z(i)] = s[i \ldots i+z(i)-1]\),显然,它对所有 \(j \in S\) 且 \(j \le z(i)\) 能产生 \(1\) 的贡献,这样就可以在权值上差分了。(我用的权值树状数组,蠢爆了)。
Manacher
跟 \(\text{exKMP}\) 的思想有异曲同工之妙,但关注点放在了回文半径上。
\(\text{Trick}:\) 回文串有奇回文串与偶回文串之分,此时只要将每个字符中间出入一个 \(\Sigma\) 之外的特殊字符,即可将问题统一转化为奇回文串的问题。
求解过程
要求解每个位置的最长回文半径 \(d(i)\),假设前 \(i-1\) 个已经计算出来,同时维护了一段区间 \([l,r]\) 表示右端点最大的回文区间。
- 假设 \(d(1) \sim d(i-1)\) 都已经算出,现在要算 \(d(i)\)。
- 分情况讨论:
-
若 \(i \le r\),继续分情况讨论:
- 若 \(d(r-i+l) \le r-i+1\),说明 \(d(i) = d(r-i+l)\) 这是由于回文串的对称性。
- 若 \(d(r-i+l) > r-i+1\),由于不知道 \(r\) 指针右边的信息,只能 \(d(i) \gets r-i+1\) 然后暴力扩展。
-
若 \(i > r\),暴力扩展左右端点即可。
-
- 更新右端点最大的回文区间。
void manacher()
{
d[1]=1;
for(int i=2,l=0,r=1;i<=n;++i)
{
if(i<=r) d[i]=min(d[r-i+l],r-i+1);
while(i+d[i]<=n&&s[i+d[i]]==s[i-d[i]]) ++d[i];
if(i+d[i]-1>r) l=i-d[i]+1,r=i+d[i]-1;
}
rep(i,1,n) maxx=max(maxx,d[i]);
}
应用
P4287 [SHOI2011] 双倍回文
考虑求出最长回文半径后怎么做,设 \(x,y\) 分别为串的回文中心,右侧的回文串的回文中心,那么以 \(x\) 为中心的 双回文串 \(y\) 应满足 \(d(x) \ge 2(y-x) \wedge d(y) \ge y-x\) ,同时 \(d(x)\) 为偶数,\(x-y\) 为偶数。
移项,转换成对 \(y\) 的约束:
这样就可以枚举 \(x\),将满足第二个约束的 \(y\) 插入 set 中,再二分最大的 \(y\) 满足第一个约束,时间复杂度 \(\Theta(n \log n)\)。
AC 自动机
kmp 算法已经能在 \(\Theta(n+m)\) 的时间内解决单个文本串与单个模式串的匹配问题了。如果扩展问题为多个模式串,单个文本串如何快速求解。
在 \(\text{trie}\) 树上利用 \(\text{kmp}\) 的思想求出类似的 \(fail\) 数组加速跳转就是 \(\text{AC}\) 自动机的基本思想。
前置思想
回顾 \(\text{kmp}\) 算法的另一种写法。
nxt[0]=nxt[1]=0;
for(int i=2;i<=m;++i)
{
int j=nxt[i-1];
while(j&&s2[j+1]!=s2[i]) j=nxt[j];
if(s2[j+1]==s2[i]) ++j;
nxt[i]=j;
}
这代表在处理到 \(i\) 时,\(j\) 指针继承 \(i-1\) 的状态,再调整到合法的位置。
定义 \(fail_p\) 数组表示从 \(\text{trie}\) 树的根节点一直走到 \(p\) 节点表示的字符串 \(s\),从 \(\text{trie}\) 树的根节点一直走到 \(fail_p\) 节点表示的字符串 \(s'\),满足存在 \(s\) 的一段后缀等于 \(s'\) 且 \(s'\) 的长度最大。
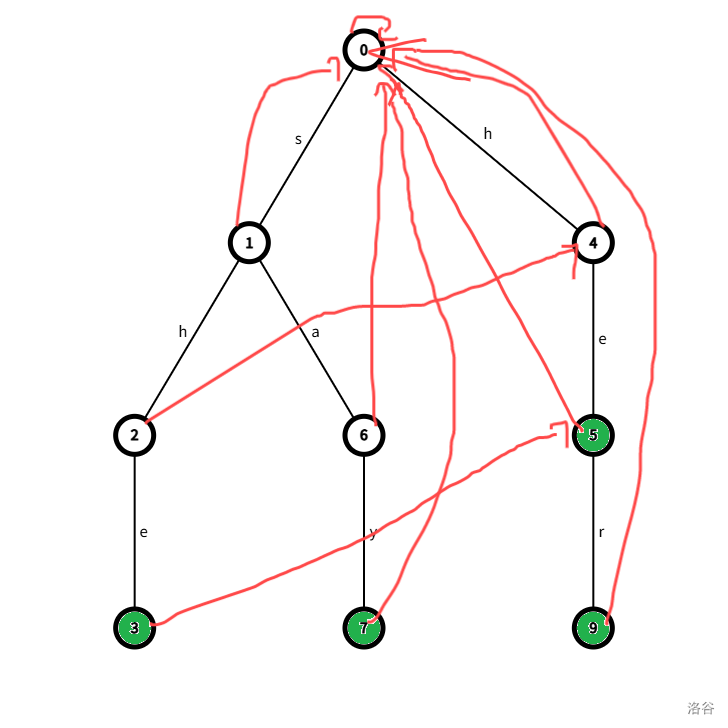
如图,\(fail_3=5\),因为 \(\text{she}\) 的一段后缀 \(\text{s[he]}=\text{he}\),且长度最长。
而 \(fail_2 = 4\),因为 \(\text{sh}\) 的一段后缀 \(\text{s[h]} = \text{h}\),且长度最长。
构建 \(\text{AC}\) 自动机
- 先构建出字典树。
- 使用 \(\text{bfs}\) 从上到下处理出 \(fail\) 数组(特别地,第二层节点的 \(fail\) 都是 \(0\))。
void build()
{
queue<int> Q;
for(int i=0;i<26;++i)
{
if(trie[0][i]) Q.push(trie[0][i]);
}
while(!Q.empty())
{
int pre=Q.front();Q.pop();
for(int i=0;i<26;++i)
{
if(!trie[pre][i]) continue;
int nxt=trie[pre][i];
int j=fail[pre];
while(j&&!trie[j][i]) j=fail[j];
if(trie[j][i]) j=trie[j][i];
fail[nxt]=j;
Q.push(nxt);
}
}
}
这里用到的思想就是 \(\text{kmp}\) 的写法之一。
\(pre\) 代表上一个状态,\(nxt\) 代表当前想要求解的状态,一开始 \(j\) 指针为上一个状态继承过来,然后调整到合法的位置再更新给新的状态。
不断跳 \(fail_j\) 的正确性和 \(\text{kmp}\) 是一样的。
在 AC 自动机上匹配
和建立的原理相似,使用 \(i\) 指针表示在文本串中的位置,\(j\) 指针表示匹配的最长前缀,每次匹配后跳 \(fail\) 即可求得所有模式串中前缀的匹配情况。
int query(string s)
{
int res=0;
for(uint i=0,j=0;i<s.size();++i)
{
int c=s[i]-'a';
while(j&&!trie[j][c]) j=fail[j];
if(trie[j][c]) j=trie[j][c];
int p=j;
while(p&&cnt[p]!=-1)
{
res+=cnt[p];
cnt[p]=-1;
p=fail[p];
}
}
return res;
}
trie 图优化
上列做法的瓶颈在于如果失配就会跳 \(fail\) 指针,这样虽然不影响复杂度但会导致常数增大,如果能够一步到位就好了。
于是可以用路径压缩的思想,将 \(\text{trie}\) 树建成一个 \(\text{trie}\) 图,建出辅助转移的边实现一步到位。
具体地,考虑归纳思想,假设我们已经处理出了 \(i-1\) 层所有的 \(fail\) 和 \(\text{trie}\) 图,那么在处理 \(i\) 层节点是分情况讨论:
假设当前字符为 \(c\),上一层节点编号为 \(pre\)。
- \(trie_{pre,c}\) 不存在,说明此时要跳 \(fail\) 数组,由于上面的都是一步到位的结果,最终一定会跳到 \(trie_{fail_{pre},c}\)。
- \(trie_{pre,c}\) 存在,此时要更新 \(fail\) 数组,将该节点的 \(fail\) 设为 \(trie_{fail_{pre},c}\) 即可。
void build()
{
queue<int> Q;
for(int i=0;i<26;++i)
{
if(trie[0][i]) Q.push(trie[0][i]);
}
while(!Q.empty())
{
int pre=Q.front();Q.pop();
for(int i=0;i<26;++i)
{
int nxt=trie[pre][i];
if(!nxt)
{
trie[pre][i]=trie[fail[pre]][i];
}
else
{
fail[nxt]=trie[fail[pre]][i];
Q.push(nxt);
}
}
}
}
此时查询就可以直接一步到位了。
int query(string s)
{
int res=0;
for(uint i=0,j=0;i<s.size();++i)
{
int c=s[i]-'a';
j=trie[j][c];
int p=j;
while(p&&cnt[p]!=-1)
{
res+=cnt[p];
cnt[p]=-1;
p=fail[p];
}
}
return res;
}
由于 \(\text{trie}\) 图的代码更简单并且在字符集较小的情况下效率高,一般采用 \(\text{trie}\) 图写法。
应用
P3808 AC 自动机(简单版)
\(\text{AC}\) 自动机最简单的板子。
P3796 AC 自动机(简单版 II)
加强版的弱化版,每次匹配的时候可以暴力跳 \(fail\),由于数据过水可以 \(\color{green}\text{AC}\)。
P5357 【模板】AC 自动机
这才是真正的板子。
对比上一题,本题 不保证模式串不同,同时卡掉了暴力跳 \(fail\)(毕竟本身复杂度就是 \(\Theta(nm)\))。
对于模式串相同,可以只匹配一次,建立并查集即可。
想要不暴力跳 \(fail\),考虑建出失配树,不难发现暴力的修改方式修改了 \(p \rightsquigarrow root\) 的一段路径,故只需要在失配树上树上差分即可。
P9196 [JOI Open 2016] 销售基因链 / Selling RNA Strands
题目大意:后缀包含 \(s_1\),前缀包含 \(s_2\) 的文本串数量。
不妨将模式串视为 \(p_2 + \text{特殊字符} + p_1\) ,文本串视为 \(s + \text{特殊字符} + s\),这样直接放在 \(\text{AC}\) 自动机上就做完了。
正确性:由于 \(\text{特殊字符}\) 是字符集以外的字符,模式串能匹配当且仅当 \(p_2\) 是 \(s\) 的后缀,\(p_1\)是 \(s\) 的前缀。
时间复杂度 \(\Theta(|\Sigma|\sum |s|)\)。
后缀数组
定义
记号:记后缀 \(i\) 表示字符串 \(s[i \ldots n]\)。
对于字符串 \(s\),定义两个数组 \(sa,rk\),其中 \(sa[i]\) 表示排名为 \(i\) 的所有后缀中的后缀 \(j\) 的 \(j\),\(rk[i]\) 表示后缀 \(i\) 在所有后缀中的排名。
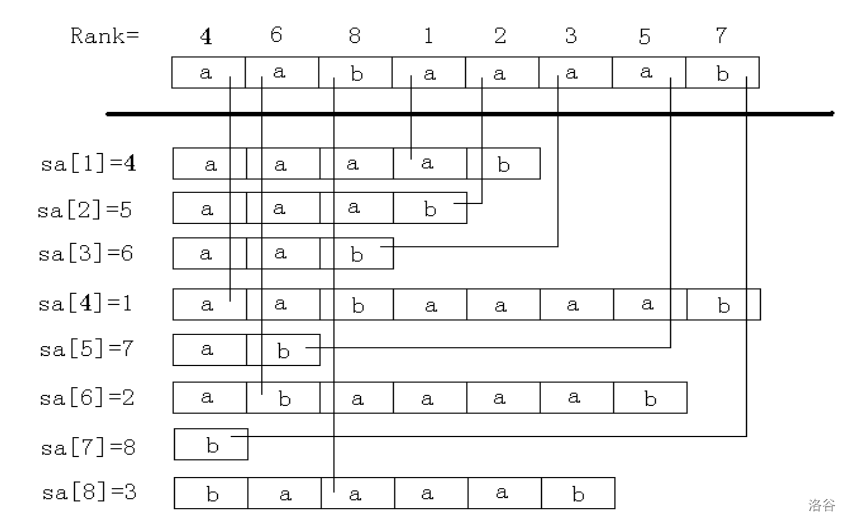
求法
使用了倍增的思想,具体实现用快排是 \(\Theta(n \log^2 n)\) 的,用基数排序是 \(\Theta(n \log n)\) 的。
考虑倍增长度 \(len\),每次排序子串 \(s[i\ldots i+2^{len+1}-1]\),长度不足的用空字符填充,这样进行 \(\log n\) 轮排序就得到了 \(sa\) 数组。
具体地,我们在排序中间维护两个数组 \(sa,rk\),\(rk[i]\) 表示 \(s[i\ldots i+2^{len}-1]\) 的排名,\(sa[i]\) 表示排名为 \(i\) 的后缀是哪个。
如何快速对比两个字符串的字典序大小,只需要分解为 \(len-1\) 的两个子问题,先比较 \(rk[a],rk[b]\) 如果相等则比较 \(rk[a+len],rk[b+len]\),这样做一次双关键字排序。
优化
考虑将快速排序换成双关键字的基数排序。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号