ABC 345 F - Many Lamps

ABC 345 F - Many Lamps

解题思路:

每次选取一条边，要么亮两个，要么灭两个，要么一灭一暗。亮的个数的奇偶性不变，所以不可能亮奇数个。

考虑每个连通块。如果是偶数个一定能全亮，奇数个则最少一个不亮。

对于两暗的，需要时通过操作点亮是一定的。

考虑一明一暗时是加入边的操作意味什么：意味着将明暗位置互换。

考虑这么一副图：

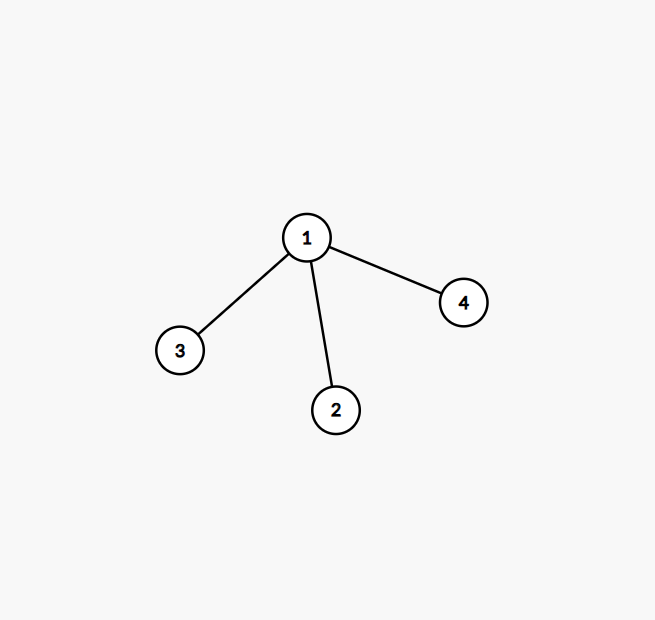
如何点亮所有点？\((1,3),(1,2),(1,4)\)全点即可。

\((1,3),(1,2)\)能够使得不相连的\((2,3)\)点亮。所以两个间接连通的点总能通过他们之间的边传递，使得只有这两点被点亮。

深度优先搜索时，这样考虑。如果儿子结点中有奇数个结点，那么父节点和儿子结点间的边一定加入。

这个加入要么会同时点亮父亲和儿子；要么会将其他奇数结点子树中的结点和当前子节点间接连通点亮，解放父节点，使父节点可以和接下来的子树进行配对或转移。

总之被点亮的点数不会减少，解放当前子树。

代码:

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<ll, ll>;
#define fi first
#define se second
using piii = pair<ll, pair<ll, ll>>;
const ll inf = 1ll << 60;
using ull = unsigned long long;
const int N = 2e5 + 10;
bool vis[N];
vector<pii> e[N];
int siz[N];
bool f[N];
void solve()
{
    int n, m, k;
    cin >> n >> m >> k;
    for (int i = 1; i <= m; i++)
    {
        int a, b;
        cin >> a >> b;
        e[a].emplace_back(b, i);
        e[b].emplace_back(a, i);
    }
    if (k & 1)
    {
        cout << "No\n";
    }
    else
    {
        vector<int> ans;
        for (int i = 1; i <= n; i++)
        {
            if (!vis[i])
            {
                auto dfs = [&](auto self, int u) -> void
                {
                    siz[u] = 1;
                    vis[u] = true;
                    for (auto [v, id] : e[u])
                    {
                        if (vis[v])
                        {
                            continue;
                        }
                        self(self, v);
                        if ((siz[v] & 1) && k > 0)
                        {
                            ans.emplace_back(id);
                            if (!f[u])
                            {
                                k -= 2;
                            }
                            f[u] ^= 1;
                        }
                        siz[u] += siz[v];
                    }
                };
                dfs(dfs, i);
            }
        }
        if (k)
        {
            cout << "No\n";
        }
        else
        {
            cout << "Yes\n";
            cout << ans.size() << endl;
            for (auto x : ans)
            {
                cout << x << " \n"[x == ans.back()];
            }
        }
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    // cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}