Educational Codeforces Round 162 (Rated for Div. 2)
Educational Codeforces Round 162 (Rated for Div. 2)
A - Moving Chips
解题思路:
模拟一下,不难发现是\(1\)之间\(0\)的个数。
代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<ll, ll>;
#define fi first
#define se second
using i128 = __int128_t;
using piii = pair<ll, pair<ll, ll>>;
void solve()
{
int n;
cin >> n;
vector<int> a(n + 1);
int l = -1;
int r = -1;
int cnt = 0;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
if (a[i] == 1 && l == -1)
{
l = i;
}
if (a[i] == 1)
{
r = i;
}
if (l != -1 && a[i] == 0)
{
cnt++;
}
}
for (int i = n; i; i--)
{
if (i > r)
{
if (a[i] == 0)
{
cnt--;
}
}
else
{
break;
}
}
cout << cnt << endl;
}
int main()
{
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}
B - Monsters Attack!
解题思路:
因为是一起靠近\(0\),所以正负无所谓,我们只要没有在这个距离前干掉怪物就寄。
所以比较累计伤害和怪物的累计生命值即可。
代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<ll, ll>;
#define fi first
#define se second
using i128 = __int128_t;
using piii = pair<ll, pair<ll, ll>>;
void solve()
{
ll n, k;
cin >> n >> k;
vector<pii> a(n + 1);
for (int i = 1; i <= n; i++)
{
cin >> a[i].se;
}
for (int i = 1; i <= n; i++)
{
cin >> a[i].fi;
a[i].fi = abs(a[i].fi);
}
sort(a.begin() + 1, a.end());
ll res = 0;
ll cur = 0;
for (int i = 1; i <= n; i++)
{
ll d = a[i].fi - a[i - 1].fi;
res += d * k;
cur += a[i].se;
if (res < cur)
{
puts("NO");
return;
}
}
puts("YES");
}
int main()
{
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}
C - Find B
解题思路:
如果区间没有\(1\),我们可以将值累积到一个位置上,其余位置都是\(1\).
如果区间有\(1\),我们起码要将他们全部变为\(2\),剩下没有\(1\)的位置同上操作。
所以,我们要比较区间\(1\)的数量和能赋给\(1\)的值。
代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<ll, ll>;
#define fi first
#define se second
using i128 = __int128_t;
using piii = pair<ll, pair<ll, ll>>;
void solve()
{
int n, q;
cin >> n >> q;
vector<ll> a(n + 1), s(n + 1), cnt(n + 1);
for (int i = 1; i <= n; i++)
{
cin >> a[i];
cnt[i] = cnt[i - 1];
if (a[i] == 1)
{
cnt[i]++;
}
s[i] = s[i - 1] + a[i] - 1;
}
while (q--)
{
int l, r;
cin >> l >> r;
if (l == r)
{
puts("NO");
continue;
}
ll x = s[r] - s[l - 1];
ll y = cnt[r] - cnt[l - 1];
if (x >= y)
{
puts("YES");
}
else
{
puts("NO");
}
}
}
int main()
{
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}
D - Slimes
解题思路:
如果要想吃掉\(a_i\),起码连续区间的和要大于\(a_i\),所以分别找到左右刚好大于\(a_i\)的连续段。这里可用二分。
如果该连续段长度为\(1\),那么可以直接吞掉。
否则,我们要考虑该连续段是否可以融合得到。
如果该连续段中的数字都一样,那么这个连续段显然无法进行融合,更不要谈吞掉\(a_i\)。
所以,我们分别预处理出每个数字左边和右边第一个和它不同的数字所在的位置,就可以\(O(1)\)判断出合法情况。
若当前大于\(a_i\)的连续段区间为\((l,r), i = r + 1\)。但是\(r\)左边第一个和\(a_r\)不同的数字在\(l - 2\),那么我们答案区间就是\((l-2, r)\)。
当然,如果这个不同数在区间内,那么答案就是\((l,r)\)。
左右分别寻找,取最小。
代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<ll, ll>;
#define fi first
#define se second
using i128 = __int128_t;
using piii = pair<ll, pair<ll, ll>>;
void solve()
{
int n;
cin >> n;
vector<ll> a(n + 10), s(n + 10), lv(n + 10, 0), rv(n + 10, 1e9 + 1);
for (int i = 1; i <= n; i++)
{
cin >> a[i];
s[i] = s[i - 1] + a[i];
}
for (int i = 2; i <= n; i++)
{
if (a[i - 1] != a[i])
{
lv[i] = i - 1;
}
else
{
lv[i] = lv[i - 1];
}
}
for (int i = n - 1; i > 0; i--)
{
if (a[i + 1] != a[i])
{
rv[i] = i + 1;
}
else
{
rv[i] = rv[i + 1];
}
}
vector<int> ans(n + 1, -1);
auto solve_right = [&](int i)
{
int res = -1;
int l = i;
int r = n + 1;
while (l + 1 < r)
{
int mid = l + r >> 1;
if (s[mid] - s[i] > a[i])
{
r = mid;
}
else
{
l = mid;
}
}
if (s[r] - s[i] <= a[i])
{
return -1;
}
int len = r - (i + 1) + 1;
if (len == 1)
{
res = 1;
}
else if (rv[i + 1] <= n)
{
if (rv[i + 1] <= r)
{
res = len;
}
else
{
res = rv[i + 1] - i;
}
}
return res;
};
auto solve_left = [&](int i) -> int
{
int res = -1;
int l = 0;
int r = i;
while (l + 1 < r)
{
int mid = l + r >> 1;
if (s[i - 1] - s[mid] > a[i])
{
l = mid;
}
else
{
r = mid;
}
}
if (s[i - 1] - s[l] <= a[i])
{
return -1;
}
int len = i - 1 - l;
if (len == 1)
{
res = 1;
}
else if (lv[i - 1] > 0)
{
if (l + 1 <= lv[i - 1])
{
res = len;
}
else
{
res = i - 1 - lv[i - 1] + 1;
}
}
return res;
};
// cout << solve_left(3) << endl;
for (int i = 1; i <= n; i++)
{
if (i > 1)
{
int res = solve_left(i);
if (res != -1)
{
if (ans[i] == -1)
{
ans[i] = res;
}
else
{
ans[i] = min(ans[i], res);
}
}
}
if (i < n)
{
int res = solve_right(i);
if (res != -1)
{
if (ans[i] == -1)
{
ans[i] = res;
}
else
{
ans[i] = min(ans[i], res);
}
}
}
}
for (int i = 1; i <= n; i++)
{
cout << ans[i] << ' ';
}
cout << endl;
}
int main()
{
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}
E - Count Paths
解题思路:
考虑当前节点\(u\)作为简单路径经过点,\(v\)为\(u\)的子节点。
对于颜色\(c[u]\)美丽简单路径的计算:
对于两端颜色为\(c[u]\)的简单路径,点\(u\)显然需要作为端点。
所以,当前结点关于颜色\(c[u]\)对答案的总贡献为:以结点\(v\)为根结点的子树中,颜色为\(c[u]\)的结点,且该节点与结点\(u\)之间不存在颜色为\(c[u]\)结点,的结点数量之和。
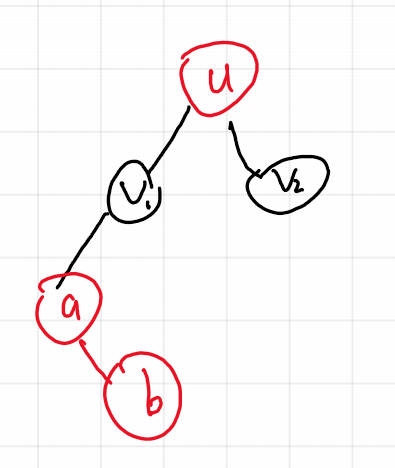
如上图所示,子树\(v_1\)中结点\(a, b\)都和结点\(u\)颜色相同,但\(b\)和\(u\)之间有一个\(a\),所以子树\(v_1\)对于节点\(u\)而言,\(c[u]\)颜色的美丽简单路径只有\((u, a)\)这一条。从递归的角度,就是对于每个结点而言,递归到自己\(i\)后,子树\(i\)中颜色为\(c[i]\)的个数我们置为\(1\)即可,因为除了自己,下面颜色为\(c[i]\)的结点与上面颜色为\(c[i]\)的结点之间都有一个自己。
对于颜色不是\(c[u]\)美丽简单路径的计算:
对于两端颜色不是\(c[u]\)的简单路径,点\(u\)显然需要作为中间节点。
那么对于该颜色的美丽简单路径的数量的统计,就是子树之间结点颜色个数根据乘法原理相乘,然后累加得到。
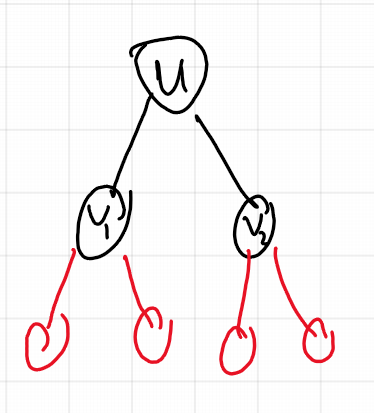
如上图所示,子树\(v_1\)有\(2\)个该颜色结点,\(v_2\)同样,答案就是\(2 \times 2 = 4\)。更多子树的话,还要继续乘。
实现代码1(启发式合并)\(O(nlog^2n)\):
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<ll, ll>;
#define fi first
#define se second
using i128 = __int128_t;
using piii = pair<ll, pair<ll, ll>>;
const int N = 2e5 + 10;
vector<int> e[N];
int c[N];
int n;
map<int, ll> dp[N];
ll ans;
void dfs(int u, int fa)
{
dp[u][c[u]] = 1;
for (auto v : e[u])
{
if (v == fa)
{
continue;
}
dfs(v, u);
if (dp[v].contains(c[u]))
{
ans += dp[v][c[u]];
dp[v].erase(c[u]);
}
// 启发式合并
// 每个点最多被计算log次
if (dp[v].size() > dp[u].size())
{
dp[u].swap(dp[v]);
}
for (auto t : dp[v])
{
if (dp[u].contains(t.fi))
{
ans += dp[u][t.fi] * dp[v][t.fi];
}
dp[u][t.fi] += dp[v][t.fi];
}
}
}
void solve()
{
ans = 0;
cin >> n;
for (int i = 1; i <= n; i++)
{
dp[i].clear();
cin >> c[i];
vector<int>().swap(e[i]);
}
for (int i = 1; i < n; i++)
{
int a, b;
cin >> a >> b;
e[a].push_back(b);
e[b].push_back(a);
}
dfs(1, -1);
cout << ans << endl;
}
int main()
{
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}
实现代码2(构建虚树)\(O(nlogn)\):
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<ll, ll>;
#define fi first
#define se second
using i128 = __int128_t;
using piii = pair<ll, pair<ll, ll>>;
const int N = 2e5 + 10;
vector<int> e[N], adj[N];
ll dp[N];
int n;
int c[N];
vector<int> color[N];
int dep[N];
int dfn[N];
int fa[N][22];
int idx;
int s[N];
int top;
ll ans = 0;
void dfs(int u, int par)
{
fa[u][0] = par;
dfn[u] = ++idx;
for (auto v : e[u])
{
if (v == par)
{
continue;
}
dep[v] = dep[u] + 1;
dfs(v, u);
}
vector<int>().swap(e[u]);
}
int lca(int a, int b)
{
if (dep[a] < dep[b])
{
swap(a, b);
}
for (int i = 20; i >= 0; i--)
{
if (dep[fa[a][i]] >= dep[b])
{
a = fa[a][i];
}
}
if (a == b)
{
return a;
}
for (int i = 20; i >= 0; i--)
{
if (fa[a][i] != fa[b][i])
{
a = fa[a][i];
b = fa[b][i];
}
}
return fa[a][0];
}
bool cmp(int a, int b)
{
return dfn[a] < dfn[b];
}
void build(vector<int> a)
{
sort(a.begin(), a.end(), cmp);
top = 0;
s[++top] = 1;
if (a[0] != 1)
{
s[++top] = a[0];
}
for (int i = 1; i < a.size(); i++)
{
int l = lca(s[top], a[i]);
while (top > 1 && dep[s[top - 1]] >= dep[l])
{
adj[s[top - 1]].push_back(s[top]);
top--;
}
if (s[top] != l)
{
adj[l].push_back(s[top]);
s[top] = l;
}
s[++top] = a[i];
}
while (top)
{
adj[s[top - 1]].push_back(s[top]);
top--;
}
}
void dfs_solve(int u, int col)
{
dp[u] = (c[u] == col);
for (auto v : adj[u])
{
dfs_solve(v, col);
if (c[u] != col)
{
ans += dp[v] * dp[u];
}
else
{
ans += dp[v];
}
dp[u] += dp[v];
}
if (c[u] == col)
{
dp[u] = 1;
}
vector<int>().swap(adj[u]);
}
void solve()
{
idx = 0;
ans = 0;
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> c[i];
color[c[i]].push_back(i);
}
for (int i = 1; i < n; i++)
{
int a, b;
cin >> a >> b;
e[a].push_back(b);
e[b].push_back(a);
}
dep[1] = 1;
dfs(1, -1);
for (int j = 1; j <= 20; j++)
{
for (int i = 1; i <= n; i++)
{
fa[i][j] = fa[fa[i][j - 1]][j - 1];
}
}
for (int i = 1; i <= n; i++)
{
if (color[i].size() == 0)
{
continue;
}
build(color[i]);
dfs_solve(1, i);
vector<int>().swap(color[i]);
}
cout << ans << endl;
}
int main()
{
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号