Toyota Programming Contest 2024#1(AtCoder Beginner Contest 337)
Toyota Programming Contest 2024#1(AtCoder Beginner Contest 337)
A - Scoreboard
代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<ll, ll>;
#define fi first
#define se second
using i128 = __int128_t;
void solve()
{
int n;
cin >> n;
int x = 0;
int y = 0;
for (int i = 1; i <= n; i++)
{
int a, b;
cin >> a >> b;
x += a;
y += b;
}
int ans = x - y;
if (ans > 0)
{
puts("Takahashi");
}
else if (ans < 0)
{
puts("Aoki");
}
else
{
puts("Draw");
}
}
int main()
{
int t = 1;
// cin >> t;
while (t--)
{
solve();
}
return 0;
}
B - Extended ABC
代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<ll, ll>;
#define fi first
#define se second
using i128 = __int128_t;
void solve()
{
string s;
cin >> s;
int n = s.size();
for (int i = 1; i < n; i++)
{
if (s[i] < s[i - 1])
{
puts("No");
return;
}
}
puts("Yes");
}
int main()
{
int t = 1;
// cin >> t;
while (t--)
{
solve();
}
return 0;
}
C - Lining Up 2
解题思路:
\(dfs\)一次即可。
代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<ll, ll>;
#define fi first
#define se second
using i128 = __int128_t;
void solve()
{
int n;
cin >> n;
vector<vector<int>> adj(n + 1);
int r = 0;
for (int i = 1; i <= n; i++)
{
int x;
cin >> x;
if (x == -1)
{
r = i;
}
else
{
adj[x].push_back(i);
}
}
auto dfs = [&](auto self, int u) -> void
{
cout << u << ' ';
for (auto v : adj[u])
{
self(self, v);
}
};
dfs(dfs, r);
}
int main()
{
int t = 1;
// cin >> t;
while (t--)
{
solve();
}
return 0;
}
D - Cheating Gomoku Narabe
解题思路:
记录时,\(o\)为1,其余为0.
\(a[i][j]:记录以第i行第j列为末尾,总长度为k的序列的区间和。\)
遍历时,\(x为-1\),其余为\(1\)。遍历过程中,长度为\(k\)的区间和刚好为\(k\)时,\(k - a[i][j]\)就是一种填补数量。
横着跑一次,竖着跑一次。
时间复杂度\(O(n)\).
代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<ll, ll>;
#define fi first
#define se second
using i128 = __int128_t;
void solve()
{
int h, w, k;
cin >> h >> w >> k;
vector<string> g(h + 1);
for (int i = 1; i <= h; i++)
{
cin >> g[i];
g[i] = ' ' + g[i];
}
vector<vector<int>> a(h + 1, vector<int>(w + 1));
int cur = 0;
for (int i = 1; i <= h; i++)
{
cur = 0;
queue<int> q;
for (int j = 1; j <= w; j++)
{
if (q.size() == k)
{
cur -= q.front();
q.pop();
}
int x = 0;
if (g[i][j] == 'o')
{
x = 1;
}
q.push(x);
cur += x;
if (q.size() == k)
{
// cout << i << ' ' << j << ' ' << cur << endl;
a[i][j] = cur;
}
}
}
int ans = 1e9;
for (int i = 1; i <= h; i++)
{
cur = 0;
queue<int> q;
for (int j = 1; j <= w; j++)
{
if (q.size() == k)
{
cur -= q.front();
q.pop();
}
int x = 1;
if (g[i][j] == 'x')
{
x = -1;
}
q.push(x);
cur += x;
if (q.size() == k)
{
if (cur == k)
{
ans = min(k - a[i][j], ans);
}
}
}
}
for (int i = 1; i <= w; i++)
{
cur = 0;
queue<int> q;
for (int j = 1; j <= h; j++)
{
if (q.size() == k)
{
cur -= q.front();
q.pop();
}
int x = 0;
if (g[j][i] == 'o')
{
x = 1;
}
q.push(x);
cur += x;
if (q.size() == k)
{
// cout << i << ' ' << j << ' ' << cur << endl;
a[j][i] = cur;
}
}
}
for (int i = 1; i <= w; i++)
{
cur = 0;
queue<int> q;
for (int j = 1; j <= h; j++)
{
if (q.size() == k)
{
cur -= q.front();
q.pop();
}
int x = 1;
if (g[j][i] == 'x')
{
x = -1;
}
q.push(x);
cur += x;
if (q.size() == k)
{
if (cur == k)
{
ans = min(k - a[j][i], ans);
}
}
}
}
if (ans > k)
{
ans = -1;
}
cout << ans << endl;
}
int main()
{
int t = 1;
// cin >> t;
while (t--)
{
solve();
}
return 0;
}
E - Bad Juice
解题思路:
每个人第二天出问题或者没出问题对应二进制变化\(1或者0\)。
所以有\(n\)杯果汁,我们就需要\(n\)中不同的二进制编码。每种唯一即可对应情况选择出坏的果汁。
代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<ll, ll>;
#define fi first
#define se second
using i128 = __int128_t;
void solve()
{
int n;
cin >> n;
n--;
int m = 0;
for (int i = 30; i >= 0; i--)
{
if (n >> i & 1)
{
cout << i + 1 << endl;
m = i + 1;
break;
}
}
vector<vector<int>> a(m + 10, vector<int>(0));
for (int i = 1; i <= n; i++)
{
for (int j = 0; j < 30; j++)
{
if (i >> j & 1)
{
a[j + 1].push_back(i + 1);
}
}
}
for (int i = 1; i <= m; i++)
{
cout << a[i].size() << ' ';
for (auto x : a[i])
{
cout << x << ' ';
}
if (a[i].size() == 0)
{
continue;
}
cout << endl;
}
cout.flush();
string s;
cin >> s;
int ans = 1;
for (int i = 0; i < s.size(); i++)
{
if (s[i] == '1')
{
ans += 1 << i;
}
}
cout << ans << endl;
cout.flush();
}
int main()
{
int t = 1;
// cin >> t;
while (t--)
{
solve();
}
return 0;
}
G - Tree Inversion
解题思路:
看到求\(f(1)...f(n)\),思路开始向换根\(dp\)尝试。
首先,我们如何求出以\(1\)为根节点的有根树\(f[u]\)。
求\(u \to v\)路径中\(w\)的数量,就是求\(u \to v\)路径中,有多少个数字严格大于\(v\)。也就是说,沿着路径记录下来的所有结点编号集合中,有多少个数字是大于\(v\)的。
这个我们可以用树状数组来实时求取,先查再插再删。
这样我们\(f[1]\)就求得了。
接下来思考换根。
下图中,红色为子树\(2\),蓝色为子树\(1\)
假设初始图如下:
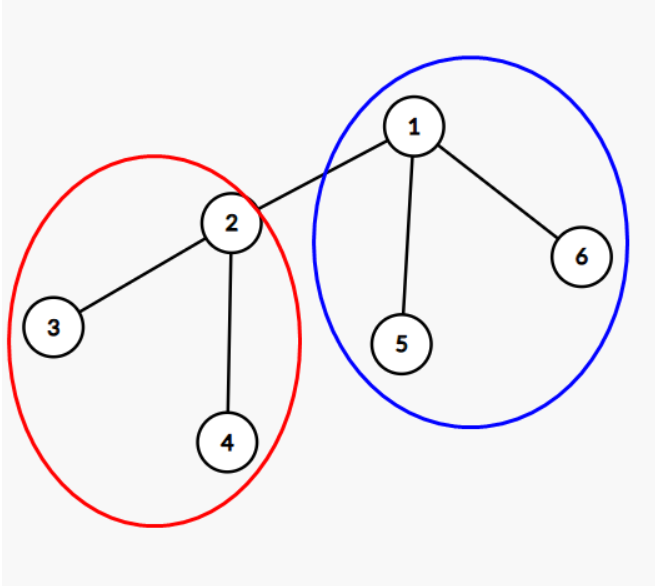
换根后如下:
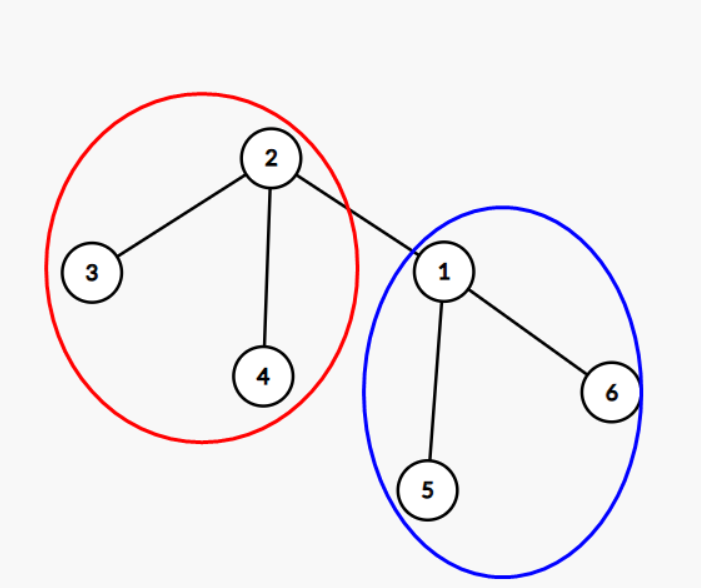
)
我们发现,换根后对于子树\(2\)来说,失去了结点\(1\)对于自己的贡献。所以,我们要得到子树\(2\)中结点编号小于\(1\)的结点个数\(a\)。
对于子树\(1\)来说,增加了结点\(2\)对于自己的贡献,所以,我们要得到子树\(1\)中结点编号小于\(2\)的结点个数\(b\)。
除上述两点外,整棵树并未有其他贡献,所以整体变化量为\(x = b - a\)。
所以,\(f[2] = f[1] + x\)。
对上述特例进行扩展。遍历过程中,结点\(1\)可看作父节点\(u\),结点\(2\)可看作子节点\(v\)。
如何求得一棵子树中所有结点编号在某个数值区间中的出现个数?
这里我们选择主席树。(据说有启发式合并解法)
有了树链剖分思想,求得子树\(2\)中的情况很容易,因为\(dfs\)序连续地包括住了他。但是子树\(1\)如何操作呢?
由于我们是以结点\(1\)为根节点建立的主席树,所以图中的子树\(1\)在\(dfs\)序上并不连续。
当然,这里我们可以选择将子树\(1\)分为两个区间进行查询:
ll x = query(rt[lf[v] - 1], rt[0], 1, n, 1, v) + query(rt[dfn], rt[rf[v]], 1, n, 1, v) - query(rt[rf[v]], rt[lf[v] - 1], 1, n, 1, u);
但其实还有较为简单地方法。
如果当前子树根节点编号为\(v\),那么整个图中编号小于等于\(v\)的结点数一共只有\(v\)个。所以,我们用\(v\)减去子树\(v\)中小于等于\(v\)的结点个数,得到的就是父节点子树中编号小于\(v\)的结点个数了。
代码:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<ll, ll>;
#define fi first
#define se second
using i128 = __int128_t;
const int N = 2E5 + 10;
vector<vector<int>> adj(N);
int tr[N];
int n;
ll sum = 0;
int ls[N * 22];
int rs[N * 22];
int lf[N];
int rf[N];
int idx = 0;
int dfn = 0;
int t[N * 22];
int rt[N];
ll ans[N];
int lowbit(int x)
{
return x & -x;
}
void insert(int x, int val)
{
for (int i = x; i <= n; i += lowbit(i))
{
tr[i] += val;
}
}
int query(int x)
{
int res = 0;
for (int i = x; i; i -= lowbit(i))
{
res += tr[i];
}
return res;
}
void update(int &u, int pre, int l, int r, int val)
{
if (u == 0)
{
u = ++idx;
}
t[u] = t[pre] + 1;
if (l == r)
{
return;
}
int mid = l + r >> 1;
if (val <= mid)
{
rs[u] = rs[pre];
update(ls[u], ls[pre], l, mid, val);
}
else
{
ls[u] = ls[pre];
update(rs[u], rs[pre], mid + 1, r, val);
}
}
int query(int &u, int pre, int l, int r, int tl, int tr)
{
// cout << u << ' ' << l << ' ' << r << ' ' << t[u] << ' ' << t[pre] << endl;
if (tl <= l && tr >= r)
{
return t[u] - t[pre];
}
int res = 0;
int mid = l + r >> 1;
if (tl <= mid)
{
res += query(ls[u], ls[pre], l, mid, tl, tr);
}
if (tr > mid)
{
res += query(rs[u], rs[pre], mid + 1, r, tl, tr);
}
return res;
}
void dfs1(int u, int fa)
{
sum += query(n) - query(u);
insert(u, 1);
lf[u] = ++dfn;
// cout << u << ' ' << dfn << ' ' << ls[u] << endl;
update(rt[dfn], rt[dfn - 1], 1, n, u);
for (auto v : adj[u])
{
if (v == fa)
{
continue;
}
dfs1(v, u);
}
insert(u, -1);
rf[u] = dfn;
}
void dfs2(int u, int fa)
{
ans[u] = sum;
for (auto v : adj[u])
{
if (v == fa)
{
continue;
}
ll x = v - query(rt[rf[v]], rt[lf[v] - 1], 1, n, 1, v) - query(rt[rf[v]], rt[lf[v] - 1], 1, n, 1, u);
// cout << u << ' ' << v << endl;
// cout << v << ' ' << query(rt[rf[v]], rt[lf[v] - 1], 1, n, 1, v) << ' ' << query(rt[rf[v]], rt[lf[v] - 1], 1, n, 1, u) << endl;
sum += x;
dfs2(v, u);
sum -= x;
}
}
void solve()
{
cin >> n;
for (int i = 1; i < n; i++)
{
int u, v;
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs1(1, -1);
// cout << 1 << endl;
dfs2(1, -1);
// cout << ls[2] << endl;
// cout << rs[2] << ' ' << ls[2] << endl;
// cout << query(rt[rf[2]], rt[lf[2] - 1], 1, n, 1, 1) << endl;
for (int i = 1; i <= n; i++)
{
cout << ans[i] << ' ';
}
}
int main()
{
int t = 1;
// cin >> t;
while (t--)
{
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号