2020ICPC区域赛南京站
2020ICPC区域赛南京站
K Co-prime Permutation
解题思路:
首先,根据样例2不难发现,\(k\)的下界为\(1\),因为1和排列中的任何数都会互质。
其次,我们考虑下上界大概是多少,也就是\(k = n\)是否一定合法。
假设,我们有一个初识排列\(p_i = i\).此时我们有\(1\)个元素和他的下标互质。
根据经验,我们将升序排列的元素向左错位一个偏移量就会得到\(p_1 = 2,p_2 = 3,...,p_n = 1\).此时,有\(n\)个元素和下标互质。
如果我们要恰好\(k\)个元素和下标互质,那么我们将前\(k\)个数看作一个环,同时向左错位一个偏移量即可。
注意,\(k=1\)的情况要特判。该情况上面也已经讨论过。
代码:
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
ll gcd(ll a,ll b)
{
return b ? gcd(b,a %b): a;
}
void solve()
{
int n,k;
scanf("%d %d",&n,&k);
if(k == 0)
{
puts("-1");
}
else if(k == 1)
{
for(int i = 1;i<=n;i++)
{
printf("%d ",i);
}
}
else
{
vector<int> a(n + 1);
int cnt = 2;
for(int i = 1;i<=k;i++)
{
a[i] = cnt ++;
if(cnt > k)
{
cnt = 1;
}
}
for(int i = k + 1;i<=n;i++)
{
a[i] = i;
}
cnt = 0;
for(int i = 1;i<=n;i++)
{
printf("%d ",a[i]);
}
}
}
int main()
{
int t = 1;
while(t--)
{
solve();
}
return 0;
}
L Let's Play Curling
解题思路:
稍微写一下样例,不难发现,能对答案产生贡献的红球之间没有一个蓝球。
所以,本题能够转化为,没两蓝球之间的最大红球个数。
排序后,双指针遍历即可。
代码:
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int n,m;
void solve()
{
scanf("%d %d",&n,&m);
vector<int> a(n + 1),b(m + 1);
unordered_map<int,int> q;
for(int i = 1;i<=n;i++)
{
scanf("%d",&a[i]);
q[a[i]] ++;
}
for(int i = 1;i<=m;i++)
{
scanf("%d",&b[i]);
}
sort(a.begin() + 1,a.end());
sort(b.begin() + 1,b.end());
a.erase(unique(a.begin() + 1,a.end()),a.end());
b.erase(unique(b.begin() + 1,b.end()),b.end());
int i = 1;
int j = 1;
ll ans = 0;
n = a.size() - 1;
m = b.size() - 1;
// for(int i = 1;i<=n;i++)
// {
// cout<<a[i]<<' ';
// }
// cout<<endl;
// for(int i= 1;i<=m;i++)
// {
// cout<<b[i]<<' ';
// }
// cout<<endl;
while(i <= n && j <= m)
{
ll cnt = 0;
while(j <= m && b[j] <= a[i])
{
if(a[i] == b[j])
{
i ++;
j ++;
}
else
{
j ++;
}
}
if(j > m)
{
break;
}
while(i <= n && a[i] <= b[j])
{
// cout<<i<<' '<<a[i]<<endl;
if(a[i] == b[j])
{
i ++;
j ++;
ans = max(ans,cnt);
cnt = 0;
continue;
}
else
{
cnt += q[a[i]];
i ++;
}
}
// cout<<i<<' '<<j<<' '<<cnt<<endl;
ans = max(ans,cnt);
}
ll sum = 0;
while(i <= n)
{
sum += q[a[i]];
i ++;
}
ans = max(sum,ans);
if(ans == 0)
{
puts("Impossible");
}
else
{
printf("%lld\n",ans);
}
}
int main()
{
int t = 1;
scanf("%d",&t);
while(t--)
{
solve();
}
return 0;
}
E. Evil Coordinate
解题思路:
如果障碍出现在出发点或者终点,那么一定会碰到障碍。
我们一共有两个维度移动方向,上下和左右。
如果我们只能在一个维度移动,并且障碍出现在起点到终点的线段上,那么一定会碰到障碍。
除此之外,我们都能避开他。
举例:
若移动序列为\(DDUUUUU\),明显终点在\((0,3)\),若障碍设置在\((0,1)\),那一定会经过。但如果障碍设置在\((0,-1)\),我们完全可以先走完上,再走下。
若我们能在两个维度移动,那我们一定能走出两条除了终点和起点外完全不相交的路径。此时,如果障碍会出现在其中一个上,我们走另一条路径必然可以避开障碍。
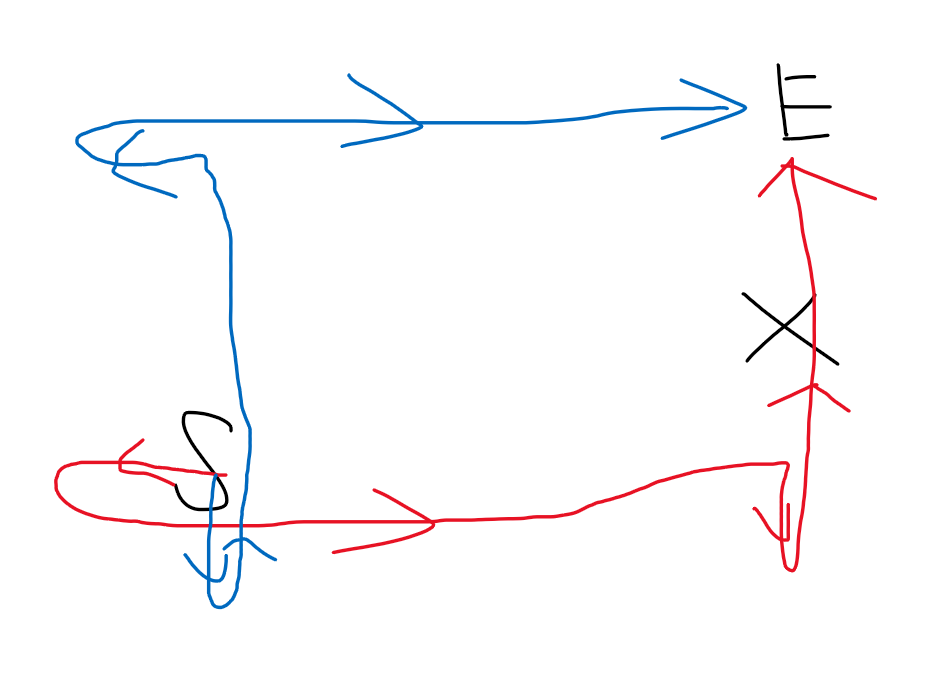
所以,如图,我们可以先走完左右再走上下,全排列枚举行走顺序即可。
代码:
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
unordered_map<int,char> mp;
void init()
{
mp[1] = 'U';
mp[2] = 'D';
mp[3] = 'L';
mp[4] = 'R';
}
void solve()
{
int x,y;
scanf("%d %d",&x,&y);
string s;
cin>>s;
unordered_map<char,int> cnt;
if(x == 0 && y == 0)
{
puts("Impossible");
return ;
}
for(auto c : s)
{
cnt[c] ++;
}
vector<bool> st(10);
auto check = [&](string t)
{
int a = 0;
int b = 0;
for(int i = 0;i<4;i++)
{
for(int j = 1;j<=cnt[t[i]];j++)
{
if(t[i] == 'U')
{
b ++;
}
else if(t[i] == 'D')
{
b --;
}
else if(t[i] == 'L')
{
a --;
}
else
{
a ++;
}
if(a == x && b == y)
{
return false;
}
// cout<<a<<' '<<b<<endl;
}
}
return true;
};
string str = "UDLR";
sort(str.begin(),str.end());
// cout<<str<<endl;
bool f = false;
do
{
if(check(str))
{
f = true;
break;
}
} while(next_permutation(str.begin(),str.end()));
if(f)
{
for(int i = 0;i<4;i++)
{
for(int j = 1;j<=cnt[str[i]];j++)
{
putchar(str[i]);
}
}
puts("");
}
else
{
puts("Impossible");
}
}
int main()
{
init();
int t = 1;
scanf("%d",&t);
while(t--)
{
solve();
}
return 0;
}
F. Fireworks
解题思路:
假设我们造\(k\)个烟花放一次,失败了就再造\(k\)个烟花放一次。
那么单次发烟花的时间为\(nk + m\),若成功的概率期望为\(E\),则下班的最早时间为\((nk + m) \times E\).
因此,我们应当找到最合适的\(k\),使得时间尽量小。
造一个完美烟花的概率为\(p\),造\(k\)个烟花全是不完美的概率为\((1 - p)^k\),那么造\(k\)个烟花至少有一个完美的概率是\(1 - (1-p)^k\).
我们设造\(k\)个烟花至少有一个完美的概率为\(x = 1 - (1 - p)^k\),那么我们第\(s\)次放烟花成功然后下班的概率为\((1-x)^{s-1}x\),即前面放烟花都下班失败,第\(s\)次下班成功。
到这我们发现,这是几何概型。若几何概型中单次实验事件发生概率为\(p\),那么期望\(E = \frac 1 p\).
所以得到方程
我们要求这个方程的局部最小值,二阶导判断该函数具有凹性,然后三分求解即可。
代码:
#include<bits/stdc++.h>
using namespace std;
double n,m,p;
const double eps = 1e-8;
using ll = long long;
void solve()
{
scanf("%lf %lf %lf",&n,&m,&p);
p *= 1e-4;
double l = 1;
double r = 1e18;
auto f = [&](ll k)
{
return (n * k + m) / (1.0 - pow(1.0-p,k));
};
while(l + 1 < r)
{
double mid = (r - l) / 3.0;
double m1 = l + mid;
double m2 = r - mid;
if(f(m1) > f(m2))
{
l = m1;
}
else
{
r = m2;
}
}
ll a = l;
ll b = a + 1;
double ans = min(f(a),f(b));
printf("%.8lf\n",ans);
}
int main()
{
int t = 1;
scanf("%d",&t);
while(t--)
{
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号