数据结构与树论

前言

本博客用于总结联赛中常考的数据结构和树论，大概会写一点树链剖分，\(dsu on tree\)，树状数组，线段树，平衡树，dfs序，树上差分等等。
虽然对于联赛来说，数据结构的意义更多是骗分，但毕竟\(CSP\)不同于\(NOIP\)，万一就想标新立异呢？
也许会附带一些简要的讲解，联赛后有时间会写详细的讲解，但是我真的很懒，所以请不要有过大的期望。

\(\texttt{Talk is cheap.Let me show you the code.}\)

树状数组

树状数组是一种支持区间查询，区间更新，单点查询，单点更新，区间最值，逆序对，区间不同的个数等多种操作的数据结构，复杂度为\(O(nlogn)\)，优点是代码简介，常数非常小，但是不是很好理解。（说实话我觉得树状数组是最好理解的）树状数组的实现和位运算密切相关，也就是\(lowbit\)运算，树状数组最核心的思想是前缀和。

区间查询与单点更新

树状数组1

#include<cstdio>
int n,m,c[500005];
int lowbit(int x)
{
	return x&-x;
}
int query(int pos)
{
	int ans=0;
	for(int i=pos;i>=1;i-=lowbit(i))
	ans+=c[i];
	return ans;
}
void add(int pos,int x)
{
	for(int i=pos;i<=n;i+=lowbit(i))
	c[i]+=x;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		int x;
		scanf("%d",&x);
		add(i,x);
	}
	while(m--)
	{
		int opt,x,y;
		scanf("%d%d%d",&opt,&x,&y);
		if(opt==1)add(x,y);
		else printf("%d\n",query(y)-query(x-1));
	}
	return 0;
}

区间更新与单点查询

树状数组2

这个也很简单，但是我们不能用普通的树状数组来做，初始化的时候并不是在记录初始数组而是差分数组，这样就可以用树状数组1中区间查询的套路来查询单点，这是差分的性质，而至于区间更新\([l,r]\)，只需要在\(r+1\)的地方加上这个值，在\(l\)的地方减去这个值，根据差分的性质，最后就能求出正确答案，重点就是熟悉差分。

有一个小细节，区间更新不能直接像树状数组\(1\)里面写\(l-1\)和\(r\)，应该是\(r+1\)和\(l\)，至于为什么，希望读者自己去思考，深入理解树状数组的实现。

#include<cstdio>
int n,m,c[500005],a[500005];
int lowbit(int x){return x&-x;}
void add(int pos,int x)
{
	for(int i=pos;i<=n;i+=lowbit(i))
	c[i]+=x;
}
int query(int pos)
{
	int ans=0;
	for(int i=pos;i>=1;i-=lowbit(i))
	ans+=c[i];
	return ans;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	scanf("%d",&a[i]),add(i,a[i]-a[i-1]);
	while(m--)
	{
		int opt,x,y,k;
		scanf("%d%d",&opt,&x);
		if(opt==1)
		{
			scanf("%d%d",&y,&k);
			add(x,k),add(y+1,-k);
		}
		else printf("%d\n",query(x));
	}
	return 0;
}

求逆序对

逆序对

想不到吧，还能整这个！

这个思想非常简单，不讲了，只要懂树状数组就能理解。核心就是倒叙\(n~1\)循环，每次给\(ans\)累计\(query(a[i]-1)\)的答案，再在\(a[i]\)的位置加\(1\)，手动模拟一下就可以了，注意一下离散化的排序问题。

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,a[1000005],c[1000005],ans;
int lowbit(int x){return x&-x;}
int query(int pos){int ans=0;for(int i=pos;i>=1;i-=lowbit(i))ans+=c[i];return ans;}
void add(int pos,int x){for(int i=pos;i<=n;i+=lowbit(i))c[i]+=x;}
struct node{int tmp,num;}b[1000005];
bool cmp(node a,node b){return a.tmp<b.tmp||(a.tmp==b.tmp&&a.num<b.num);}
signed main()
{
    ios::sync_with_stdio(false);
    cin>>n;
    for(int i=1;i<=n;i++){cin>>b[i].tmp;b[i].num=i;}
    sort(b+1,b+1+n,cmp);
    for(int i=1;i<=n;i++)a[b[i].num]=i;
    for(int i=n;i>=1;i--)
    ans+=query(a[i]-1),add(a[i],1);
    cout<<ans<<endl;
    return 0;
}

区间不同值

就是求某个区间内一共有多少个不相同的元素。
如果要用树状数组来求这个的话，限制非常多，因为必须使用离线操作，这也就意味着我们无法进行更新操作。

SDOI2010 HH的项链

我们考虑一个序列:\(\texttt{1 2 3 4 3 5}\)，会发现，如果我们要查询一个区间\([l,r]\)，比如\(l=3,r=6\)，此时区间内有\(2\)个元素为\(3\)，但实际上影响我们最终答案的只与后面的那个\(3\)有关。

我们考虑正在查询一个区间\([l,r]\),从\(1\)循环到\(r\)，每遇到一个\(a[i]\)，就\(add(i,1)\),而如果\(a[i]\)这个数在前面的位置\(pre\)出现过，就\(add(pre,-1)\)，再更新\(a[j]\)出现的位置为\(j\),最后直接利用前缀和来查询就可以了。

但你还要考虑一个问题，如果在前面出现的\(r\)比在后面出现的\(r\)要小，那么就会出现错误情况，所以你要把所有的\(r\)从小到大排序。

我觉得讲树状数组很难，因为本来就不适合讲，适合自己画图、模拟去理解。

#include<iostream>
#include<algorithm>
using namespace std;
int n,a[1000005],vis[1000005],p[1000005],c[1000005],q;
struct node{int l,r,ask;}b[1000005];
int lowbit(int x){return x&-x;}
void add(int pos,int x){for(int i=pos;i<=n;i+=lowbit(i))c[i]+=x;}
int query(int pos)
{
	int ans=0;
	for(int i=pos;i>=1;i-=lowbit(i))ans+=c[i];
	return ans;
}
bool cmp(node a,node b){return a.r<b.r;}
int main()
{
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	cin>>q;
	for(int i=1;i<=q;i++){cin>>b[i].l>>b[i].r;b[i].ask=i;}
	sort(b+1,b+1+q,cmp);
	int sta=1;
	for(int i=1;i<=q;i++)
	{
		for(int j=sta;j<=b[i].r;j++)
		{
			add(j,1);
			if(vis[a[j]])add(vis[a[j]],-1);
			vis[a[j]]=j;
		}		
		p[b[i].ask]=query(b[i].r)-query(b[i].l-1);
		sta=b[i].r+1;
	}
	for(int i=1;i<=q;i++)cout<<p[i]<<"\n";
	return 0;
}

树状数组讲到这里就可以了，因为确实功能比较少并且理解复杂。

线段树

线段树1

线段树是一种非常优秀的数据结构，复杂度\(O(nlogn)\)，虽然常数比较大，代码也比较长，只要理解了，还是好写，功能相对非常多，树状数组能做的事情它都能做，除此之外线段树还支持好多好多操作以及优化，慢慢来吧。

区间/单点的加法/查询

线段树支持这四种操作同时进行，虽然树状数组也支持，但写起来很麻烦，其实线段树理解了，也是很好写的。

当然了，细节很重要，比如\(pushdown\)和\(pushup\)的运用等等，而且也要注意常数的问题，结构体的常数一般会大一点，\(\texttt{zkw}\)线段树的常数很小，但我没有学，所以我一般习惯写不带结构体的线段树。

#include<bits/stdc++.h>
using namespace std;
#define int long long 
int n,m,a[100005],t[400005],laz[400005];
void pushdown(int rt,int l,int r)
{
	if(!laz[rt])return;
	int len=(r-l+1);
	laz[rt<<1]+=laz[rt];
	laz[rt<<1|1]+=laz[rt];
	t[rt<<1]+=(len-(len>>1))*laz[rt];
	t[rt<<1|1]+=(len>>1)*laz[rt];
	laz[rt]=0;
	
}
void pushup(int rt){t[rt]=(t[rt<<1]+t[rt<<1|1]);}
void build(int l,int r,int rt)
{
	if(l==r){t[rt]=a[l];return;}
	int mid=(l+r)>>1;
	build(l,mid,rt<<1);
	build(mid+1,r,rt<<1|1);
	pushup(rt);
}
void update(int rt,int l,int r,int la,int ra,int x)
{
	if(la<=l&&r<=ra)
	{
		t[rt]+=(r-l+1)*x;
		laz[rt]+=x;
		return;
	}
	pushdown(rt,l,r);
	int mid=(l+r)>>1;
	if(la<=mid)update(rt<<1,l,mid,la,ra,x);
	if(ra>mid)update(rt<<1|1,mid+1,r,la,ra,x);
	pushup(rt);
}
int query(int rt,int l,int r,int la,int ra)
{
	if(la<=l&&r<=ra)return t[rt];
	pushdown(rt,l,r);
	int mid=(l+r)>>1;
	int ans=0;
	if(la<=mid)ans+=query(rt<<1,l,mid,la,ra);
	if(ra>mid)ans+=query(rt<<1|1,mid+1,r,la,ra);
	return ans;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>a[i];
	build(1,n,1);
	while(m--)
	{
		int opt,x,y,k;
		cin>>opt>>x>>y;
		if(opt&1)cin>>k,update(1,1,n,x,y,k);
		else cout<<query(1,1,n,x,y)<<"\n";
	}
	return 0;
}

区间/单点的乘法/加法/更新

线段树2

其实相对线段树\(1\),只是多了一个乘法的操作而已，多打一个\(lazy\)标记就可以了。

说难也难，说简单也简单，除了乘法加法的优先度问题之外，其他没有什么不同。

反正就是注意细节啦，因为在我区间乘法的时候忘记了更新加法的\(lazytag\)还\(WA\)了一次，所以第一要深入理解，第二要注意细节。

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,mod,t[400005],lazp[400005],lazm[400005],a[400005];
void pushup(int rt){t[rt]=(t[rt<<1]+t[rt<<1|1])%mod;}
void pushdown(int rt,int l,int r)
{
	int len=r-l+1;
	t[rt<<1]=(t[rt<<1]*lazm[rt]+lazp[rt]*(len-(len>>1)))%mod;
	t[rt<<1|1]=(t[rt<<1|1]*lazm[rt]+lazp[rt]*(len>>1))%mod;
	lazm[rt<<1]=lazm[rt]*lazm[rt<<1]%mod;
	lazm[rt<<1|1]=lazm[rt<<1|1]*lazm[rt]%mod;
	lazp[rt<<1]=(lazp[rt<<1]*lazm[rt]+lazp[rt])%mod;
	lazp[rt<<1|1]=(lazp[rt<<1|1]*lazm[rt]+lazp[rt])%mod;
	lazp[rt]=0,lazm[rt]=1;
}
void build(int rt,int l,int r)
{
	lazm[rt]=1;
	if(l==r){t[rt]=a[l]%mod;return;}
	int mid=(l+r)>>1;
	build(rt<<1,l,mid);
	build(rt<<1|1,mid+1,r);
	pushup(rt);
}
void update_plus(int rt,int l,int r,int la,int ra,int x)
{
	if(la<=l&&r<=ra)
	{
		t[rt]=(t[rt]+(r-l+1)*x)%mod;
		lazp[rt]=(lazp[rt]+x)%mod;
		return;
	}
	pushdown(rt,l,r);
	int mid=(l+r)>>1;
	if(la<=mid)update_plus(rt<<1,l,mid,la,ra,x);
	if(ra>mid)update_plus(rt<<1|1,mid+1,r,la,ra,x);
	pushup(rt);
}
void update_mul(int rt,int l,int r,int la,int ra,int x)
{
	if(la<=l&&r<=ra)
	{
		t[rt]=(t[rt]*x%mod);
		lazm[rt]=lazm[rt]*x%mod;
		lazp[rt]=lazp[rt]*x%mod;//记得更新加法的tag
		return;
	}
	pushdown(rt,l,r);
	int mid=(l+r)>>1;
	if(la<=mid)update_mul(rt<<1,l,mid,la,ra,x);
	if(ra>mid)update_mul(rt<<1|1,mid+1,r,la,ra,x);
	pushup(rt);
}
int query(int rt,int l,int r,int la,int ra)
{
	if(la<=l&&r<=ra)return t[rt]%mod;
	pushdown(rt,l,r);
	int mid=(l+r)>>1;
	int ans=0;
	if(la<=mid)ans=(ans+query(rt<<1,l,mid,la,ra))%mod;
	if(ra>mid)ans=(ans+query(rt<<1|1,mid+1,r,la,ra))%mod;
	return ans;
	
}
signed main()
{
	ios::sync_with_stdio(false);
	cin>>n>>m>>mod;
	for(int i=1;i<=n;i++)cin>>a[i];
	build(1,1,n);
	while(m--)
	{
		int opt,x,y,k;
		cin>>opt>>x>>y;
		if(opt==1)cin>>k,update_mul(1,1,n,x,y,k);
		else if(opt==2)cin>>k,update_plus(1,1,n,x,y,k);
		else cout<<query(1,1,n,x,y)<<"\n";
	}
	return 0;
}

区间最值

HDU1754 I Hate It

求区间最值的时候常常会伴随着区间更新，那么我放一道裸题。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int n,t[800005],a[800005],m;
void pushup(int rt){t[rt]=max(t[rt<<1],t[rt<<1|1]);}
void build(int rt,int l,int r)
{
	if(l==r){t[rt]=a[l];return;}
	int mid=(l+r)>>1;
	build(rt<<1,l,mid);
	build(rt<<1|1,mid+1,r);
	pushup(rt);
}
void update(int rt,int l,int r,int pos,int x)
{
	if(l==r){t[rt]=x;return;}
	int mid=(l+r)>>1;
	if(pos<=mid)update(rt<<1,l,mid,pos,x);
	else update(rt<<1|1,mid+1,r,pos,x);
	pushup(rt);
}
int query(int rt,int l,int r,int la,int ra)
{
	if(la<=l&&r<=ra)return t[rt];
	int mid=(l+r)>>1;
	int ans=0;
	if(la<=mid)ans=max(ans,query(rt<<1,l,mid,la,ra));
	if(ra>mid)ans=max(ans,query(rt<<1|1,mid+1,r,la,ra));
	return ans;
}
int main()
{
//	ios::sync_with_stdio(false);
	while(scanf("%d%d",&n,&m)!=EOF)
	{
		for(int i=1;i<=n;i++)scanf("%d",&a[i]);
		build(1,1,n);
		while(m--)
		{
			char op[2];
			int x,y;
			scanf("%s%d%d",op,&x,&y);
			if(op[0]=='U')update(1,1,n,x,y);
			else printf("%d\n",query(1,1,n,x,y));
		}		
	}

	return 0;
}

树链剖分

树链剖分是一类解决树上询问的算法。

具体来说，我们需要引入几个概念。

重儿子：每一个点的子孙中，子树最大的儿子。

轻儿子：除了重儿子之外的所有子孙。

重边：每个点和重儿子相连的那一条边。

轻边：除了重边之外的所有边。

重边相连成重链，轻链最多只有一条轻边组成。

根据这张图可以看出来，加粗的是重边，标红的是轻儿子。

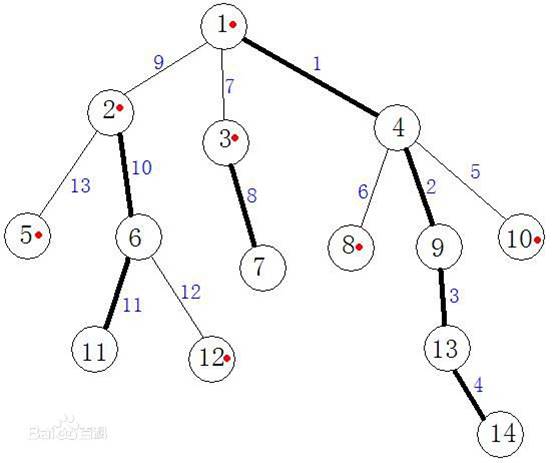
根据这样，我们就把一棵树剖成了一条一条的链，这个链的顺序可以使用\(dfs序\)来维护，树转线性过后，要维护这棵树上的各种信息，就可以使用数据结构了，我用得比较多的是线段树。

放一道题模板树链剖分

#include<bits/stdc++.h>
#define p mod
using namespace std;
int n,m,q,mod,rt,t[800005],d[200005],laz[800005],siz[100005],son[100005],top[100005],id[100005],idx,cnt,dfn[100005],fa[100005],h[200005],w[100005],wn[100005];
struct node{int v,nxt;}e[200005];
void add(int u,int v)
{
	e[++cnt].v=v;
	e[cnt].nxt=h[u];
	h[u]=cnt;
}
void dfs1(int u,int f)
{
	d[u]=d[f]+1;
	siz[u]=1;
	fa[u]=f;
	for(int i=h[u];i!=-1;i=e[i].nxt)
	{
		int v=e[i].v;
		if(v==f)continue;
		dfs1(v,u);
		siz[u]+=siz[v];
		if(siz[v]>siz[son[u]])son[u]=v;
	}
}
void dfs2(int u,int f)
{
	id[u]=++idx;
//	dfn[idx]=u;
	wn[idx]=w[u];
	top[u]=f;
	if(!son[u])return;
	dfs2(son[u],f);
	for(int i=h[u];i!=-1;i=e[i].nxt)
	{
		int v=e[i].v;
		if(v==fa[u]||v==son[u])continue;//此处的v应该和fa[u]比较！！！！！！！！ 
		dfs2(v,v);
	}
}
void pushup(int rt){t[rt]=(t[rt<<1]+t[rt<<1|1])%mod;}
void pushdown(int rt,int l,int r)
{
	if(!laz[rt])return;
	int len=r-l+1;	
	laz[rt<<1]=(laz[rt<<1]+laz[rt])%mod;
	laz[rt<<1|1]=(laz[rt<<1|1]+laz[rt])%mod;
	t[rt<<1]=(t[rt<<1]+(len-(len>>1))*laz[rt])%mod;
	t[rt<<1|1]=(t[rt<<1|1]+(len>>1)*laz[rt])%mod;
//	t[rt<<1]%=mod,t[rt<<1|1]%=mod;
	laz[rt]=0;
}
void build(int rt,int l,int r)
{
	if(l==r){t[rt]=wn[l]%mod;return;}
	int mid=(l+r)>>1;
	build(rt<<1,l,mid);
	build(rt<<1|1,mid+1,r);
	pushup(rt);
}
void update(int rt,int l,int r,int la,int ra,int x)
{
	if(la<=l&&r<=ra)
	{
		t[rt]=(t[rt]+(r-l+1)*x)%mod;
		laz[rt]=(laz[rt]+x)%mod;
		return;
	}
	pushdown(rt,l,r);
	int mid=(l+r)>>1;
	if(la<=mid)update(rt<<1,l,mid,la,ra,x);
	if(ra>mid)update(rt<<1|1,mid+1,r,la,ra,x);
	pushup(rt);
}
int query(int rt,int l,int r,int la,int ra)
{
	if(la<=l&&r<=ra)return t[rt]%mod;
	pushdown(rt,l,r);
	int ans=0;
	int mid=(l+r)>>1;
	if(la<=mid)ans=(ans+query(rt<<1,l,mid,la,ra))%mod;
	if(ra>mid)ans=(ans+query(rt<<1|1,mid+1,r,la,ra))%mod;
	return ans%mod;
}
void point_upt(int u,int v,int x)
{
	while(top[u]!=top[v])
	{
		 if(d[top[u]]<d[top[v]])swap(u,v);
		 update(1,1,n,id[top[u]],id[u],x);
		 u=fa[top[u]];
	}
	if(d[u]>d[v])swap(u,v);
	update(1,1,n,id[u],id[v],x);
}
int point_query(int u,int v)
{
	int ans=0;
	while(top[u]!=top[v])
	{
		if(d[top[u]]<d[top[v]])swap(u,v);
		ans=(ans+query(1,1,n,id[top[u]],id[u]))%mod;
		u=fa[top[u]];
	}
	if(d[u]>d[v])swap(u,v);
	ans=(ans+query(1,1,n,id[u],id[v]))%mod;
	return ans%mod;
}
void tree_upt(int rt,int x){update(1,1,n,id[rt],id[rt]+siz[rt]-1,x);}
int tree_query(int rt){return query(1,1,n,id[rt],id[rt]+siz[rt]-1)%mod;}
inline void read(int&x)
{
	x=0;char c=getchar();
	while(c<'0'||c>'9')c=getchar();
	while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
}
int main()
{
	memset(h,-1,sizeof h);
	read(n),read(m),read(rt),read(mod);
	for(int i=1;i<=n;i++)read(w[i]);
	for(int i=1,u,v;i<n;i++)read(u),read(v),add(u,v),add(v,u);
	dfs1(rt,0),dfs2(rt,rt),build(1,1,n);
	while(m--)
	{
		int opt,x,y,z;
		read(opt);
		if(opt==1)read(x),read(y),read(z),point_upt(x,y,z);
		if(opt==2)read(x),read(y),printf("%d\n",point_query(x,y));
		if(opt==3)read(x),read(y),tree_upt(x,y);
		if(opt==4)read(x),printf("%d\n",tree_query(x));
	}
	return 0;
}

Dsu on tree

\(\texttt{Dsu on tree}\)，树上启发式合并，也就是\(lxl\)口中的静态链分治。

建议去看看窝的学长的\(Blog\) pzy神仙！（破音）

考虑这样一类树上问题：

无修改操作，允许询问离线。
对子树信息进行统计。

让我们来看一道题

你看到这道题的时候是不是很懵？我也是。这道题是支持离线询问的，可以跑树上莫队，也可以跑树状数组（参照\(HH\)的项链），但作为\(dsu\)的模板题，还是要负责地讲一讲\(dsu\)。

具体做法：

定义一个全局的贡献统计\(cnt[i]\) 下标\(i\)表示这种颜色出现了多少次
利用树剖性质
遍历轻边并记录轻儿子的贡献（与此同时要记录下轻儿子点的答案）再清除轻儿子的贡献
遍历重儿子记录并且保留贡献
再次暴力统计轻儿子的贡献

那么就产生了一个困扰我非常久的问题，前后问了\(SimonSu\)，\(koalawy\)，\(pzy\)神仙，最后\(pzy\)无可奈何地给我手\(\%\)了一下，终于听懂了...

为什么我们不直接统计轻儿子再统计重儿子/先统计重儿子再统计轻儿子呢？

我们如果直接统计，那么轻/重儿子的贡献被保存在了\(cnt\)中，由于\(cnt\)的性质是全局的，所以会对我们接下来进行重/轻儿子的统计出现影响。

而为什么我们要保留重儿子而不是轻儿子呢？因为重儿子很多，轻儿子已经被证明了是不多于\(O(logn)\)条的，所以我们选择暴力统计轻儿子而不是重儿子，最终的复杂度可以证明是\(O(nlogn)\)。

\(\texttt{ p z y t x d y !!!!!!!!!!!!!!!!!}\)

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,c[200005],h[200005],cnt[200005],ans[200005],top,siz[200005],son[200005],vis[200005],num;
struct node{int v,nxt;}e[200005];
void add(int u,int v)
{
	e[++num].v=v;
	e[num].nxt=h[u];
	h[u]=num;
}
void dfs(int u,int fa)
{
	siz[u]=1;
	for(int i=h[u];i!=-1;i=e[i].nxt)
	{
		int v=e[i].v;
		if(v==fa)continue;
		dfs(v,u);
		siz[u]+=siz[v];
		if(siz[v]>siz[son[u]])son[u]=v;
	}
}
void calc(int u,int fa,int val)
{
	if(val>0)
	{
		if(!cnt[c[u]])top++;
		cnt[c[u]]++;
	}
	else
	{
		if(cnt[c[u]]<=1)top--;
		cnt[c[u]]--;
	}
	for(int i=h[u];i!=-1;i=e[i].nxt)
	{
		int v=e[i].v;
		if(v==fa||vis[v])continue;
		calc(v,u,val);
	}
}
void dsu(int u,int fa,int val)
{
	for(int i=h[u];i!=-1;i=e[i].nxt)
	{
		int v=e[i].v;
		if(v==fa||v==son[u])continue;
		dsu(v,u,0);
	}
	if(son[u])dsu(son[u],u,1),vis[son[u]]=1;//当我们遍历了全部的轻儿子 如果有一个重儿子没有被遍历 就遍历qwq
	calc(u,fa,1),vis[son[u]]=0; //累计答案
	ans[u]=top;//答案下传
	if(!val)calc(u,fa,-1);//如果当前节点是轻儿子 那么我们需要减去答案 
	
}
inline void read(int&x)
{
	x=0;char c=getchar();
	while(c<'0'||c>'9')c=getchar();
	while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
}
int main()
{
	memset(h,-1,sizeof h);
	read(n);
	for(int i=1,u,v;i<n;i++)read(u),read(v),add(u,v),add(v,u);
	for(int i=1;i<=n;i++)read(c[i]);
	dfs(1,0),dsu(1,0,1);
	read(m);
	for(int i=1,ask;i<=m;i++)read(ask),printf("%d\n",ans[ask]);
	return 0;
}

posted @ 2019-11-07 17:03 haruka酱阅读(568) 评论(4) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

初次见面，我是haruka。

或许是不知梦的缘故，流离之人追逐幻影。