数据挖掘 | 数据隐私（4） | 差分隐私 | 差分隐私概论（下）（Intro to Differential Privacy 2）

L4-Intro to Differential Privacy

拉普拉斯机制（Laplace Mechanism）

上一节课中，我们讨论了随机响应，这是一种适合于单个位的隐私化。这种算法一般来说并不直接也误差较大。今日所关注的是拉普拉斯机制，可以直接应用于任意一种类型的数字查询。在引入拉普拉斯机制，首先提出一个概念：函数敏感度（sensitivity），一般特指L1敏感度（即基于L1范数的敏感度），定义如下：

定义1

使\(f:\mathcal{X}^n\rightarrow\mathbb{R} ^k\)，那么\(f\)的\(\mathcal{l_1}\)-敏感度为：

\[\Delta^{(f)}=\max_{X,X'}||f(X)-f(X')||_1 \]

其中\(X\)和\(X'\)为邻近数据集

后面丢掉\(f\)，只使用\(\Delta\)以表示\(\mathcal{l_1}\)-敏感度。

敏感度用于衡量差分隐私的内容是合适而自然的，正因为差分隐私试图掩盖一个个个体的具体分布差距，通过这一敏感度作为上界，就可以衡量该函数应该会发生多大的改变。值得注意的是，我们用的是\(\mathcal{l_1}\)-敏感度，而非\(\mathcal{l_2}\)-敏感度，但是在其他分布例如说高斯机制中会使用。举个例子：\(f=\frac{1}{n}\sum^n_{i=1}X_i \ \ X_i\in\{0,1\}\)，很容易算出敏感度为\(1/n\)，因为只有一个位被翻转。

定义2

对于位置与规模参数分别为\(0\)与\(b\)的拉普拉斯分布，如下定义其密度函数：

\[p(x)=\frac{1}{2b}\exp(-\frac{|x|}{b}) \]

注意到拉普拉斯分布的方差为\(2b^2\)。

如下图所示，拉普拉斯分布本质是两个对称的指数分布，在\(x\in [0,\infty)\)存在正比于\(exp(-cx)\)的密度函数，而拉普拉斯分布则是在\(x\in \mathbb{R}\)存在正比于\(\exp(-c|x|)\)的密度函数。另外高斯分布的尾部要比拉普拉斯分布的稍轻一点，换句话来说就是高斯分布的中心化程度更高。

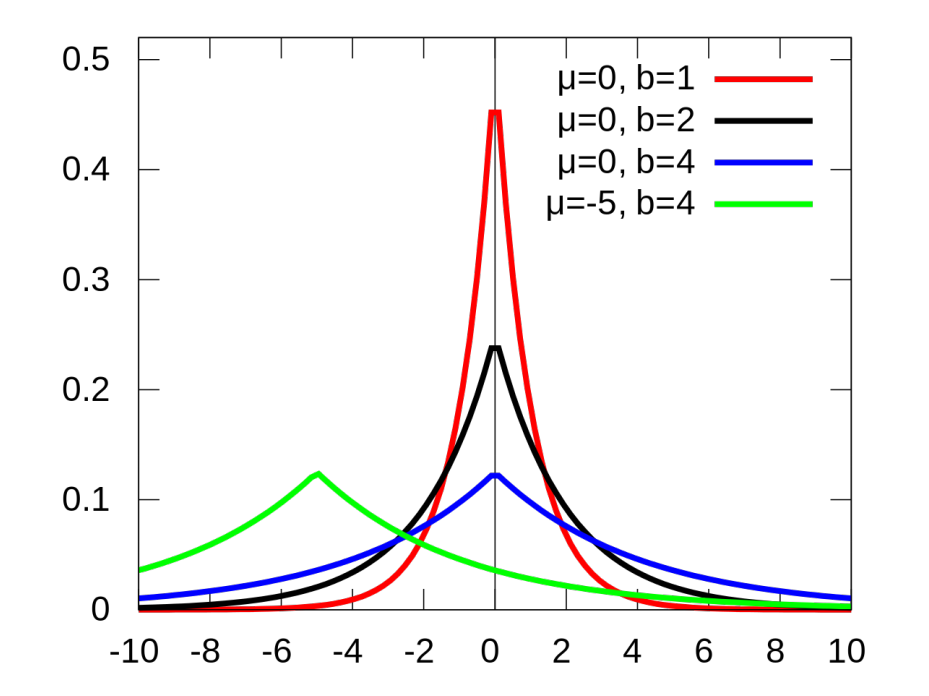
介绍了拉普拉斯分布之后，就可以引入拉普拉斯机制这一概念，原理非常简单：即是按照数据敏感度的程度添加噪音。

定义3

使\(f:\mathcal{X}^n\rightarrow \mathbb{R} ^k\)，那么拉普拉斯机制即是

\[M(X)=f(X)+(Y_1,\dots,Y_k) \]

其中\(Y_i\)是独立的拉普拉斯分布，\(Laplace(\Delta/\epsilon)\)的随机变量。

由此我们就可以将其应用于例子中的\(f=\frac{1}{n}\sum^n_{i=1}X_i\)，并且\(k=1\)。那么\(\Delta = 1/n\)。为此，对其施加拉普拉机制之后得到\(\tilde p=f(X)+Y\)，其中\(Y\)为\(Laplace(1/(\epsilon n))\)。由定义可知，\(\mathbf{E}[\tilde p]=p\)，\(\mathbf{Var}[\tilde p]=\mathbf{Var}[Y]=O(1/(\epsilon^2 n^2))\)，然后通过切比雪夫不等式就可以得到合理概率界限。对比于\(\epsilon\)-随机响应的精确度\(O(1/(\epsilon\sqrt n))\)，可见拉普拉斯机制是二次的，小于\(\epsilon\)-随机响应。

定理4

拉普拉斯机制乃是\(\epsilon\)-差分隐私

证明：假若\(X\)与\(Y\)为一对邻近数据集，存在一个数据条目不一致。使得\(p_X(z)\)与\(p_Y(z)\)为点\(z\in\mathbb{R}^k\)的概率密度函数\(M(X)\)与\(M(Y)\)。为此我们需要证明其上界为\(\exp(\epsilon)\)，那么对于任意一个\(X\)与\(Y\)的\(z\)

\[\begin{align} \frac{p_X(z)}{p_Y(z)} & = \frac{\prod^k_{i=1}\exp(-\frac{\epsilon|f(X)_i-z_i|}{\Delta})} {\prod^k_{i=1}\exp(-\frac{\epsilon|f(Y)_i-z_i|}{\Delta})} \\ & = \prod^k_{i=1}\exp(-\frac{\epsilon(|f(X)_i-z_i|-|f(X)_i-z_i|)}{\Delta}) \\ & \le \prod^k_{i=1}\exp(-\frac{\epsilon|f(X)_i-f(X)_i|}{\Delta}) \\ & = \exp(\frac{\epsilon\sum^k_{i=1}|f(X)_i-f(X)_i|}{\Delta}) \\ & = \exp(\frac{\epsilon||f(X)-f(X)||_1}{\Delta}) \\ & \le \exp(\epsilon) \end{align} \]

首先应用三角不等式，然后应用\(\mathcal{l_1}\)-敏感度的定义。

计数查询（Counting Queries）

现在要讨论计数查询的情况了，计数查询也能用非标准化版本的差分隐私来称呼。

首先假若每个个体都拥有一个隐私为\(X_i\in\{0,1\}\)，其中定义\(f\)为最终他们的求和。那么敏感度为\(1\)，经过\(\epsilon\)-差分隐私的数据就是\(f(X)+\text{Laplace}(1/\epsilon)\)。其误差则为\(O(1/\epsilon)\)，独立于数据集的规模。

现在我们考虑多次查询。假若我们拥有\(k\)次查询\(f=(f_1,\dots,f_k)\)，都是提前指定好的。最后就会输出一个向量\(f(X) + Y\)，其中\(Y_i\)都符合i.i.d条件的拉普拉斯随机变量。现在我们再考虑这个分布的规模系数。对于每个具体的查询\(f_j\)都拥有敏感度 \(1\)，但是又要考虑所有查询都是基于一个数据集，也就是说单个查询的改变会影响到多种查询组合。例如说，交换两个个体，二者的位是相反的，那么所有查询都会改变\(1\)，因此最终的\(\mathcal{l_1}\)-敏感度为\(k\)。我们再采用数学的方法进行证明：由于\(f(X)=\sum(f_1(X_i\dots,f_k(X_i))\)，而临近数据集\(X\)与\(Y\)之间差别在于\(x\)与\(y\)，为此\(\mathcal{l_1}\)差分为\(\sum_j|f_j(x)-f_j(y)|\)，然后上界可以算出来得到\(\sum_j|f_j(x)-f_j(y)|\le \sum_j 1=k\)。

算出来其敏感度上界\(\Delta=1\)，也就得到了噪音\(Y_i\sim\text{Laplace}(k/\epsilon)\)，然后添加到每个坐标分量上面，每次计数查询都带上了总规模为\(O(k/\epsilon)\)的误差。

有些地方还是必须注意：第一点，这种处理\(k\)计数查询的方法只适用于提前指定好的查询，也就是说非适应性的查询。第二点，对于 Dinur-Nissim攻击，其中数据分析器进行\(\Omega(n)\)次技术查询，那么管理器带了总量为\(O(\sqrt n)\)的噪音，那么数据分析器

就能重构数据集并且使得其符合\(BNP\)性。而完美采用的策略使得数据分析器查询\(O(n)\)时，加入了\(O(n/\epsilon)\)的噪音，成功保护了隐私。今后还要讨论如何面对更为强大的攻击，以及如何在减少噪音的情况下隐私性不变。

直方图（Histograms）

这里提出一种新的查询方法为直方图查询（histogram query），相比于比较悲观的计数查询（因为计数查询一个改变会影响整个结果），某些特定的数据结构可以让我们的数据查询得到更好的敏感度。这里我们举个带有明确特征的例子：例如说人的年龄（注意是通过向下取整得到离散的数值）。其实类似于计数查询，每个人都只有一个年龄，而我们的查询具体就是“有多少个人其年龄为\(X\)”。函数\(f\)定义为\((f_0,f_1,\dots,f_{k-1})\)，其中\(k_i\)就是查询有多少人为\(i\)岁，显然这个函数的\(\mathcal{l_1}\)-敏感度为\(2\)，因为改变其中一个人的岁数会导致一个年龄桶总数的下降，另一个年龄桶总数的上升。基于上述内容，拉普拉斯机制的处理方法即是输出\(f(X)+Y\)，其中\(Y_i\sim\text{Laplace}(2/\epsilon)\)，最终加入的噪音总量则为桶的总量\(k\)

公理5.

对于\(Y\sim\text{Laplace}(b)\)，有：

\[\mathbf{Pr}[|Y|\ge tb]=\exp(-t) \]

那么对于第\(i\)个桶，其误差显而易见为\(Y_i\)并且符合\(\mathbf{Pr}[|Y_i|\ge2\log(k/\beta)/\epsilon]\le\beta/k\)，可以证得对于任意一个桶都有误差\(\ge2\log(k/\beta)/\epsilon\)对于大多数\(\beta\)的取值。换一种说法来说，就是直方图查询的误差是对数复杂度，而计数查询为线性复杂度的误差。

差分隐私的性质（Properties of Differential Privacy）

后处理性（Post-Processing）

只要数据不再被使用，那么经过隐私化的数据将不能再被去隐私化。

定理6.

使\(M:X^n\rightarrow Y\)为\(\epsilon\)-DP算法，以及\(F:Y\rightarrow Z\)为一个随机映射。那么对于\(F\cdot M\)也是\(\epsilon\)-DP。

证明：

\[\begin{align} \mathbf{Pr}[F(M(X))\in T] & = \mathbf{E}_{f\sim F}[\mathbf{Pr}[M(X)\in f^{-1}(M)]] \\ & \le\mathbf{E}_{f\sim F}[e^{\epsilon}\mathbf{Pr}[M(X')\in f^{-1}(M)]] \\ & = e^{\epsilon}\mathbf{Pr}[F(M(X'))\in T] \end{align} \]

群组隐私（Group Privacy）

定理7.

使\(M:X^n\rightarrow Y\)为\(\epsilon\)-DP算法。其中\(X\)与\(X'\)为在\(k\)个位置不一致的邻近数据集。那么对于所有\(T\subseteq Y\)，满足：

\[\begin{align} \mathbf{Pr}[M(X)\in T] & \le \exp(k\epsilon)\mathbf{Pr}[M(X')\in T] \end{align} \]

证明：先使\(X^{(0)}=X\)，\(X^{(k)}=X'\)，其中二者在\(k\)位置存在差异。那么存在一系列从\(X^{(0)}\)到\(X^{(k)}\)的连续邻近数据集对。那么对于所有\(T\subseteq Y\)，满足：

\[\begin{align} \mathbf{Pr}[M(X^{(0)})\in T] & \le e^\epsilon \mathbf{Pr}[M(X^{(1)})\in T] \\ & \le e^{2\epsilon} \mathbf{Pr}[M(X^{(2)})\in T] \\ & \cdots\\ & \le e^{k\epsilon} \mathbf{Pr}[M(X^{(k)})\in T] \\ \end{align} \]

基本组合性（ (Basic) Composition ）

对于\(M=(M_1,\dots,M_k)\)，为一系列\(k\)个\(\epsilon\)-DP算法，其输出为\(y=(y_1,\dots,y_k)\)，那么满足：

\[\begin{align} \frac{\mathbf{Pr}[M(X)=y]}{\mathbf{Pr}[M(X')=y]} & = \prod^k_{i=1}\frac{\mathbf{Pr}[M_i(X)=y_i|(M_1(X),\dots,M_{i-1}(X))=(y_1,\dots,y_k)]} {\mathbf{Pr}[M_i(X')=y_i|(M_1(X'),\dots,M_{i-1}(X'))=(y_1,\dots,y_k)]} \\ & \le \prod^k_{i=1} \exp(\epsilon) \\ & = \exp(k\epsilon) \end{align} \]