arxiv：多元时间序列推断的深度学习：一项调查

代码地址：https://github.com/wenjiedu/awesome_imputation?tab=readme-ov-file
摘要
普遍存在的缺失值导致多元时间序列数据被部分观测到，破坏了时间序列的完整性，阻碍了有效的时间序列数据分析。最近，深度学习插补方法在提高损坏的时间序列数据的质量方面取得了显著成功，从而提高了下游任务的性能。本文对最近提出的深度学习插补方法进行了全面的调查。首先，我们为所审查的方法提出了一个分类法，然后通过突出这些方法的优点和局限性，对这些方法进行了结构化的审查。

我们还进行了实证实验，研究了不同的方法，并比较了它们对下游任务的增强效果。最后，指出了未来多元时间序列插补研究的未决问题。本工作的所有代码和配置，包括定期维护的多元时间序列插补论文列表

1简介
在金融[Bai and Ng， 2008]、医学[Esteban et al .， 2017]、交通运输[Gong et al .， 2021]等多个领域，多变量时间序列的数据收集过程往往充满困难和不确定性，如传感器故障、系统环境不稳定、隐私问题或其他原因。这导致数据集通常包含大量缺失值，并会严重影响下游分析和决策的准确性和可靠性。例如，现实世界的公共医疗时间序列数据集PhysioNet2012 [Silva等人，2012]的平均缺失率甚至超过80%，这使得分析具有挑战性。因此，探索如何合理有效地对多元时间序列数据中的缺失分量进行归因是非常必要的。

方法是用统计数据（如零值、平均值和最后观测值[Amiri和Jensen， 2016]）或简单统计模型（包括ARIMA [Bartholomew， 1971]、ARFIMA [Hamzac ehbi， 2008]和SARIMA [Hamzac ehbi， 2008]）替代缺失值。此外，回归、k近邻、矩阵分解等机器学习技术在解决多元时间序列中缺失值的文献中获得了突出的地位。这些方法的关键实现包括KNNI [Altman， 1992]、TIDER [Liu et al ., 2022]、MICE [Van Buuren and Groothuis-Oudshoorn， 2011]等。

虽然统计和机器学习方法简单有效，但它们在捕捉时间序列数据中固有的复杂时间关系和复杂变化模式方面存在不足，导致性能有限。近年来，深度学习方法在缺失数据的输入方面表现出了很强的建模能力。

这些方法利用强大的深度学习模型，如transformer、变分自动编码器（VAEs）、生成对抗网络（GANs）和扩散模型来捕捉时间序列的内在属性和潜在的复杂动态。这样，深度学习插值方法就可以从观测到的数据中学习到真实的底层数据分布，从而为缺失的分量预测出更可靠合理的值。我们注意到有几个相关的调查[Khayati等人，2020；Fang和Wang， 2020]，主要关注统计和机器学习的imputation方法，但他们只对深度学习的imputation方法进行了有限的考虑。

多元时间序列归算是后续时间序列分析的关键数据预处理步骤，深入系统地研究深度多元时间序列归算方法将对时间序列领域的发展起到重要的推动作用。

在本文中，我们通过提供多元时间序列imputation （MTSI）的深度学习方法的最新发展的全面总结，努力弥合现有的知识差距。首先，我们简要介绍了该主题，然后提出了一种新的分类法，基于两个角度的分类方法：归算不确定性和神经网络结构。输入不确定性反映了对缺失数据输入值的置信度，捕获这种不确定性涉及随机生成样本并基于这些不同的样本[Little和Rubin， 2019]。因此，我们将代入方法分为预测方法和生成方法，前者提供固定估计，后者提供可能值的分布，以解释代入的不确定性。对于神经网络架构，我们探索了一系列为MTSI量身定制的深度学习模型，包括基于循环神经网络（RNN）的模型、基于图神经网络（GNN）的模型、基于卷积神经网络（CNN）的模型、基于注意力的模型、基于变分自编码器（VAE）的模型、基于生成对抗网络（GAN）的模型和基于扩散的模型。为了在真实场景中提供实用的归算指南，我们进行了广泛的实证研究，研究了深度多元时间序列归算模型的多个方面，包括归算性能和对下游任务（如分类）的改进。据我们所知，这是MSTI领域深度学习算法的第一次全面和系统的回顾，旨在促进该领域的进一步研究。在我们的GitHub存储库中可以找到不断更新的相应资源1。

综上所述，本文的贡献包括：1)考虑了输入不确定性和神经网络结构的深度多元时间序列输入方法的新分类，并对方法进行了全面的回顾；2)通过我们开发的PyPOTS工具包对imputation算法进行彻底的实证评估；3) MTSI未来研究机会的探索。
2 预测方法
2.1
预测估算方法始终预测相同缺失成分的确定性值，从而不考虑估算值中的不确定性。通常，这些方法采用基于重构的学习方式，其学习目标为：

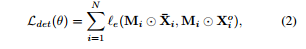
其中，e是绝对误差或平方误差函数。
2.2 基于 RNN 的模型
作为一种自然的序列数据建模方法，递归神经网络（RNNs）很早就在高级时间序列分析的主题上得到了发展，而代入也不例外。GRU- d [Che et al .2018]是GRU的一个变体，用于处理包含缺失值的时间序列。它是由时间衰减机制调节的，该机制以时间矩阵δi为输入，对缺失值引起的时间不规则性进行建模。时间信念记忆[Kim和Chi，2018]受到称为霍奇金-赫胥黎模型的生物神经模型的启发，提出通过使用双向RNN计算每个特征最后一次观察的信念并根据其信念输入缺失值来处理缺失数据。M-RNN [Yoon等人，2019]是以多向方式工作的RNN变体。该模型使用双向RNN模型在数据流内进行插值，并使用完全连接的网络跨数据流进行插值。BRITS [Cao等人，2018]使用双向RNN对不完全时间序列进行建模。它将缺失值作为RNN图的变量，并用RNN的隐藏状态填充缺失数据。除了imputation之外，BRITS还能够同时处理时间序列分类任务。M-RNN和british都采用GRU-D的时间衰减函数来捕捉信息缺失，从而提高性能。后续作品，如[Luo et al.2018；Luo等人，2019；Liu et al.2019；Miao等人，2021]将rnn与GAN结构相结合，以更高的精度输出imputation。

2.3 基于 CNN 的模型
卷积神经网络（cnn）代表了一种基础的深度学习架构，广泛应用于复杂的时间序列分析。TimesNet [Wu et al .， 2023a]创新性地采用快速傅立叶变换将一维时间序列重构为二维格式，便于利用cnn进行数据处理。同样在GP-VAE [Fortuin et al .， 2020]中，cnn在编码器和解码器中都扮演主干的角色。此外，cnn在基于注意力的模型（如DeepMVI [Bansal等人，2021]）以及基于扩散的模型（如CSDI [Tashiro等人，2021]）中作为关键的特征提取器，通过将输入数据映射到嵌入空间中进行后续处理。

2.4
基于gnn的模型，将时间序列视为图序列，使用学习到的节点表示重建缺失值。[Cini等人，2022]的作者介绍了GRIN，这是MTSI的第一个基于图的循环架构。GRIN利用双向图递归神经网络有效地利用时间动态和空间相似性，从而显著提高了imputation精度。此外，还开发了SPIN [Marisca等，2022]，将一种独特的稀疏时空注意机制整合到GNN框架中。该机制明显克服了GRIN的错误传播问题，并增强了对高度缺失数据所带来的数据稀疏性的鲁棒性
2.5
基于注意力的模型
自从 Transformer 在 [Vaswani et al, 2017] 中提出以来，自注意力机制已被广泛用于建模包括时间序列在内的序列数据 [Wen et al, 2023]。
CDSA [Ma et al, 2019] 提出通过联合学习时间、位置和测量来估算地理标记的时空数据。 DeepMVI [Bansal et al, 2021] 将转换器与卷积技术集成，定制关键查询设计以有效解决缺失值插补问题。对于每个时间序列，DeepMVI 利用注意力机制同时提取长期季节性、细粒度局部和跨维度嵌入，将它们连接起来以预测最终输出。 NRTSI [Shan et al, 2023] 直接利用 Transformer 编码器进行建模，并将时间序列数据作为一组时间戳和测量元组。作为一个排列模型，该模型必须在时间维度上进行迭代来处理时间序列。 SAITS [Du et al, 2023] 采用自监督训练方案来处理缺失数据，该方案集成了双重联合学习任务：掩蔽插补任务和观察重建任务。该方法具有两个对角屏蔽自注意力块和一个加权组合块，利用注意力权重和缺失指标来提高插补精度。除了上述模型之外，注意力机制还被广泛应用于在扩散模型中构建去噪网络，例如 CSDI [Tashiro et al, 2021]、MIDM [Wang et al, 2023]、PriSTI [Liu et al, 2023]、 ETC。
2.6 优点和缺点
本小节综合了所讨论的预测插补方法的优点和挑战。基于 RNN 的模型虽然擅长捕获顺序信息，但本质上受到其顺序处理性质和内存限制的限制，这可能会导致长序列的可扩展性问题 [Khayati et al, 2020]。尽管 CNN 已经发展了数十年，并且是捕获邻域信息和局部连通性的有用特征提取器，但它们的内核大小和工作机制本质上限制了它们作为骨干的时间序列数据的性能。由于注意力机制，基于注意力的模型通常在插补任务中优于基于 RNN 和 CNN 的方法，因为它们具有处理远程依赖性和并行处理能力的卓越能力。基于 GNN 的方法提供了对时空动力学的更深入的理解，但它们通常会增加计算复杂性，给大规模或高维数据带来挑战。
**3 生成方法 **
在本节中，我们研究生成插补方法，包括三种主要类型：基于 VAE、基于 GAN 和基于扩散的模型。
3.1 学习目标 生成方法本质上是建立在 VAE、GAN 和扩散模型等生成模型的基础上的。它们的特点是能够为缺失的观测值生成不同的输出，从而能够量化插补不确定性。通常，这些方法从观察到的数据中学习概率分布，然后为缺失的观察生成与这些学习到的分布略有不同的值。因此，生成方法的主要学习目标被定义为

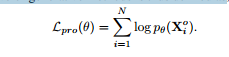
式中，θ为输入模型M
3.2 基于 VAE 的模型
VAEs采用编码器-解码器结构，通过最大化边际似然的证据下界（ELBO）来近似真实数据分布。在[Fortuin等人，2020]中，作者提出了第一种基于vae的imputation方法GP-VAE，他们在潜在空间中使用高斯过程来捕获时间动态。此外，GP-VAE的ELBO仅根据观测到的数据特征进行评估。[Mulyadi等人，2021]的作者设计了V-RIN，以减轻缺失价值估算中有偏差估计的风险。V-RIN通过适应模型输出上的高斯分布来捕获不确定性，特别是将来自VAE模型的重构数据的方差解释为不确定性度量。然后，它对时间动态进行建模，并通过不确定性感知GRU将这种不确定性无缝集成到输入数据中。最近，[Kim等人，2023]的作者提出了supnotMIWAE，并引入了一个额外的分类器，他们扩展了GP-VAE中的ELBO，以模拟观测数据、掩模矩阵和标签的联合分布。通过这种方式，他们的ELBO有效地建模了输入不确定性，并且额外的分类器鼓励VAE模型产生对下游分类任务更有利的缺失值
3.3 基于 GAN 的模型 GAN 通过两个组件之间的极小极大博弈促进对抗性训练：一个旨在模仿真实数据分布的生成器，以及一个负责区分生成数据和真实数据的鉴别器。这种动态促进了合成数据的逐步细化，使其越来越类似于真实样本。在 [Luo et al, 2018] 中，作者提出了一种两阶段 GAN 插补方法（GRUI-GAN），这是第一个基于 GAN 的时间序列数据插补方法。 GRUI-GAN首先通过标准的对抗训练方式学习观测到的多元时间序列数据的分布，然后优化生成器的输入噪声，以进一步最大化生成的和观测到的多元时间序列数据的相似度。然而，GRUI-GAN 的第二阶段需要大量时间来找到最佳匹配的输入向量，并且该向量并不总是最好的，特别是当“噪声”的初始值设置不正确时。然后，进一步提出了一种端到端的 GAN 插补模型 E2GAN [Luo et al, 2019]，其中生成器采用去噪自动编码器模块来避免 GRUIGAN 中的“噪声”优化阶段。同时，[Liu et al, 2019] 中的作者提出了一种非自回归多分辨率 GAN 模型（NAOMI），其中生成器由前向-后向编码器和多分辨率解码器组装而成。插补数据由多分辨率解码器以非自回归方式递归生成，这减轻了涉及高缺失和长序列时间序列数据的场景中的错误积累。另一方面，在 [Miao et al, 2021] 中，作者提出了 USGAN，它通过将鉴别器与时间提醒矩阵集成来生成高质量的估算数据。该矩阵增加了鉴别器训练的复杂性，从而提高了生成器的性能。此外，他们通过引入额外的分类器，将 USGAN 扩展为半监督模型 SSGAN。通过这种方式，SSGAN 利用标签信息，使得生成器可以同时根据观察到的成分和数据标签来估计缺失值。
3.4 基于扩散的模型
作为新兴且有效的生成模型类别，扩散模型擅长通过扩散步骤的马尔可夫链逐步添加然后反转噪声来捕获复杂的数据分布。与 VAE 不同，这些模型利用固定的训练程序，并使用保留输入数据维度的高维潜在变量进行操作。[Tashiro et al, 2021] 中引入的 CSDI 是专为 MTSI 设计的开创性扩散模型。与传统的扩散模型不同，CSDI采用条件训练方法，其中观测数据的子集被用作条件信息，以促进剩余观测数据片段的生成。然而，CSDI 中的去噪网络依赖于两个变压器，在变量数量和时间序列长度方面表现出二次复杂度。这种设计限制引起了对内存限制的担忧，特别是在对广泛的多元时间序列进行建模时。为了应对这一挑战，[Alcaraz 和 Strodthoff，2023] 的后续工作引入了 SSSD，它通过用结构化状态空间模型替换 Transformer 来解决二次复杂度问题 [Gu et al, 2022]。这种修改被证明是有利的，特别是在处理冗长的多元时间序列时，因为它减轻了内存溢出的风险。[Chen et al, 2023] 中引入的另一种方法 CSBI 通过将扩散过程建模为薛定谔桥问题来提高效率，该问题可以转换为计算友好的随机微分方程。
此外，扩散模型的有效性显着受到条件信息的构建和利用的影响。 MIDM [Wang et al, 2023] 提出从去噪过程中观测数据表示条件的分布中采样噪声，通过这种方式，它可以明确保留观测数据和缺失数据之间的内在相关性。 PriSTI [Liu et al, 2023]引入时空依赖性作为条件信息，即为去噪网络提供通过时空插补的条件特征计算出的时空注意力权重。此外，DA-TASWDM [Xu et al, 2023] 建议纳入动态时间关系，即不同的采样密度进入去噪网络以进行医学时间序列插补。与上述将时间序列视为离散时间步长的基于扩散的方法相比，SPD [Bilosˇ et al, 2023]将时间序列视为底层连续函数的离散实现，并使用随机过程扩散生成用于插补的数据。这样，SPD将连续噪声过程假设为不规则时间序列的归纳偏差，从而更好地捕捉真实的生成过程，尤其是数据固有的随机性。
3.5 优点和缺点
本小节描述了上述生成插补模型的优点和局限性。基于 VAE 的模型擅长显式地建模概率，并为理解数据分布提供理论基础。然而，它们通常受到生成能力的限制，这可能会限制它们捕获复杂数据可变性的性能。另一方面，基于 GAN 的模型在数据生成方面表现出色，能够提供高质量的插补，并且对原始数据分布的保真度令人印象深刻。然而，由于梯度消失等问题，它们的训练非常具有挑战性[Wu et al, 2023b]，这可能会阻碍模型的稳定性和收敛性。基于扩散的模型成为强大的生成工具，具有捕获复杂数据模式的强大能力。然而，它们的计算复杂性相当大，并且还遇到与缺失部分和观察到的部分之间的边界一致性相关的问题[Lugmayr et al, 2022]。
**4 **
时间序列插补工具包在时间序列插补任务上，现有的库提供了朴素的处理方式、统计方法、机器学习插补算法和深度学习插补神经网络，以方便使用。
imputeTS [Moritz 和 Bartz-Beielstein, ]，R 中的一个库，提供了几种简单的方法（例如平均值、最后观察结转等）和常用的插补算法（例如线性插值、卡尔曼平滑和加权移动）平均值）但仅适用于单变量时间序列。另一个著名的 R 包，mice [Van Buuren 和 Groothuis-Oudshoorn，2011]，通过链式方程实现了称为多元插补的方法来解决数据缺失问题。尽管它不是专门针对时间序列的，但它在实践中广泛用于多元时间序列插补，特别是在统计领域。 Impyute2 和 Autoimpute3 都为横截面数据和时间序列数据提供朴素插补方法。 Impyute 仅使用移动平均窗口等简单方法，而 Autoimpute 集成了参数方法，例如多项式插值和样条插值。
最近，GluonTS [Alexandrov et al, 2020]，一种时间序列的生成机器学习包，提供了一些简单的方法，例如虚拟值插补和随意平均值插补，来处理缺失值。除了简单的非参数方法之外，Sktime [Loning ¡ et al, 2019] 还实现了另一种选项，允许用户利用集成的机器学习插补算法来拟合和预测给定数据中的缺失值，尽管这适用于单变量方式。在深度学习插补方面，PyPOTS [Du, 2023] 是一个专注于对部分观察的时间序列进行端到端建模的工具箱。它包含十多个用于不完整时间序列任务的深度学习神经网络，到目前为止包括八个插补模型。
**5 **
实验评估和讨论在本节中，通过实证实验来评估和分析不同类别的深度多元时间序列插补方法。结果是在配备 AMD EPYC 7543 32 核 CPU 和 NVIDIA GeForce RTX 4090 GPU 的机器上获得的。所有代码，包括数据预处理脚本、模型配置和训练脚本，都可以在 GitHub 存储库 https://github.com/WenjieDu/Awesome Imputation 中公开获取。
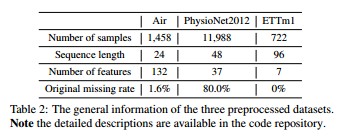
5.1 数据集和插补方法具体而言，在三个真实世界数据集（Air [Zhang et al, 2017]、PhysioNet2012 [Silva et al, 2012] 和 ETTm1 [Zhou et al] 上测试了三种朴素插补方法和八个深度学习神经网络al, 2021] 表 2），这些都是文献中常用的。
在插补方法方面，除了以 Mean、Median 和 LOCF（最后观察结转）三种朴素方式作为基线外，还从不同类别中选择了以下八种代表性深度学习模型进行实验研究：M-RNN [Yoon et al, 2019]、GP-VAE [Fortuin 等人，2020]、BRITS [Cao 等人，2018]、USGAN [Miao 等人，2021]、 CSDI [Tashiro 等人，2021]、TimesNet [Wu 等人，2023a]、Transformer [Du 等人，2023] 和 SAITS [Du 等人，2023]。实验是使用 PyPOTS4 [Du, 2023] 进行的，所有上述插补方法都可以在工具箱中立即使用。此外，为了公平比较，所有深度学习方法的超参数都通过 PyPOTS 中的调整功能进行了优化。

5.2 结果和分析 插补精度评估
表 3 显示了三个数据集的 12 种方法的误差度量 MAE（平均绝对误差）和 MSE（均方误差）的插补结果。这些数字表明这些方法的性能在不同的数据集上有所不同这项研究中没有明显的赢家。需要做进一步的工作来深入比较预测和生成插补方法。值得注意的是，在 Air 和 ETTm1 数据集等数据由传感器连续记录且缺失比例相对较低的情况下，非参数 LOCF 方法表现出了值得称赞的性能。相反，在缺失率较高的 PhysioNet2012 数据集中，深度学习插补方法明显优于统计方法。这一观察结果证实了深度学习方法有效捕获复杂时间动态并准确学习数据分布的能力，特别是在高度稀疏、离散观察的场景中。
下游任务评估通常，插补值的质量越好代表插补后数据集的整体质量越好。因此，除了插补性能比较之外，文献中还有一个实验设置，从下游任务性能的角度评估方法[Du et al, 2023]。
这项工作也采用了这样的研究，以帮助评估所选方法。一个简单的 LSTM 模型在 PhysioNet2012 数据集上执行二元分类任务，其中每个样本都有一个标签，指示 ICU 中的患者是否死亡。 PhysioNet2012数据集通过插补方法进行处理，结果如表3所示。选择PR-AUC（精确回忆曲线下面积）和ROC-AUC（受试者工作特征曲线下面积）作为指标，考虑到数据集有不平衡的类别和 14.2% 的正样本。请注意，此实验中唯一的变量是估算数据。
如表 4 所示，分类器可以受益于对下游分类任务的更好的插补。 SAITS 插补的最佳结果分别比 PRAUC 和 ROC-AUC 指标上的最佳朴素插补平均值分别获得 5% 和 1% 的增益。请注意，这种改进只是通过更好的插补来实现的，这可以看作是本实验中的数据预处理步骤。此外，这提出了一个研究问题，即如何使深度学习插补模型从插补任务和下游任务中学习，以从不完整的时间序列中获得一致且统一的表示。
复杂性分析 我们在表 5 中总结了深度学习插补模型的时间和内存复杂性。
另外，还列出了它们在Phy-sioNet2012测试集上的实际推理时间，以便清楚比较。

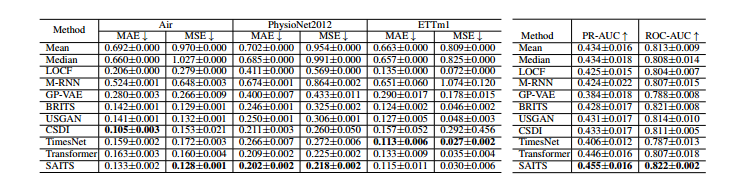
表3:Air、PhysioNet2012和ETTm1数据集上估算方法的MAE和MSE比较。报告值为五组的平均值±标准差 表4：五次运行的分类结果均值和标准差。

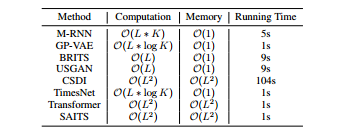
表5：在PhysioNet2012测试集上，输入模型的计算复杂度和空间复杂度，以及运行时间（秒）
6 结论和未来方向
本文对专门为多元时间序列插补量身定制的深度学习模型进行了系统回顾。我们引入了一种新颖的分类法对所审查的方法进行分类，对每种方法进行了全面的介绍和实验比较。为了推动这一领域的发展，本文最后确定并讨论了以下未来研究的潜在途径。
缺失模式现有的插补算法主要在 MCAR 或 MAR 下运行。然而，现实世界的缺失数据机制通常更加复杂，MNAR 数据普遍存在于物联网设备 [Li 等人，2023]、临床研究 [Ibrahim 等人，2012] 和气象学 [Ruiz 等人] 等不同领域。 ，2023]。 MNAR 的不可忽视性质表明观测数据和真实数据之间存在分布变化 [Kyono et al, 2021]。例如，在气流信号分析中 [Ruiz et al, 2023]，缺乏高值观测会导致 MNAR 缺失机制并导致峰值饱和，与真实的基础数据分布相比，观测到的数据分布明显偏斜。此场景说明了插补方法如何可能在模型参数估计中产生归纳偏差，并在 MNAR 存在的情况下表现不佳。与 MCAR 和 MAR 不同，解决 MNAR 环境中的缺失数据需要创新方法来实现更好的性能。
下游性能 估算缺失值的主要目标在于增强下游数据分析，特别是在信息不完整的情况下。普遍的方法是“估算和预测”两阶段范式，其中缺失值估算是数据预处理的一部分，然后是串联或顺序的特定于任务的下游模型（例如分类器）。另一种方法是“编码和预测”端到端范式，将不完整的数据编码为多任务学习的正确表示，包括插补和其他任务（例如分类和预测等）。尽管部分观察时间序列数据的最佳范式仍然是未来研究的开放领域，但后一种端到端方式被证明更有前途，特别是当嵌入缺失模式的信息有助于下游任务时[Miyaguchi等人，2021]。
可扩展性 虽然深度学习插补算法已显示出令人印象深刻的性能，但其计算成本通常超过基于统计和机器学习的同类算法。在数字数据蓬勃发展的时代，在通信和物联网设备进步的推动下，我们目睹了数据生成的指数级增长。这种激增，伴随着不完整数据集的普遍存在，对有效训练深度模型提出了重大挑战[Wu et al, 2023b]。具体来说，现有深度插补算法的高计算要求使得它们对于大规模数据集不太可行。因此，越来越需要可扩展的深度插补解决方案，利用并行和分布式计算技术来有效解决大规模缺失数据的挑战。
MTSI 的大型语言模型大型语言模型 (LLM) 促进了计算机视觉 (CV) 和自然语言处理 (NLP) 等领域的重大进步，最近在时间序列分析方面也取得了重大进展 [Jin 等人，2024]。法学硕士以其卓越的泛化能力而闻名，即使面对有限的数据集，也能表现出强大的预测性能。这一特性在 MTSI 背景下尤其有价值。法学硕士可以通过利用多模态知识巧妙地缩小这些数据差距，例如他们能够将额外的文本信息纳入分析中[Jin et al, 2023]，从而生成多模态嵌入。这种建模范式不仅通过提供更全面的数据理解和表示来丰富插补过程，而且还扩展了 MTSI 的视野。它可以包含不同的数据源，从而促进更详细和上下文感知的插补。探索 LLM 在 MTSI 中的集成代表了一个有前途的方向，有可能显着提高处理多元时间序列数据中缺失数据的功效和效率。