graphx翻译
overview
graphx是spark中的一个新的成员,用于图和图并行计算。它通过引入一个新的图抽象扩展了spark RDD:一个有向多元图,每个节点和边都有相应的属性。为了支持图计算,graphx开放了一系列基础操作符(比如subgraph,joinVertices和aggregateMessages),和Pregel API的优化版本一样。此外,graphx包含了一个不断增加的图算法和建立图的集合,用来精简图分析的任务。
Migrating from spark1.1
spark1.5.2中的Graphx包含一些用户接口API的变化:
1. 为了提高性能,我们引入了一个mapReduceTriplets的新版本,叫做aggregateMessages,它通过一个callback(EdgeContext)来获取从mapReduceTriplets得到的消息,而不是通过返回值。我们反对mapReduceTriplets,鼓励用户查阅transition guide。
2. 在spark1.0和1.1中
EdgeRDD的特性从EdgeRDD[ED]切换到EdgeRDD[ED,VD]来容许caching优化,我们因此发现了一个更优雅的解,将这个类型重塑为更自然的EdgeRDD[ED]类型。
Getting Started
graphx开始的第一步,你需要导入Spark和Graphx到你的程序中,如下:
import org.apache.spark._
import org.apache.spark.graphx._
// To make some of the examples work we will also need RDD
import org.apache.spark.rdd.RDD如果你不用Spark shell,你也需要一个SparkContext。
The Property Graph
属性图是一个有向多重图,每个节点和边都有用户定义的对象。一个有向多重图是一个有向的图,它有多个并行的边,这些边共享相同的源和目标节点。graphx这种支持并行边的能力简化了建模场景,像相同节点中有多重关系的情况。每个节点由唯一的一个64位长字符串标识。graphx没有对节点标识符施加任何顺序约束。相似的,边也有相应的源和目标节点标识符。
图的性质由节点(VD)和边(ED)类型参数化描述,它们是关联每个节点和边的目标类型。
graphx优化节点和边类型的表示,这些类型都是最初的数据类型(如int,double等),通过将它们存储在特定的序列中来降低内存。
一些情况下,需要在一幅图中有不同属性类型的节点,这可以通过继承来完成。比如,为将用户和商品描述为一个双边图,我们可以做以下操作:
class VertexProperty()
case class UserProperty(val name: String) extends VertexProperty
case class ProductProperty(val name: String, val price: Double) extends VertexProperty
// The graph might then have the type:
var graph: Graph[VertexProperty, String] = null如同RDDs,特征图是不可交互、分布式和错误容忍。对图中值和结构的改变通过新建一个图来完成,在这个图中添加你所希望的改变之处。注意到,原始图的本质部分(如未受影响的结构、属性等)会在新的图中再利用,从而减少继承函数结构的消耗。图通过一系列vertex partitioning heuristics来分割到不同executors。
逻辑上特征图对应一对RDDs,为每个节点和边描述特性。因此,图类包含成员来描述图中节点和边
class Graph[VD, ED] {
val vertices: VertexRDD[VD]
val edges: EdgeRDD[ED]
}类VertexRDD[VD]和EdgeRDD[ED]各自扩展、进一步在RDD[(VertexID,VD)]和RDD[Edge[ED]]优化。VertexRDD[VD]和EdgeRDD[ED]提供额外的函数。我们在vertex and edge RDDs中更详细讨论VertexRdd和EdgeRDD API,但现在它们可以看作RDD[(VertexID,VD)]和RDD[Edge[ED]]的简单RDDs形式。
Example Property Graph
假设我们构建一个包含各种各样协作者的特征图,节点特征可能包括用户名和职业,我们可以用字符串注释边从而描述协作者之间的关系。
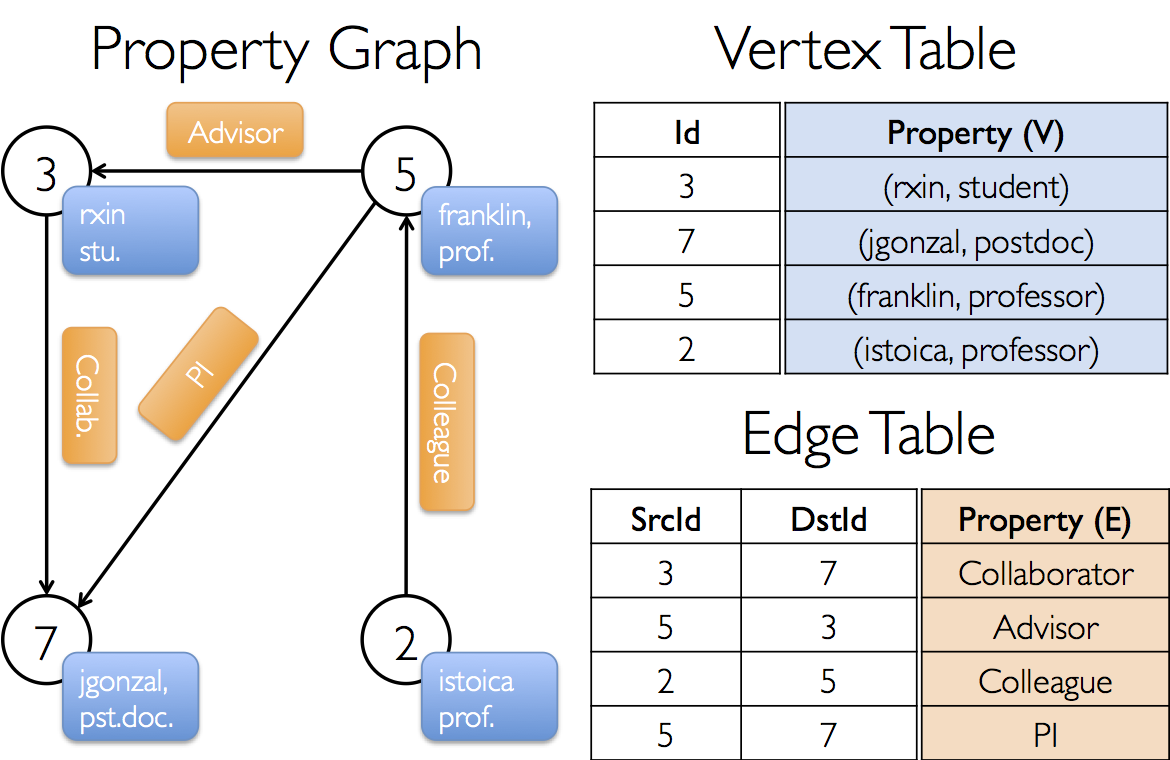
结果图将会有以下类型签名:
val userGraph: Graph[(String, String), String]
有很多方法可以从源文件、RDDs、以及合成发生器中构建特征图,这会在graph builders环节详细讨论。可能最通用的方法是使用Graph object,例如下面代码是从RDDs集合中构建图。
// Assume the SparkContext has already been constructed
val sc: SparkContext
// Create an RDD for the vertices
val users: RDD[(VertexId, (String, String))] =
sc.parallelize(Array((3L, ("rxin", "student")), (7L, ("jgonzal", "postdoc")),
(5L, ("franklin", "prof")), (2L, ("istoica", "prof"))))
// Create an RDD for edges
val relationships: RDD[Edge[String]] =
sc.parallelize(Array(Edge(3L, 7L, "collab"), Edge(5L, 3L, "advisor"),
Edge(2L, 5L, "colleague"), Edge(5L, 7L, "pi")))
// Define a default user in case there are relationship with missing user
val defaultUser = ("John Doe", "Missing")
// Build the initial Graph
val graph = Graph(users, relationships, defaultUser)在上面例子中,我们利用Edge类。Edge有一个scrID和一个dstID对应源和目标节点标识符,此外Edge类也有一个attr属性来存储边属性。
我们可以通过graph.vertices和graph.edges将图分解成节点和边两种视角。
val graph: Graph[(String, String), String] // Constructed from above
// Count all users which are postdocs
graph.vertices.filter { case (id, (name, pos)) => pos == "postdoc" }.count
// Count all the edges where src > dst
graph.edges.filter(e => e.srcId > e.dstId).count注意到graph.vertices返回一个VertexRDD[(String,String)],这个扩展了RDD[(VertexID,(String,String))],因此我们使用scala的case表达式来分解这个元组。另一方面,graph.edges返回一个EdgeRDD包含Edge[String]对象。我们也可以用case class类型的构造函数,如下所示
graph.edges.filter { case Edge(src, dst, prop) => src > dst }.count除了从节点和边的角度看特征图外,graphx也提供了三元组视角。这个三元组视角逻辑上联合节点和边特性,产出一个RDD[EdgeTriplet[VD,ED]],包括EdgeTriplet类的实例,这种联合可以标示为以下SQL表达:
SELECT src.id, dst.id, src.attr, e.attr, dst.attr
FROM edges AS e LEFT JOIN vertices AS src, vertices AS dst
ON e.srcId = src.Id AND e.dstId = dst.Id或者图形化表示为:

这个EdgeTriplet类通过增加srcAttr和dstAttr成员扩展Edge类,这两个成员包括源、目标特征。我们可以用图的三元组视角来产生描述用户间关系的字符串集合。
val graph: Graph[(String, String), String] // Constructed from above
// Use the triplets view to create an RDD of facts.
val facts: RDD[String] =
graph.triplets.map(triplet =>
triplet.srcAttr._1 + " is the " + triplet.attr + " of " + triplet.dstAttr._1)
facts.collect.foreach(println(_))Graph Operators
就像RDDs有基本操作符像map,filter,reduceByKey一样,特征图也有一系列基本操作符,这些操作符采用用户定义的函数,产生经过特征、结果变换后的新图。核心操作符优化Graph中定义的操作,便捷的操作符作为核心操作符的一种组成被定义在GraphOps中。然而,由于Scala在GraphOps隐式操作符。例如,我们可以计算一个节点的入度(在GraphOps中定义),如下
val graph: Graph[(String, String), String]
// Use the implicit GraphOps.inDegrees operator
val inDegrees: VertexRDD[Int] = graph.inDegrees区分图核心操作符与GraphOps可以支持不同的图表示,每个图表示必须提供核心操作符的执行和重用GpraphOps中有用的操作。
Summary List of Operators
以下是Graph和GraphOps中定义函数的总结,为了简化,被表示为Graph的成员。注意到一个函数标识已经被简化,一些更高级的函数功能已经被删除,所以查阅官方AIP文档
/** Summary of the functionality in the property graph */
class Graph[VD, ED] {
// Information about the Graph ===================================================================
val numEdges: Long
val numVertices: Long
val inDegrees: VertexRDD[Int]
val outDegrees: VertexRDD[Int]
val degrees: VertexRDD[Int]
// Views of the graph as collections =============================================================
val vertices: VertexRDD[VD]
val edges: EdgeRDD[ED]
val triplets: RDD[EdgeTriplet[VD, ED]]
// Functions for caching graphs ==================================================================
def persist(newLevel: StorageLevel = StorageLevel.MEMORY_ONLY): Graph[VD, ED]
def cache(): Graph[VD, ED]
def unpersistVertices(blocking: Boolean = true): Graph[VD, ED]
// Change the partitioning heuristic ============================================================
def partitionBy(partitionStrategy: PartitionStrategy): Graph[VD, ED]
// Transform vertex and edge attributes ==========================================================
def mapVertices[VD2](map: (VertexID, VD) => VD2): Graph[VD2, ED]
def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]
def mapEdges[ED2](map: (PartitionID, Iterator[Edge[ED]]) => Iterator[ED2]): Graph[VD, ED2]
def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]
def mapTriplets[ED2](map: (PartitionID, Iterator[EdgeTriplet[VD, ED]]) => Iterator[ED2])
: Graph[VD, ED2]
// Modify the graph structure ====================================================================
def reverse: Graph[VD, ED]
def