李超线段树

李超线段树

实现起来其实不算复杂

首先认识到我们插入的线段并不好来合并
那么我们选择不合并。

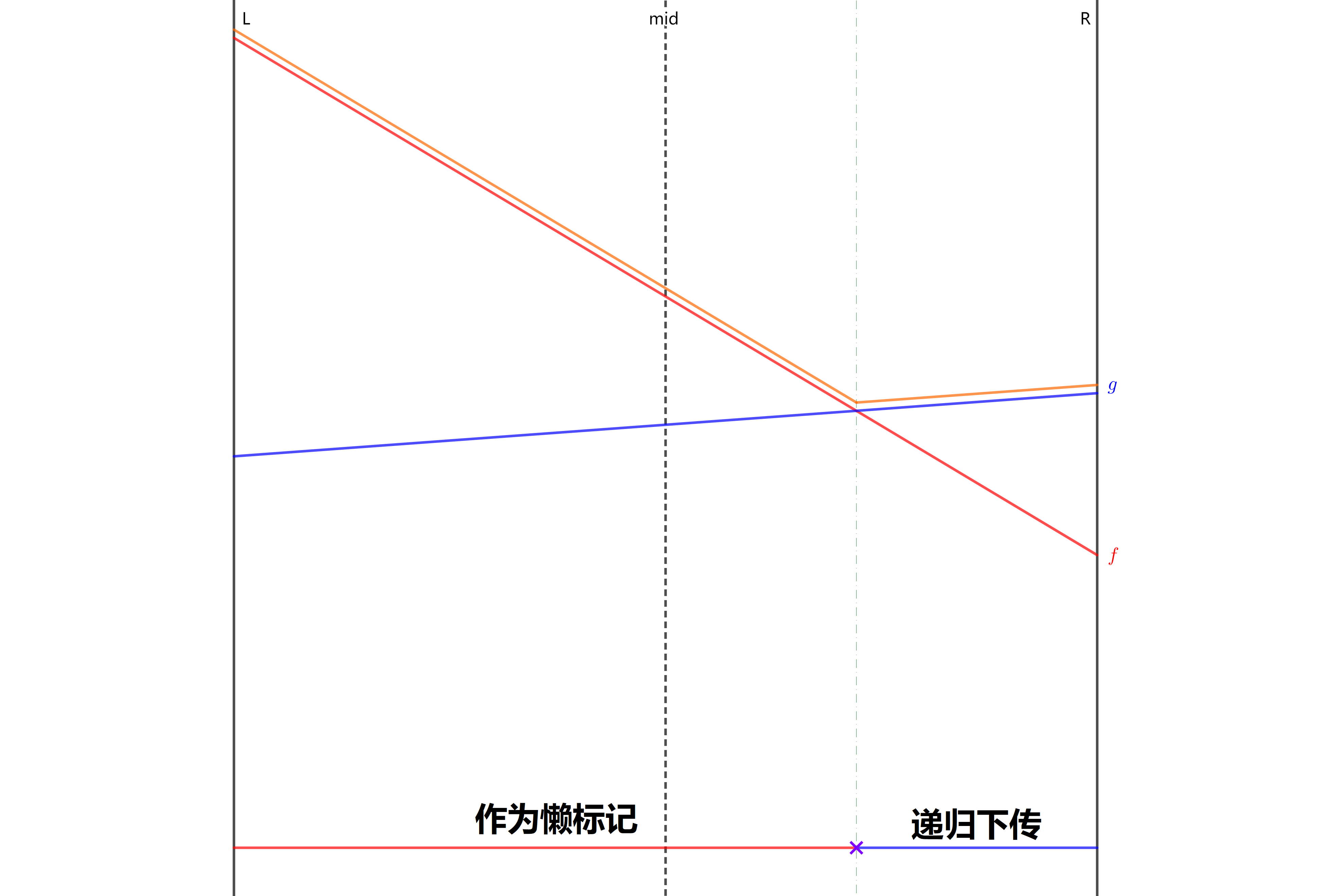
插入的操作是这样的：
首先对于新线段\(id\)如果中点值比原来的最优解大，我们\(swap\)一下
然后开始比较两边端点值：

• 如果左边\(id\)的值更大，说明左边还能继续更新。

• 右边同理

对着图片就能知道，这样是正确的，复杂度是\(O(log^2n)\)

贴一份代码：

#include<bits/stdc++.h>
#define int long long
#define dl long double
#define F(i,i0,n) for(int i=(i0);i<=(n);i++)
#define pii pair<int,int>
#define fr first
#define sc second
#define pb push_back
using namespace std;
inline int rd(){
    int f=0,x=0;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=1;ch=getchar();}
    while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-48;ch=getchar();}
    return f?-x:x;
}
const int N=4e6+500,mod=1e9+7;
const dl eps=1e-6;
struct Lng{dl k,b;}se[N];int cnt;
int bel[N];
void newlng(int x0,int y0,int x1,int y1){
	cnt++;
	if(x0==x1)se[cnt].k=0,se[cnt].b=max(y0,y1);
	else se[cnt].k=1.0*(y1-y0)/(x1-x0),se[cnt].b=y0-se[cnt].k*x0;
}
dl calc(int id,int x){return se[id].b+se[id].k*x;}
int cmp(dl a,dl b){
	if(a-b>eps)return 1;
	else if(b-a>eps)return -1;
	return 0;
}
#define ls (p<<1)
#define rs (p<<1|1)
#define mid ((l+r)>>1)
void chg(int p,int l,int r,int id){
	int &v=bel[p];
	int jud=cmp(calc(id,mid),calc(v,mid));
	if(jud==1)swap(v,id);
	int jud_l=cmp(calc(id,l),calc(v,l)),jud_r=cmp(calc(id,r),calc(v,r));
	if(jud_l==1)chg(ls,l,mid,id);
	if(jud_r==1)chg(rs,mid+1,r,id);
}
void upd(int p,int nl,int nr,int id,int l=0,int r=1e6+50){
	if(nl<=l&&r<=nr){chg(p,l,r,id);return ;}
	if(nl<=mid)upd(ls,nl,nr,id,l,mid);
	if(mid<nr)upd(rs,nl,nr,id,mid+1,r);
}
dl que(int p,int l,int r,int x){
	if(r<x||x<l)return LONG_LONG_MIN;
	if(l==r)return calc(bel[p],x);
	return max(calc(bel[p],x),max(que(ls,l,mid,x),que(rs,mid+1,r,x))) ;
}
int n,m;
signed main(){
	se[0].b=LONG_LONG_MIN;
	n=rd();
	m=rd();
	F(i,1,n){
		int x0=rd(),y0=rd(),x1=rd(),y1=rd();
		if(x0>x1)swap(x1,x0),swap(y0,y1); 
		if(x1<0)continue;
		newlng(x0,y0,x1,y1);
		upd(1,max(x0,0ll),x1,cnt);
	}
	F(i,1,m){
		int op=rd();
		if(!op){
			int x0=rd(),y0=rd(),x1=rd(),y1=rd();
			if(x0>x1)swap(x1,x0),swap(y0,y1); 
			if(x1<0)continue;
			newlng(x0,y0,x1,y1);
			upd(1,max(x0,0ll),x1,cnt);
		}
		else {
			int x=rd();
			dl k=que(1,0,1e6+50,x);
			printf("%.5Lf\n",k<=LONG_LONG_MIN?0.0:k);
		}
	}
	return 0;
}

如果是插入直线的话写起来会更简洁(贴的是基站建设的代码)：

#include<bits/stdc++.h>
#define int long long
#define F(i,i0,n) for(int i=(i0);i<=(n);i++)
#define pii pair<int,int>
#define dl double 
#define fr first
#define sc second
#define pb push_back
using namespace std;
inline int rd(){
    int f=0,x=0;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=1;ch=getchar();}
    while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-48;ch=getchar();}
    return f?-x:x;
}
const int N=5e5+5,mod=1e9+7;
struct Lng{
	dl k,b;
	dl f(int x){return k*x+b;}
}se[N];int cnt;
struct Seg{
	int son[2],bel;
}tr[N<<2];int tot;
int n,m;
struct Node{int x,r,v;}a[N];
dl dp[N];
#define mid ((l+r)>>1)
void upd(int &p,int l,int r,int id){
	if(p==0)p=++tot;
	if(se[tr[p].bel].f(mid)>se[id].f(mid))swap(tr[p].bel,id);
	if(l==r)return ;
	if(se[tr[p].bel].f(l)>se[id].f(l))upd(tr[p].son[0],l,mid,id);
	if(se[tr[p].bel].f(r)>se[id].f(r))upd(tr[p].son[1],mid+1,r,id);
}
dl que(int p,int l,int r,int x){
	if(!p)return 1e18;
	if(l==r)return se[tr[p].bel].f(x);
	dl ans=se[tr[p].bel].f(x);
	if(x<=mid)ans=min(ans,que(tr[p].son[0],l,mid,x));
	else ans=min(ans,que(tr[p].son[1],mid+1,r,x));
	return ans;
}
int rt;
void newlng(dl k,dl b){se[++cnt]={k,b};}
signed main(){
	n=rd(),m=rd();
	se[0].b=1e18;
	F(i,1,n)a[i].x=rd(),a[i].r=rd(),a[i].v=rd();
	dp[1]=a[1].v;
	newlng(1.0/(2*sqrt(a[1].r)),dp[1]-a[1].x/(2*sqrt(a[1].r)));
	upd(rt,a[1].x,a[n].x,cnt);
	F(i,2,n){
		dp[i]=que(1,a[1].x,a[n].x,a[i].x)+a[i].v;
		newlng(1.0/(2*sqrt(a[i].r)),dp[i]-a[i].x/(2*sqrt(a[i].r)));
		upd(rt,a[1].x,a[n].x,cnt);
	}
	dl ans=LONG_LONG_MAX;
	F(i,1,n)
		if(a[i].x+a[i].r>=m)
			ans=min(ans,dp[i]);
	printf("%.3lf\n",ans);
	return 0;
}