9.week2

这周准备初赛所以说做的题目很少,(主要是太菜了出的题目都没写完)

Challenges in school №41

由于你一定要反转逆序对数目,而且你只能一次换在一起的两个,所以说你在做冒泡排序.
这也是和题目里面答案小于\(n^2\)相匹配的.
那么就知道,最劣就是每次只换一个,最优就是换一个局面里面的所有.
我们考虑如何凑到\(k\)次,
其实很简单,就是在\(k>mn\)的时候换最劣情况,到了\(mn\)就上最优情况.
至于对正确性的保证什么的,直接看实现就懂了:

    while(1){
        int i=1;
        for(;i<n;++i){
            if(k==mn)break;
            if(a[i]==1&&a[i+1]==-1){
                swap(a[i],a[i+1]);
                k-=1;
                cout<<1<<' '<<i<<'\n';
                i+=1;
            }
        }
        top=0;
        for(;i<n;++i)if(a[i]==1&&a[i+1]==-1){
            st[++top]=i;
            swap(a[i],a[i+1]);
            i+=1;
        }
        if(top){
            cout<<top<<' ';
            k-=1;
            F(j,1,top)cout<<st[j]<<" ";
            cout<<'\n';
        }
        mn-=1;
        if(!k)break;
    }

我们确保了每一个最劣是基于对一个最优的拆解,保证每次的while只会走过一个\(mn\),这样就能保证了.

Visits S

\(n点n边\),鉴定为基环树题.
没有保证联通,所以说是基环树森林.
树上直接\(Topo\),因为这样就是最优的.
对于环上,直接就是断掉最小权值的边就行了.
挺基础的基环树dp(拜托你都没dp好吗).

Apple Catching G

来考虑一头奶牛能捡到苹果的条件(a牛,b苹果):

\[|a.x-b.x| \le a.t-b.t \]

就是 $ b.t-b.x \le a.t-a.x $ 和 $ b.x+b.t \le a.t+a.x $

这不是我们二维偏序的题吗.
我们考虑一种更好的处理这种二维偏序选点的贪心做法.

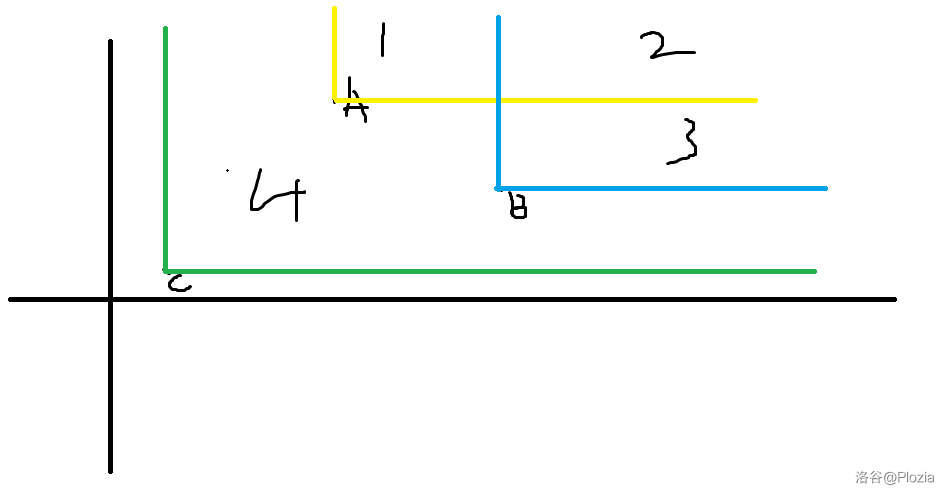
假设我们转换坐标系后变成了这样，有三头牛 A,B,C，一种正确的贪心方式如下：

先排序，横坐标为第一关键字降序，纵坐标为第二关键字降序，那么图中的点排序为 B,A,C。

然后依次选择苹果，对于每一个点而言，选择纵坐标最低的若干苹果，比如 B 点就会选 3 空间内的。

正确性就是因为 B 先选了 3 空间所以不会和 A 冲突，而 B 又在 C 前选所以保证 B 能选的尽量多，能匹配的就尽量多。

以上只是一种贪心方式，实际上还有几种方式也都是对的，比如排序调换关键字顺序后让 A 尽量选 1 空间之类的。

实现时用一个 multiset 维护即可，但是注意 multiset 删除值的时候会将所有与该值相等的键全删了，删迭代器就不会了。

很妙.

Phoenix and Computers

考虑连续段dp.
那么dp状态就是点亮了多少个(这个从代码中感觉一下,感觉这个题解写的有问题)和形成了多少连续段.
每个连续段预先分配两端的空格,以及你的操作只有扩展和新建,不能合并,合并会影响连续段意义的正确性
转移方程(去掉了难看的取模):

    dp[0][0]=1;//初始化
    F(i,1,n+1)F(j,0,i){
        dp[i][j]+=dp[i-1][j]*j*2;//选择接在之前的连续段上,那么就是每个连续段两个可能性的乘法原理
        if(i>=2&&j>=1)dp[i][j]+=dp[i-2][j-1]*j;//形成新的连续段,一个新的段是可以分配两个位置作为钦定已经点亮
    }

这里贴一个blog讲连续段dp的,连续段dp小记
有时间多学学?

Fafa and Ancient Alphabet

这个就很典了,直接分类dp就是的了.
其实是分类递推加贡献.
直接贴一个题解的分讨吧:

就这样了.