网络流学习笔记
注:本文不会提及网络流基础内容,建议学完EK、dinic等最大流算法后观看
网络流:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define inl inline
#define int ll
#define endl '\n'
#define gc cin.get
#define pc cout.put
const int N=2e2+5;
const int M=1e4+5;
const int inf=0x3f3f3f3f3f3f3f3f;
const int mod=1e9+7;
inl int read(){
int x=0,f=1;char c=gc();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=gc();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=gc();}
return x*f;
}
inl void write(int x){
if(x<0){pc('-');x=-x;}
if(x>9)write(x/10);
pc(x%10+'0');
}
inl void writei(int x){write(x);pc(' ');}
inl void writel(int x){write(x);pc('\n');}
int n,m,s,t,dis[N],cur[N],maxflow;
int head[N],nxt[M],to[M],w[M],cnt(1);
inl void add(int u,int v,int wi){
nxt[++cnt]=head[u];to[cnt]=v;w[cnt]=wi;head[u]=cnt;
nxt[++cnt]=head[v];to[cnt]=u;w[cnt]=0;head[v]=cnt;
}
queue<int>q;
inl bool bfs(){
memset(dis,0,sizeof dis);
memcpy(cur,head,sizeof cur);
q.push(s);dis[s]=1;
while(!q.empty()){
int x=q.front();q.pop();
for(int i=head[x];i;i=nxt[i]){
int y=to[i],wi=w[i];
if(wi&&!dis[y]){
dis[y]=dis[x]+1;
q.push(y);
}
}
}
return dis[t];
}
inl int dfs(int x,int flow){
if(x==t)return maxflow+=flow,flow;
int used=0,rlow;
for(int &i=cur[x];i;i=nxt[i]){
int y=to[i],wi=w[i];
if(wi&&dis[y]==dis[x]+1){
if(rlow=dfs(y,min(wi,flow-used))){
w[i]-=rlow;w[i^1]+=rlow;
used+=rlow;
if(used==flow)break;
}
}
}
return used;
}
inl void dinic(){while(bfs())dfs(s,inf);}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
n=read();m=read();s=read();t=read();
for(int i=1;i<=m;i++){
int u=read(),v=read(),wi=read();
add(u,v,wi);
}
dinic();
cout<<maxflow<<endl;
return 0;
}
复杂度上界 \(O(n^2m)\) 实际中远远达不到
国王louis曾说过:
可以认为网络流dinic可以处理\(\le 10^5\) 的图
一些注意事项(都是血的教训:
- 链前 cnt=1
- 如果你在bfs中
return dis[t]^inf;注意inf值和你是否#define int ll - bfs中pop出去的值
vis[x]=0 - 写网络流注意卡空间:尽量让点和边的数组卡到数据量上界 不要开的特别大
memset分分钟教你做人 - dfs中注意当前弧优化
- 如果你dfs中的for循环有如下写法:
恭喜你 假了inl int dfs(int x,int flow){ ··· for(int &i=cur[x];i&&used<flow;i=nxt[i]) ··· return used; }i&&used<flow没有起到任何作用 他会用used初值0一直和flow比较
建议如下写法:
这东西不会对正确性有任何影响 但会严重影响运行效率for(int &i=cur[x];i;i=nxt[i]){ int y=to[i],wi=w[i]; if(wi&&dis[y]==dis[x]+1){ if(rlow=dfs(y,min(wi,flow-used))){ w[i]-=rlow;w[i^1]+=rlow; used+=rlow; if(used==flow)break; } } }
luogu 模板 \(57ms->947ms\)
费用流:
翻了下费用流的题解区 发现全是EK 没有一个重口味zkw费用流
粘个自己板子:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define inl inline
#define endl '\n'
#define gc cin.get
#define pc cout.put
const int N=5e3+5;
const int M=5e4+5;
const int inf=0x3f3f3f3f;
const int mod=1e9+7;
inl int read(){
int x=0,f=1;char c=gc();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=gc();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=gc();}
return x*f;
}
inl void write(int x){
if(x<0){pc('-');x=-x;}
if(x>9)write(x/10);
pc(x%10+'0');
}
inl void writei(int x){write(x);pc(' ');}
inl void writel(int x){write(x);pc('\n');}
int n,m,s,t,dis[N],vis[N],cur[N],maxflow,mincost;
int head[N],nxt[M<<1],to[M<<1],w[M<<1],c[M<<1],cnt=1;
inl void add(int u,int v,int wi,int ci){
nxt[++cnt]=head[u];to[cnt]=v;w[cnt]=wi;c[cnt]=ci;head[u]=cnt;
nxt[++cnt]=head[v];to[cnt]=u;w[cnt]=0;c[cnt]=-ci;head[v]=cnt;
}
inl bool spfa(){
memset(dis,0x3f,sizeof dis);
memcpy(cur,head,sizeof cur);
queue<int>q;
dis[s]=0;vis[s]=1;q.push(s);
while(!q.empty()){
int x=q.front();q.pop();vis[x]=0;
for(int i=head[x];i;i=nxt[i]){
int y=to[i],wi=w[i],ci=c[i];
if(wi&&dis[y]>dis[x]+ci){
dis[y]=dis[x]+ci;
if(!vis[y]){q.push(y);vis[y]=1;}
}
}
}
return dis[t]^inf;
}
inl int dfs(int x,int flow){
if(x==t)return maxflow+=flow,flow;
vis[x]=1;
int rlow,used=0;
for(int &i=cur[x];i;i=nxt[i]){
int y=to[i],wi=w[i],ci=c[i];
if(!vis[y]&&wi&&dis[y]==dis[x]+ci){
if(rlow=dfs(y,min(wi,flow-used))){
w[i]-=rlow;
w[i^1]+=rlow;
mincost+=rlow*ci;
used+=rlow;
if(used==flow)break;
}
}
}
vis[x]=0;
return used;
}
inl void dinic(){
while(spfa())dfs(s,inf);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
n=read();m=read();s=read();t=read();
for(int i=1;i<=m;i++){
int u=read(),v=read(),w=read(),c=read();
add(u,v,w,c);
}
dinic();
cout<<maxflow<<' '<<mincost<<endl;
return 0;
}
可以发现 与刚才的网络流代码神似 极其好背
不同之处:
- bfs -> spfa
- dfs 中注意统计vis 可以理解为分层图
因为原来网络流 dis 其实就是层数 而费用流 dis 就是费用 无法确定层数
否则会无限递归喜提MLE
网络流常见建模技巧:
1.超级源点和超级汇点
非常常见且实用的技巧
在图中存在大量源/汇点时 可以考虑建超级源/汇点 向他们连边 可以减轻建图难度
2.拆点/拆边
1)神秘限制
如果对于图中的一条边 要求只通过一次 显然让流量为 \(1\) 即可
那要求一个点只经过一次呢?
可以拆点解决:把一个点拆成入点和出点 连向他的边都接到入点上 出边都从出点出去
再让入点向出点连流量为1的边 这样就解决了
如果要求一个边可以走多次 贡献只能算一次呢?
可以把这条边拆成 流量为 \(1\) 费用为 \(v\) 的边 和 流量为 \(inf\) 贡献为 \(0\) 的边即可
2)时间
如果题目中出现不同时间费用不同的情况,可以考虑把每个点按时间拆点。
[SCOI2007] 修车
可以发现,朴素连边就是把车和技师分别开点,然后二分图匹配。
但这样显然无法搞定后面的人等待时间要加上前面时间总和
可以发现 假设技师 \(x\) 总共修了 \(k\) 辆车 那么时间总和:
那么我们可以让一辆车一次累加完自己的贡献 把每个技师拆成 \(n\) 个点 \((x,k)\) 代表第 \(x\) 个技师 修倒数第 \(k\) 辆车的时间贡献
从第 \(j\) 辆车连边 \(c_{x,j}\times k\) 到 \((x,k)\) 即可
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define inl inline
#define endl '\n'
#define int ll
#define gc cin.get
#define pc cout.put
const int N=1e5+5;
const int M=1e7+5;
const int inf=0x3f3f3f3f3f3f3f3f;
const int mod=1e9+7;
inl int read(){
int x=0,f=1;char c=gc();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=gc();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=gc();}
return x*f;
}
inl void write(int x){
if(x<0){pc('-');x=-x;}
if(x>9)write(x/10);
pc(x%10+'0');
}
inl void writei(int x){write(x);pc(' ');}
inl void writel(int x){write(x);pc('\n');}
int n,m,ans,vis[N],dis[N],cur[N],s,t,mincost,p[N],sum,tim[45][105],top[N],viss[M];
int head[N],nxt[M],to[M],w[M],c[M],cnt=1;
inl void add(int u,int v,int wi,int ci){
nxt[++cnt]=head[u];to[cnt]=v;w[cnt]=wi;c[cnt]=ci;head[u]=cnt;
nxt[++cnt]=head[v];to[cnt]=u;w[cnt]=0;c[cnt]=-ci;head[v]=cnt;
}
queue<int>q;
vector<int>v;
inl bool spfa(){
memset(dis,0x3f,sizeof dis);
memcpy(cur,head,sizeof cur);
dis[s]=0;q.push(s);
while(!q.empty()){
int x=q.front();q.pop();vis[x]=0;
for(int i=head[x];i;i=nxt[i]){
int y=to[i],wi=w[i],ci=c[i];
if(wi&&dis[y]>dis[x]+ci){
dis[y]=dis[x]+ci;
if(!vis[y]){vis[y]=1;q.push(y);}
}
}
}
return dis[t]^inf;
}
inl int dfs(int x,int flow){
if(x==t)return flow;
vis[x]=1;int used=0,rlow;
for(int &i=cur[x];i;i=nxt[i]){
int y=to[i],wi=w[i],ci=c[i];
if(!vis[y]&&wi&&dis[y]==dis[x]+ci){
if(rlow=dfs(y,min(wi,flow-used))){
w[i]-=rlow;w[i^1]+=rlow;
mincost+=rlow*ci;
used+=rlow;
if(used==flow)break;
}
}
}
vis[x]=0;
return used;
}
inl void dinic(){
while(spfa()){
dfs(s,inf);
for(int i=head[t];i;i=nxt[i]){
if(viss[i])continue;
int y=to[i],wi=w[i];
if(!wi)continue;
int k=(y-n-1)/sum+1;
viss[i]=1;
top[k]++;
if(top[k]+1>sum)continue;
for(int x=1;x<=n;x++)
add(x,n+(k-1)*sum+top[k]+1,1,tim[x][k]*(top[k]+1));
add(n+(k-1)*sum+top[k]+1,t,1,0);
}
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
n=read();m=read();
for(int i=1;i<=n;i++)
p[i]=read(),sum+=p[i];
s=n+sum*m+1;t=n+sum*m+2;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
tim[i][j]=read();
add(i,n+(j-1)*sum+1,1,tim[i][j]);
}
}
for(int i=1;i<=n;i++)add(s,i,p[i],0);
for(int i=1;i<=m;i++)add(n+(i-1)*sum+1,t,1,0);
dinic();
cout<<mincost<<endl;
return 0;
}
3.最小割
最小割
假如给你一个图,边有边权,然后让你在割掉边权和最小情况下把两个点分开,那么这个割掉的最小边权和就是这个图的最小割。
一个耳熟能详的结论:最大流=最小割
太菜只会感性证明:
首先跑最大流增广时流量一定会被最小割限制住,即最大流 \(\le\) 最小割
而如果流量小于最小割 图中就一定存在一条增广路可以让最大流增加,即最大流 \(\ge\) 最小割
综上,最大流=最小割。
P1344 [USACO4.4] 追查坏牛奶 Pollutant Control
首先这题第一问很简单 最小割模板
那么怎样让割边数量最小 这里只需要将边权赋为 \(w_i\times(m+1)+1\) 即可
这样+1数量不超过 \(m\) 不会影响原来最小流的答案 而且求出最大流 \(\bmod m+1\) 即为最小割边数
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define inl inline
#define endl '\n'
#define int ll
#define gc cin.get
#define pc cout.put
const int N=1e2+5;
const int M=1e4+5;
const int inf=0x3f3f3f3f3f3f3f3f;
const int mod=1e9+7;
inl int read(){
int x=0,f=1;char c=gc();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=gc();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=gc();}
return x*f;
}
inl void write(int x){
if(x<0){pc('-');x=-x;}
if(x>9)write(x/10);
pc(x%10+'0');
}
inl void writei(int x){write(x);pc(' ');}
inl void writel(int x){write(x);pc('\n');}
int n,m,rt,dis[N],cur[N],s,t,maxflow;
int head[N],to[M],nxt[M],w[M],cnt=1;
inl void add(int u,int v,int wi){
nxt[++cnt]=head[u];to[cnt]=v;w[cnt]=wi;head[u]=cnt;
nxt[++cnt]=head[v];to[cnt]=u;w[cnt]=0;head[v]=cnt;
}
queue<int>q;
struct edge{
int u,v,wi;
}e[M];
inl bool bfs(){
memset(dis,0,sizeof dis);
memcpy(cur,head,sizeof cur);
dis[s]=1;q.push(s);
while(!q.empty()){
int x=q.front();q.pop();
for(int i=head[x];i;i=nxt[i]){
int y=to[i],wi=w[i];
if(wi&&!dis[y]){
dis[y]=dis[x]+1;
q.push(y);
}
}
}
return dis[t];
}
inl int dfs(int x,int flow){
if(x==t)return maxflow+=flow,flow;
int used=0,rlow;
for(int &i=cur[x];i;i=nxt[i]){
int y=to[i],wi=w[i];
if(wi&&dis[y]==dis[x]+1){
if(rlow=dfs(y,min(wi,flow-used))){
w[i]-=rlow;w[i^1]+=rlow;
used+=rlow;
if(used==flow)continue;
}
}
}
return used;
}
inl void dinic(){while(bfs())dfs(s,inf);}
signed main(){
n=read();m=read();
s=1,t=n;
for(int i=1;i<=m;i++){
int u=read(),v=read(),wi=read();
e[i]={u,v,wi};
add(u,v,wi);
}
dinic();cout<<maxflow<<' ';
memset(head,0,sizeof head);
memset(nxt,0,sizeof nxt);
cnt=1,maxflow=0;
for(int i=1;i<=m;i++){
int u=e[i].u,v=e[i].v,wi=e[i].wi*(m+1)+1;
add(u,v,wi);
}
dinic();cout<<maxflow%(m+1)<<' ';
return 0;
}
对偶图
顺带说一下吧。
最大流=最小割=对偶图最短路
[ICPC-Beijing 2006] 狼抓兔子
我们把边围出的区域当成一个点,每条边连接他分开的两个区域。
我们从左下角向右上角连边 那么就是一个对偶图 可以发现最短路就是原图分开s和t的最小割 剩下就是最短路了
双倍经验
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define inl inline
#define endl '\n'
#define int ll
#define gc cin.get
#define pc cout.put
#define id(i,j,k) idx[i][j][k]?idx[i][j][k]:idx[i][j][k]=++num
const int N=2e6+5;
const int M=1e7+5;
const int inf=0x3f3f3f3f3f3f3f3f;
const int mod=1e9+7;
inl int read(){
int x=0,f=1;char c=gc();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=gc();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=gc();}
return x*f;
}
inl void write(int x){
if(x<0){pc('-');x=-x;}
if(x>9)write(x/10);
pc(x%10+'0');
}
inl void writei(int x){write(x);pc(' ');}
inl void writel(int x){write(x);pc('\n');}
int n,m,idx[1005][1005][2],num,s,t,dis[N],vis[N];
int head[N],nxt[M],to[M],w[M],cnt;
inl void add(int u,int v,int c){
nxt[++cnt]=head[u];
to[cnt]=v;w[cnt]=c;
head[u]=cnt;
}
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>q;
inl void dij(){
memset(dis,0x3f,sizeof dis);
dis[s]=0;q.push({0,s});
while(!q.empty()){
int x=q.top().second;q.pop();
if(vis[x])continue;vis[x]=1;
for(int i=head[x];i;i=nxt[i]){
int y=to[i],c=w[i];
if(dis[y]>dis[x]+c){
dis[y]=dis[x]+c;
q.push({dis[y],y});
}
}
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
n=read();m=read();
s=++num,t=++num;
for(int i=1;i<=m-1;i++)add(id(1,i,1),t,read());
for(int i=2;i<=n-1;i++)
for(int j=1;j<=m-1;j++){
int v=read();
add(id(i,j,1),id(i-1,j,0),v);
add(id(i-1,j,0),id(i,j,1),v);
}
for(int i=1;i<=m-1;i++)add(s,id(n-1,i,0),read());
for(int i=1;i<=n-1;i++){
add(s,id(i,1,0),read());
for(int j=2;j<=m-1;j++){
int v=read();
add(id(i,j-1,1),id(i,j,0),v);
add(id(i,j,0),id(i,j-1,1),v);
}
add(id(i,m-1,1),t,read());
}
for(int i=1;i<=n-1;i++)
for(int j=1;j<=m-1;j++){
int v=read();
add(id(i,j,0),id(i,j,1),v);
add(id(i,j,1),id(i,j,0),v);
}
dij();
cout<<dis[t]<<endl;
return 0;
}
最大权闭合子图
一个很有意思的模型。
P3410 拍照
题目简述:
给定 \(n\) 个点,如果同时选一些点可以得到 \(w_i\) 利润,但选一个点需要 \(c_j\) 花费。
先给出一些概念:
- 闭合子图:一幅图中每个点,以及每个点的出边的点都在这幅图中,也就是这幅图中的所有点的出边都是指向子图内部的。
- 最大权闭合子图:在所有的闭合子图中,它所包含的子图的点的点权之和是最大的。
可以发现 我们如果连边 就是在求图中的最大权闭合子图
考虑如下建图方式:
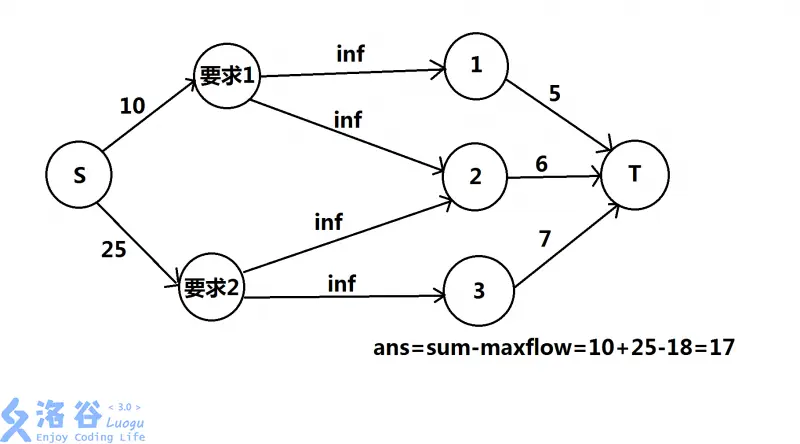
(借用题解区大佬一张图
对于所有利润 连 \(s->x\) 边权为利润
对于所有花费 连 \(x->t\) 边权为花费
中间点连边权为 \(inf\) 的边
这样建图有什么用呢
对于这张图的最小割 首先必然不会割掉中间流量为 \(inf\) 的边(求的是最小割啊喂)
其次 如果割掉了 \(s->x\) 的边 那么代表放弃当前组合
然后 如果割掉了 \(x->t\) 的边 那么代表选择当前的点
这东西看起来莫名其妙 不过接下来应该就明白了
首先 如果要选当前组合 那么就要求他出边指向的点全选
如果 这些点存在一个点 连到 \(t\) 的边没被割 此时存在一条 \(s\) 到 \(t\) 的增广路
根据刚才的意义 此时相当于既选该方案 又不选这个方案中的点 显然不行
此时会再次增广 即割掉 \(s->x\) 或 \(y->t\) 阻止错误发生
也就是说 只有图中不存在增广路,或者说 \(s\) \(t\) 不联通时才满足要求
这时 图中的最小割=不选的组合的利润+选的点的花费
显然 总利润-最小割 就是最后的答案了
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define inl inline
#define endl '\n'
#define int ll
#define gc cin.get
#define pc cout.put
const int N=2e2+5;
const int M=1e5+5;
const int inf=0x3f3f3f3f3f3f3f3f;
const int mod=1e9+7;
inl int read(){
int x=0,f=1;char c=gc();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=gc();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=gc();}
return x*f;
}
inl void write(int x){
if(x<0){pc('-');x=-x;}
if(x>9)write(x/10);
pc(x%10+'0');
}
inl void writei(int x){write(x);pc(' ');}
inl void writel(int x){write(x);pc('\n');}
int n,m,s,t,dis[N],vis[N],cur[N],maxflow;
int head[N],nxt[M],to[M],w[M],cnt=1;
inl void add(int u,int v,int c){
nxt[++cnt]=head[u];to[cnt]=v;w[cnt]=c;head[u]=cnt;
nxt[++cnt]=head[v];to[cnt]=u;w[cnt]=0;head[v]=cnt;
}
queue<int>q;
inl bool bfs(){
memset(dis,0,sizeof dis);
memcpy(cur,head,sizeof head);
dis[s]=1;q.push(s);
while(!q.empty()){
int x=q.front();q.pop();
for(int i=head[x];i;i=nxt[i]){
int y=to[i],wi=w[i];
if(wi&&!dis[y]){
dis[y]=dis[x]+1;
q.push(y);
}
}
}
return dis[t];
}
inl int dfs(int x,int flow){
if(x==t)return maxflow+=flow,flow;
int used=0,rlow;
for(int &i=cur[x];i;i=nxt[i]){
int y=to[i],wi=w[i];
if(wi&&dis[y]==dis[x]+1){
if(rlow=dfs(y,min(wi,flow-used))){
w[i]-=rlow;w[i^1]+=rlow;
used+=rlow;
if(used==flow)continue;
}
}
}
return used;
}
inl void dinic(){while(bfs())dfs(s,inf);}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
m=read();n=read();
s=n+m+1,t=n+m+2;int ans=0;
for(int i=1;i<=m;i++){
int v=read();ans+=v;
add(s,i,v);
while(int x=read())
add(i,m+x,inf);
}
for(int i=1;i<=n;i++)
add(m+i,t,read());
dinic();
cout<<ans-maxflow<<endl;
return 0;
}
4.上下界网络流
给定无源汇流量网络 \(G\) ,询问是否存在一种标定每条边流量的方式,使得每条边流量满足上下界同时每一个点流量平衡。
解法:
1.建立超源超汇 \(s\) , \(t\)
2.下界流量必然跑完,那么把贡献先累加
假如一条边的流量要求在 \([l,r]\) 之间,那么原图连容量为 \(r-l\) 的边 其余不变
3.对于每个点求出流入和流出的下界流量和 令 \(d_i\) 为 该点流入的下界流量-流出的下界流量
- 如果 \(d_i=0\) 那么正好流完
- 如果 \(d_i>0\) 下界流入比流出多 那么我们砍去下界之后 需要补流 从 \(s\) 连容量为 \(d_i\) ,费用为 \(0\) 的边
- 如果 \(d_i<0\) 下界流入比流出少 那么我们砍去下界之后 需要补流 向 \(t\) 连容量为 \(-d_i\) ,费用为 \(0\) 的边
如果原图是有源汇的 从汇点连回源点 就是无源汇了


 浙公网安备 33010602011771号
浙公网安备 33010602011771号