CF600

CF600A

按题意模拟即可。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
#define inl inline
#define mid (l+r>>1)
const int N=1e5+5;
const int M=1e5+5;
const int mod=1e5+3;
inl int read(){
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return x*f;
}
inl void write(int x){
    if(x<0){x=-x;putchar('-');}
    if(x>9)write(x/10);
    putchar(x%10+'0');
}
inl void writel(int x){write(x);putchar('\n');}
int n,flag=1;
string s,t,ans1,ans2;
signed main(){
    cin>>s;
    for(auto i:s){
        if(i==','||i==';'){
            if(flag&&!t.empty()&&!(t.size()>1&&t[0]=='0'))ans1+=t+',';
            else ans2+=t+',';
            t.clear();flag=1;
            continue;
        }
        t+=i;
        if(!isdigit(i))flag=0;
    }
    if(flag&&!t.empty()&&!(t.size()>1&&t[0]=='0'))ans1+=t+',';
    else ans2+=t+',';
    if(!ans1.empty())cout<<'"'+ans1.substr(0,ans1.size()-1)+'"'<<endl;
    else cout<<'-'<<endl;
    if(!ans2.empty())cout<<'"'+ans2.substr(0,ans2.size()-1)+'"'<<endl;
    else cout<<'-'<<endl;
    return 0;
}

CF600B

权值树状数组，离散化后插入a，查询b即可

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
#define inl inline
const int N=4e5+5;
const int M=1e5+5;
const int mod=1e5+3;
inl int read(){
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return x*f;
}
inl void write(int x){
    if(x<0){x=-x;putchar('-');}
    if(x>9)write(x/10);
    putchar(x%10+'0');
}
inl void writel(int x){write(x);putchar('\n');}
int n,m,a[N],b[N],lsh[N],c[N],t;
inl void add(int x){
    for(;x<=t;x+=x&-x)c[x]++;
}
inl int query(int x){
    int ans=0;
    for(;x;x-=x&-x)ans+=c[x];
    return ans;
}
signed main(){
    n=read();m=read();
    for(int i=1;i<=n;i++)a[i]=lsh[i]=read();
    for(int i=1;i<=m;i++)b[i]=lsh[i+n]=read();
    sort(lsh+1,lsh+n+m+1);
    t=unique(lsh+1,lsh+n+m+1)-lsh-1;
    for(int i=1;i<=n;i++)a[i]=lower_bound(lsh+1,lsh+t+1,a[i])-lsh;
    for(int i=1;i<=m;i++)b[i]=lower_bound(lsh+1,lsh+t+1,b[i])-lsh;
    for(int i=1;i<=n;i++)add(a[i]);
    for(int i=1;i<=m;i++)writel(query(b[i]));
    return 0;
}

然而只需要把a排序 b再二分找第一个小于他的a

CF600C

题面有坑：要求字典序最小（做CF题好习惯：先去讨论区看翻译锅没锅）

有影响的只有出现次数为奇数的字母 那么把字典序大的换成字典序最小的即可

如果剩下一个特判一下即可

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
#define inl inline
#define mid (l+r>>1)
const int N=1e5+5;
const int M=1e5+5;
const int mod=1e5+3;
inl int read(){
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return x*f;
}
inl void write(int x){
    if(x<0){x=-x;putchar('-');}
    if(x>9)write(x/10);
    putchar(x%10+'0');
}
inl void writel(int x){write(x);putchar('\n');}
int n,cnt[N],flag;
string s;
vector<int>v;
signed main(){
    cin>>s;
    for(auto i:s)cnt[i-'a'+1]++;
    for(int i=1;i<=26;i++){
        if(!(cnt[i]&1))continue;
        v.push_back(i);
    }
    for(int l=0,r=v.size()-1;l<r;l++,r--)cnt[v[r]]--,cnt[v[l]]++;
    flag=0;v.clear();
    for(int i=1;i<=26;i++){
        if(cnt[i]&1)flag=i,cnt[i]--;
        while(cnt[i])v.push_back(i),cnt[i]-=2;
    }
    for(auto i:v)putchar(i+'a'-1);
    if(flag)putchar(flag+'a'-1);
    reverse(v.begin(),v.end());
    for(auto i:v)putchar(i+'a'-1);
    return 0;
}

CF600D

高中数学题。

特判不相交/包含的两种特殊情况 剩下的都是两个扇形拼起来(额叫它扇形好像不太对

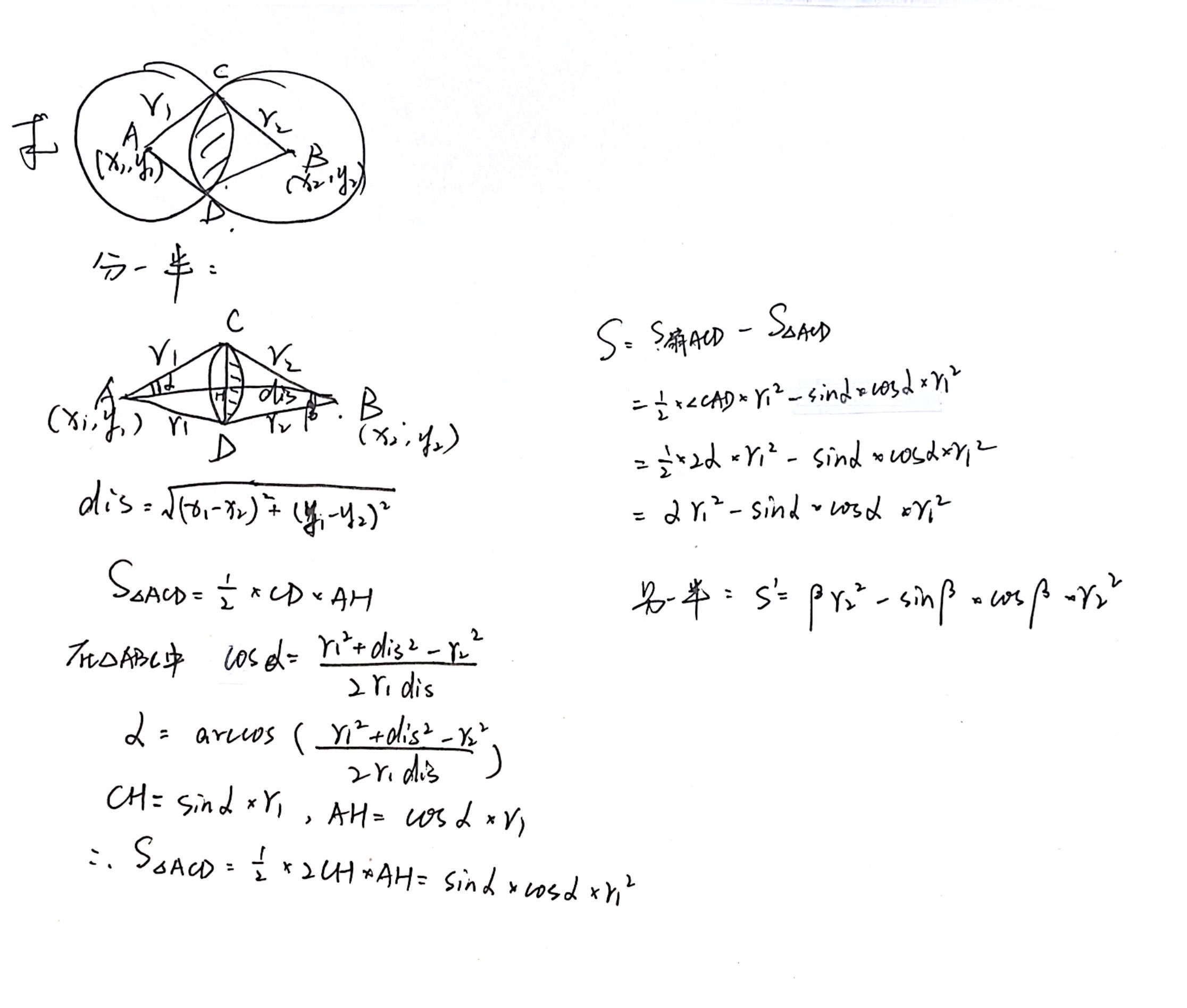
字迹有点乱()

注意要一步推出结果不要一点一点求（也不要图简单用海伦公式）

否则精度会炸 可以开个 long double

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
#define inl inline
const int N=1e5+5;
const int M=1e5+5;
const int mod=1e5+3;
inl int read(){
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return x*f;
}
inl void write(int x){
    if(x<0){x=-x;putchar('-');}
    if(x>9)write(x/10);
    putchar(x%10+'0');
}
inl void writel(int x){write(x);putchar('\n');}
long double n,x,y,r1,xx,yy,r2,ans,deg,len,h,ans2,ans1,dis;
signed main(){
    cin>>x>>y>>r1>>xx>>yy>>r2;
    dis=sqrt((x-xx)*(x-xx)+(y-yy)*(y-yy));
    if(dis>=r1+r2){printf("%.20f\n",0);return 0;}
    if(dis<=fabs(r1-r2)){printf("%.20Lf\n",min(r1,r2)*min(r1,r2)*acos(-1));return 0;}
    deg=acos((r1*r1+dis*dis-r2*r2)/(2*r1*dis));
    ans=deg*r1*r1-sin(deg)*r1*cos(deg)*r1;
    deg=acos((r2*r2+dis*dis-r1*r1)/(2*r2*dis));
    ans+=deg*r2*r2-sin(deg)*r2*cos(deg)*r2;
    printf("%.20Lf\n",ans);
    return 0;
}

CF600E

发现只有查询没有修改&只查询子树内信息 dsu on tree模版题

每次递归到子树求答案 返回前清空 但重儿子不要清

这样回到当前节点只要加上轻儿子和自己的贡献即可

复杂度 \(O(n\log n)\) 虽然我不会证

注意清空不要memset 否则复杂度就回到 \(O(n^2)\) 了

可以用dfs序循环直接清 个人觉得比递归写法简单 常数还小

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
#define inl inline
#define int ll
const int N=2e5+5;
const int M=1e5+5;
const int mod=1e5+3;
inl int read(){
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return x*f;
}
inl void write(int x){
    if(x<0){x=-x;putchar('-');}
    if(x>9)write(x/10);
    putchar(x%10+'0');
}
inl void writei(int x){write(x);putchar(' ');}
inl void writel(int x){write(x);putchar('\n');}
int n,c[N],u,v,res[N],rev[N],sum[N],ma,ans;
int head[N],nxt[N],to[N],cnt;
int siz[N],son[N],pos[N],dfn;
inl void add(int u,int v){
    nxt[++cnt]=head[u];
    to[cnt]=v;
    head[u]=cnt;
}
inl void dfs1(int x,int fa){
    siz[x]=1;
    for(int i=head[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa)continue;
        dfs1(y,x);
        siz[x]+=siz[y];
        if(siz[y]>siz[son[x]])son[x]=y;
    }
}
inl void update(int x){
    for(int i=pos[x];i<=pos[x]+siz[x]-1;i++){
        sum[c[rev[i]]]++;
        if(sum[c[rev[i]]]==ma)ans+=c[rev[i]];
        if(sum[c[rev[i]]]>ma)ma=sum[c[rev[i]]],ans=c[rev[i]];
    }
}
inl void del(int x){
    ma=ans=0;
    for(int i=pos[x];i<=pos[x]+siz[x]-1;i++)sum[c[rev[i]]]--;
}
inl void dfs2(int x,int fa,int flag){
    pos[x]=++dfn;rev[dfn]=x;
    for(int i=head[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa||y==son[x])continue;
        dfs2(y,x,0);
    }
    if(son[x])dfs2(son[x],x,1);
    for(int i=head[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa||y==son[x])continue;
        update(y);
    }
    sum[c[x]]++;
    if(sum[c[x]]==ma)ans+=c[x];
    if(sum[c[x]]>ma)ma=sum[c[x]],ans=c[x];
    res[x]=ans;
    if(!flag)del(x);
}
signed main(){
    n=read();
    for(int i=1;i<=n;i++)c[i]=read();
    for(int i=1;i<=n-1;i++){
        u=read();v=read();
        add(u,v);add(v,u);
    }dfs1(1,0);dfs2(1,0,1);
    for(int i=1;i<=n;i++)writei(res[i]);
    return 0;
}

还有线段树合并做法：每个点开个主席树 初始只有当前节点信息 然后儿子统计完之后并上来

复杂度 \(O(n\log n)\) 我还是不会证

注意合并时如果每次都并到原来节点 会对之前节点树的结构产生破坏 所以每次并完先统计答案

（也可以合并时新开节点 但空间可能会炸）

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
#define inl inline
#define mid (l+r>>1)
#define int ll
const int N=2e5+5;
const int M=1e5+5;
const int mod=1e5+3;
inl int read(){
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return x*f;
}
inl void write(int x){
    if(x<0){x=-x;putchar('-');}
    if(x>9)write(x/10);
    putchar(x%10+'0');
}
inl void writei(int x){write(x);putchar(' ');}
inl void writel(int x){write(x);putchar('\n');}
int n,c[N],u,v,res[N],rt[N];
int head[N],nxt[N],to[N],cnt;
inl void add(int u,int v){
    nxt[++cnt]=head[u];
    to[cnt]=v;
    head[u]=cnt;
}
struct seg_tree{
    int ans[N<<5],sum[N<<5],ls[N<<5],rs[N<<5],cnt;
    inl void pushup(int k){
        if(sum[ls[k]]>sum[rs[k]]){
            sum[k]=sum[ls[k]];
            ans[k]=ans[ls[k]];
        }else if(sum[ls[k]]<sum[rs[k]]){
            sum[k]=sum[rs[k]];
            ans[k]=ans[rs[k]];
        }else{
            sum[k]=sum[ls[k]];
            ans[k]=ans[ls[k]]+ans[rs[k]];
        }
    }
    inl void build(int &k,int l,int r,int x){
        k=++cnt,ans[k]=x,sum[k]=1;
        if(l==r)return;
        if(x<=mid)build(ls[k],l,mid,x);
        else build(rs[k],mid+1,r,x);
    }
    inl void merge(int &p,int q,int l,int r){
        if(!q)return;
        if(!p)return p=q,void();
        if(l==r)return sum[p]+=sum[q],void();
        merge(ls[p],ls[q],l,mid);
        merge(rs[p],rs[q],mid+1,r);
        pushup(p);
    }
}tree;
inl void dfs(int x,int fa){
    tree.build(rt[x],1,n,c[x]);
    for(int i=head[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa)continue;
        dfs(y,x);
        tree.merge(rt[x],rt[y],1,n);
    }
    res[x]=tree.ans[rt[x]];
}
signed main(){
    n=read();
    for(int i=1;i<=n;i++)c[i]=read();
    for(int i=1;i<=n-1;i++){
        u=read();v=read();
        add(u,v);add(v,u);
    }dfs(1,0);
    for(int i=1;i<=n;i++)writei(res[i]);
    return 0;
}

CF600F

题意：求二分图最小边染色方案

一个很好猜的结论：最小颜色数=点的最大度数

那么有一个比较显然的构造方案：分别找到一条边的两端点a,b最小的没染过的颜色ca,cb

如果这两个相同 那么直接染

如果不同 先强制染成ca 然而b点可能已经连着一条ca色的边了 那么可以像匈牙利算法一样 递归把之前的边颜色换成cb

由于是二分图 最后一定会剩下一个边颜色不冲突（tj这样说的 大概感性理解吧）

可以发现这样ca,cb一定不会超过最大点的度数

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
#define inl inline
#define mid (l+r>>1)
const int N=1e6+5;
const int M=2e3+5;
const int mod=1e5+3;
inl int read(){
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return x*f;
}
inl void write(int x){
    if(x<0){x=-x;putchar('-');}
    if(x>9)write(x/10);
    putchar(x%10+'0');
}
inl void writei(int x){write(x);putchar(' ');}
inl void writel(int x){write(x);putchar('\n');}
int a,b,m,to[M][M],qid[M][M],ans[N],x,y,ca,cb,ma;
inl void dfs(int x,int y,int ca,int cb){
    int p=to[y][ca];to[x][ca]=y;to[y][ca]=x;ans[qid[x][y]]=ca;
    if(!p)return to[y][cb]=0,void();
    dfs(y,p,cb,ca);
}
signed main(){
    a=read();b=read();m=read();
    for(int i=1;i<=m;i++){
        x=read();y=read()+a;
        qid[x][y]=qid[y][x]=i;
        ca=cb=1;
        while(to[x][ca])ca++;
        while(to[y][cb])cb++;
        if(ca==cb){
            ans[i]=ca;
            to[x][ca]=y;
            to[y][cb]=x;
            continue;
        }
        dfs(x,y,ca,cb);
    }
    for(int i=1;i<=m;i++)ma=max(ma,ans[i]);
    writel(ma);
    for(int i=1;i<=m;i++)writei(ans[i]);
    return 0;
}