二分图学习笔记
1.二分图判定
二分图定义:
一张图 \(G\) 是二分图当且仅当 \(G\) 的点集 \(V\) 可以分为两个点集 \(V_0,V_1\) ,满足 \(V_0∪V_1=V,V_0∩V_1=∅\)
且对于 \(G\) 的每条边 \(e\) ,其两个端点分别属于不同的点集。
通俗来讲就是 二分图中的点可以分成两个点集
在每个点集中没有边将他们直接联通 每条边的两个顶点都属于不同点集
二分图判定:
一张无向图是二分图:
当且仅当图中不存在奇环(奇环是指长度为奇数的环)
感性理解一下 我们用黑白两种颜色分别代表两个点集
那么对于一个奇环 我们如果按顺序把相邻的两点染成黑白 最后一定会剩一个点无法染色 非法
这就是染色法判定二分图
dfs版:
点击查看代码
int dfs(int x,int color){
if(col[x]){
if(col[x]^color)return 0;
return 1;
}
int flag=1;num[col[x]=color]++;
for(int i=head[x];i;i=nxt[i]){
int y=to[i];
flag&=dfs(y,color^1);
}
return flag;
}
bfs版:
点击查看代码
int bfs(int x){
queue<int>q;
q.push(x);num[col[x]=2]++;
while(!q.empty()){
int x=q.front();q.pop();
for(int i=head[x];i;i=nxt[i]){
int y=to[i];
if(col[y]){
if(col[y]^col[x])continue;
return 0;
}
num[col[y]=col[x]^1]++;q.push(y);
}
}
return 1;
}
2.二分图匹配
一张图的一个匹配是一些没有公共端点的边
显然对于一个二分图,一个匹配就是从一个点集向另一个连边 且一个点只连一条边或者不连
求二分图最大匹配算法:
1.匈牙利算法
主要思想就是 把左部点和右部点匹配 如果冲突(右部点被匹配过)
让原来与之匹配的左端点重新找
code:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define inl inline
#define pc putchar
const int N=5e2+5;
const int M=1e5+5;
const int inf=INT_MAX;
const int mod=9901;
inl int read(){
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
return x*f;
}
inl void write(int x){
if(x<0){pc('-');x=-x;}
if(x>9)write(x/10);
pc(x%10+'0');
}
inl void writel(int x){write(x);pc('\n');}
int n,m,u,v,e,vis[N][N],match[N],ask[N],ans;
bool dfs(int x){
for(int i=1;i<=m;i++){
if(!vis[x][i]||ask[i])continue;
ask[i]=1;
if(!match[i]||dfs(match[i])){
match[i]=x;return 1;
}
}
return 0;
}
inl void solve(){
for(int i=1;i<=n;i++){
memset(ask,0,sizeof(ask));
if(dfs(i))ans++;
}
}
signed main(){
n=read();m=read();e=read();
while(e--){
u=read();v=read();
vis[u][v]=1;
}
solve();
writel(ans);
return 0;
}
2.网络流dinic
在原图基础上建超级源点和汇点 先从源点连边到左部点 再从右部点连到汇点 直接跑dinic即可
比匈牙利算法更优
code:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define inl inline
#define pc putchar
const int N=2e5+5;
const int M=1e5+5;
const int inf=INT_MAX;
const int mod=9901;
inl int read(){
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
return x*f;
}
inl void write(int x){
if(x<0){pc('-');x=-x;}
if(x>9)write(x/10);
pc(x%10+'0');
}
inl void writel(int x){write(x);pc('\n');}
int n,m,e,u,v,s,t;
int head[N],nxt[N],to[N],w[N],cnt=1;
inl void add(int u,int v,int c){
nxt[++cnt]=head[u];to[cnt]=v;w[cnt]=c;head[u]=cnt;
nxt[++cnt]=head[v];to[cnt]=u;w[cnt]=0;head[v]=cnt;
}
queue<int>q;
int vis[N],dis[N],now[N];
int maxflow;
inl bool bfs(){
memset(vis,0,sizeof(vis));
memset(dis,0x3f,sizeof(dis));
memcpy(now,head,sizeof(now));
q.push(s);vis[s]=dis[s]=1;
while(!q.empty()){
int x=q.front();q.pop();vis[x]=0;
for(int i=head[x];i;i=nxt[i]){
int y=to[i],c=w[i];
if(c&&dis[y]>dis[x]+1){
dis[y]=dis[x]+1;
if(!vis[y]){q.push(y);vis[y]=1;}
}
}
}
return dis[t]<=1e5;
}
int dfs(int x,int flow){
if(x==t){maxflow+=flow;return flow;}
int rlow,used=0;
for(int i=now[x];i;i=now[x]=nxt[i]){
int y=to[i],c=w[i];
if(c&&dis[y]==dis[x]+1){
if(rlow=dfs(y,min(c,flow-used))){
used+=rlow;
w[i]-=rlow;
w[i^1]+=rlow;
if(used==flow)break;
}
}
}
return used;
}
inl int dinic(){
while(bfs())dfs(s,inf);
return maxflow;
}
signed main(){
n=read();m=read();e=read();
s=n+m+1,t=n+m+2;
for(int i=1;i<=n;i++)add(s,i,1);
for(int i=1;i<=m;i++)add(i+n,t,1);
for(int i=1;i<=e;i++){
u=read();v=read();
add(u,v+n,1);
}
writel(dinic());
return 0;
}
3.进阶补充内容
(upd 2023.12.25)
最小点覆盖
选最少的点,满足每条边至少有一个端点被选。
König 定理:二分图中,最小点覆盖 \(=\) 最大匹配。
考虑如下构造:
选择右侧未匹配的点,按照 “未匹配——匹配——未匹配......——未匹配——匹配” 的边找下去
(其实是最后没找到空节点的增广路)
让路径上所有点打上标记
都连完之后 答案即为 左侧打标记的点+右侧没打标记的点
证明:
简单画了个示意图:
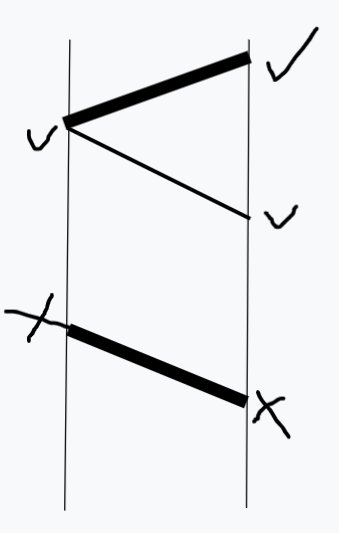
打√的是打标记,打×的是没标记
加粗的是匹配边,细的是非匹配边
证明该方案为一种点的覆盖:
按边种类分讨:
- 匹配边:
如图所示 该边无论是否选中 两侧端点打的标记一定相同 那么二者其一必然被选中 - 非匹配边:
只需要证明 左侧没打标记+右侧打了标记 不存在即可
根据构造方案 这时这条边一定被选中打标记 所以不存在
然后证数量为最大匹配数:
首先 显然每条匹配边两个点中必然只有一个点被选中 而且匹配边两两之间顶点均不同
那么这些点的数量就是最大匹配数
那么我们只要证非匹配边一段的选上的顶点是匹配边上的就行
讨论一下:
- 右端点被匹配:
1.右端点被打标记路径经过:该非匹配边左端点一定接了一条匹配边,否则就真成增广路了。
2.右端点没被打标记路径经过:右端点一定连着一条匹配边 否则就是标记路径起点了 - 右端点没被匹配:
一定为标记路径起点 一定依靠打了标记的左端点(一定有匹配边,否则这条边就匹配上了)
证毕。
证了一大堆,没看懂也无所谓,因为实际上没啥用。
最大独立集
选最多的点,满足两两之间没有边相连。
节选自oi-wiki:
因为在最小点覆盖中,任意一条边都被至少选了一个顶点,所以对于其点集的补集,任意一条边都被至多选了一个顶点,所以不存在边连接两个点集中的点,且该点集最大。因此二分图中,最大独立集和最小覆盖集互补。
最小路径覆盖
DAG最小不相交路径覆盖
把原图的每个点拆成 Ax 和 Ay 两个点,如果有一条有向边A->B,那么就加边Ax−>By。这样就得到了一个二分图。那么最小路径覆盖=原图的结点数-新图的最大匹配数。
感性理解:起始把 \(n\) 个点看做 \(n\) 条路径,连边当做合并两个路径。
每个点只能连一条入边和出边,即新图的最大匹配。
DAG最小可相交路径覆盖
用floyd求出原图的传递闭包,**对于任意A->B可达,都看做连边 A->B。
转化为了 DAG最小不相交路径覆盖 。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号