力扣HOT100
滑动窗口题目

滑动窗口
1 最长连续子字符串
-
题目
-
给定一个字符串
s,请你找出其中不含有重复字符的 最长子串 的长度。 -
思路 滑动窗口
使用 map 来存储当前已经遍历过的字符,key 为字符,value 为下标
使用 i 来标记无重复子串开始下标,j 为当前遍历字符下标
遍历字符串,判断当前字符是否已经在 map 中存在,存在则更新无重复子串开始下标 i 为相同字符的下一位置,此时从 i 到 j 为最新的无重复子串,更新 max ,将当前字符与下标放入 map 中
最后,返回 max 即可
法2
var lengthOfLongestSubstring = function(s) {
let map = new Map(), max = 0,i=0
for(let j = 0; j < s.length; j++) {
if(map.has(s[j])) {
i = Math.max(map.get(s[j]) + 1, i) //与之前i比较,因为左指针不能回头
}
map.set(s[j], j)
max = Math.max(max, j - i + 1)
}
return max
};
法一 没过
var lengthofLongestsubstring = function (s) {
let l=r=len=maxlen
let set=new Set()
while(r<s.length){
if(!set.has(s[r])){
set.add(s[r])
len++
r++
if(len>maxlen){
manxlen=len
}
}else{
while(set.has(s[r])){
set.delete(s[left])
len--
l++
}
set.add(s[r])
len++
r++
}
}
return maxlen;
}
动态规划
打家劫舍
两数相加
-
题目
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
-
思路
-
按位求和,进位
-
l1的长度>=l2的长度 l2的长度>l1的长度 末位需要/不需要进位
-
-
代码
var addTwoNumbers = function(l1, l2) {
let head1=l1,head2=l2
while(head1 !==null){
if(head2!=null){
head1.val+=head2.val //将l2的值加到l1上
head2=head2.next
}
//l1遍历完,l2还没有
if(head1.next==null&&head2!==null){
head1.next=head2
break //跳出当前循环
}
head1=head1.next
}
merge(l1)
return l1
};
function merge(head){ //遍历进位情况
while(head!=null){
if(head.val>=10){
head.val=head.val%10
if(head.next==null){
head.next=new ListNode(0) //需要进位
}
head.next.val+=1
}
head=head.next
}
}
合并两个有序链表
-
题目
-
思路
-
双指针
当 l1 和 l2 都不是空链表时,判断 l1 和 l2 哪一个链表的头节点的值更小,将较小值的节点添加到结果链表里,当一个节点被添加到结果里之后,将对应链表中的节点向后移一位。
在循环终止的时候, l1 和 l2 至多有一个是非空的。将非空链表接在合并链表的后面,并返回合并链表即可。
时间复杂度:O(n + m)
空间复杂度:O(1)
-
递归
当 l1 和 l2 都不是空链表时,判断 l1 和 l2 哪一个链表的头节点的值更小,将较小值的节点添加到结果链表里,当一个节点被添加到结果里之后,将对应链表中的节点向后移一位。
在循环终止的时候, l1 和 l2 至多有一个是非空的。将非空链表接在合并链表的后面,并返回合并链表即可。
时间复杂度:O(n + m)
空间复杂度:O(1)
-
-
代码
递归
var mergeTwoLists = function(l1, l2) {
if (l1 === null) {
return l2;
} else if (l2 === null) {
return l1;
} else if (l1.val < l2.val) {
l1.next = mergeTwoLists(l1.next, l2);
return l1;
} else {
l2.next = mergeTwoLists(l1, l2.next);
return l2;
}
};
迭代
var mergeTwoLists_2 = function(l1, l2) {
//不需要特意判断l1、l2为空
let head = new ListNode(0); //创建一个含有头结点的链表,随便指一个值,其第二个节点开始保存结果
let pre = head; //遍历结果的指针,总指向最后一个节点
while(l2 && l1){ //都不为null(空)时
if(l1.val > l2.val){ //l1对应的值大于l2
pre.next = l2;
l2 = l2.next; //l2往后遍历
}else{
pre.next = l1;
l1 = l1.next;
}
pre = pre.next; //pre更新
}
//将没有比较过的l1或者l2添加到尾部
pre.next = l1? l1: l2;//初始的时候不需要特意判断l1、l2为空,因为有一个为空会跳过while循环
return head.next; //头结点是新建的节点,返回时,不需要该点
最长回文字串
-
题目
给你一个字符串
s,找到s中最长的回文子串(正负读起来一样)。-
思路
-
中心扩展法
-
-
-
代码
var longestPalindrome = function(s) {
// 最长回文子串
var subString = "";
// 对于每个位置的子串寻找最长回文子串
for(let i=0; i<s.length; i++){
// 对于奇数串,返回每个位置的回文子串
var s1 = Palindrome(s,i,i);
// 对于偶数串,返回每个位置的回文子串
var s2 = Palindrome(s,i,i+1);
// 去检查每个位置的回文子串,找到那个最长的
if(s1.length > subString.length) subString = s1;
if(s2.length > subString.length) subString = s2;
}
// 通过这个函数去寻找以l、r为中心的回文子串
function Palindrome(s,l,r){
// 这是一个循环移动l、r两个指针的过程。当l和r指向的字符相同时,就继续分别向左和向右移动指针,直到不满足条件。
while(l >= 0 && r < s.length && s[l] == s[r]){
l--;
r++;
}
// 返回l到r之间的字符即可,这个部分就是这个位置的最长回文子串
return s.slice(l+1,r);
}
// 返回最长回文子串
return subString;
};
-
三数之和
-
题目
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
-
思路
-
排序+双指针法 模式识别:不可以包含重复,利用排序避免重复答案
-
思路:双指针法
1、如果数组中少于三个数直接返回空
2、对数组从小到大排序
3、第一个数遍历数组
4、第二个数为第一个数的下一个数,第三个数为数组最后一个数,第二个数小于第三个数时,判断三数和是否为0。为0则将这三个数放进数组,并将第一个数右移至下一个不重复的数重复判断,直到遍历完毕
-
-
代码
var threeSum = function(nums) {
const n = nums.length
const res = []
if(!nums || n < 3) return res
nums.sort((a,b)=>a-b)
for(let i = 0;i < n;i++){
if(i > 0 && nums[i] === nums[i-1]){ //排除重复的部分 升序
continue
}
let left = i + 1
let right = n - 1
while(left < right){
const sum = nums[i] + nums[left] + nums[right]
if(sum === 0){
res.push([nums[i], nums[left], nums[right]])
left++
//排除重复的部分 否则push了重复的三元组
//因为这里只移动left 所有只要判断left元素的是否重复
while(nums[left] === nums[left-1]){ //是while 不是if
left++
}
}else if(sum > 0){
right--
}else{
left++
}
}
}
return res
};-
复杂度
-
时间复杂度:O(n²)
空间复杂度:O(logn) 排序算法
-
-
环形链表Ⅱ
-
题目
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
-
思路
-
哈希表
-
时间复杂度:O(N),其中 N 为链表中节点的数目。我们恰好需要访问链表中的每一个节点。
空间复杂度:O(N),其中 N为链表中节点的数目。我们需要将链表中的每个节点都保存在哈希表当中。
-
-
快慢指针
-
如果有环,快慢指针一定相遇.当发现slow 与 fast 相遇时,我们再额外使用一个指针 ptr。起始,它指向链表头部;随后,它和slow 每次向后移动一个位置。最终,它们会在入环点相遇。
-
时间复杂度:O(N),其中 N 为链表中节点的数目。在最初判断快慢指针是否相遇时,slow 指针走过的距离不会超过链表的总长度;随后寻找入环点时,走过的距离也不会超过链表的总长度。因此,总的执行时间为 O(N)+O(N)=O(N)。
空间复杂度:O(1)。我们只使用了slow,fast,ptr 三个指针。
-
-
-
代码
哈希法
var detectCycle = function(head) {
const visited = new Set();
while (head !== null) {
if (visited.has(head)) {
return head;
}
visited.add(head);
head = head.next;
}
return null;
};
双指针法
var detectCycle = function(head) {
if (head === null) {
return null;
}
let slow = head, fast = head;
while (fast !== null) {
if (fast.next !== null) {
fast = fast.next.next;
slow = slow.next;
} else {
return null;
}
if (fast === slow) {
let ptr = head;
while (ptr !== slow) {
ptr = ptr.next;
slow = slow.next;
}
return ptr;
}
}
return null;
};
排序连表
-
题目
-
给你链表的头结点
head,请将其按 升序 排列并返回 排序后的链表 。 -
在
O(n log n)时间复杂度和常数级空间复杂度下,对链表进行排序
-
-
思路
-
代码
var sortList = function(head) {
// 去检验最后的拆分的节点,保证只有0个或者1个
if(!head || !head.next) return head;
// 1、找到链表的中间节点,拆分成左右两部分。并且将左右链表断开
let slow = head,fast = head; // 使用快慢指针找到中间节点
let preSlow = null; // 确定slow之前的节点,方便断链
while(fast && fast.next){
preSlow = slow;
slow = slow.next;
fast = fast.next.next;
}
// 断开左右链表,此时左链的头指针是head,右链的头指针是slow
preSlow.next = null;
// 2、将断开之后的左右链表再次断开,只到只有一个或者0个节点的左右链表。
const l = sortList(head);
const r = sortList(slow);
// 3、最后得到的左边一个节点l, 和右边一个节点r,两者进行排序合并。
return merge(l,r);
};
// 将链表进行合并,参考21题
var merge = function(l1,l2){
// 虚拟头节点
let dummyNode = new ListNode(-1);
let pre = dummyNode;
while(l1 && l2){
if(l1.val < l2.val){
pre.next = l1;
l1 = l1.next;
}else{
pre.next = l2;
l2 = l2.next;
}
pre = pre.next;
}
// 处理当某个链表为空的情况
if(l1) pre.next = l1;
if(l2) pre.next = l2;
return dummyNode.next;
}
回文子串
-
题目
-
思路
-
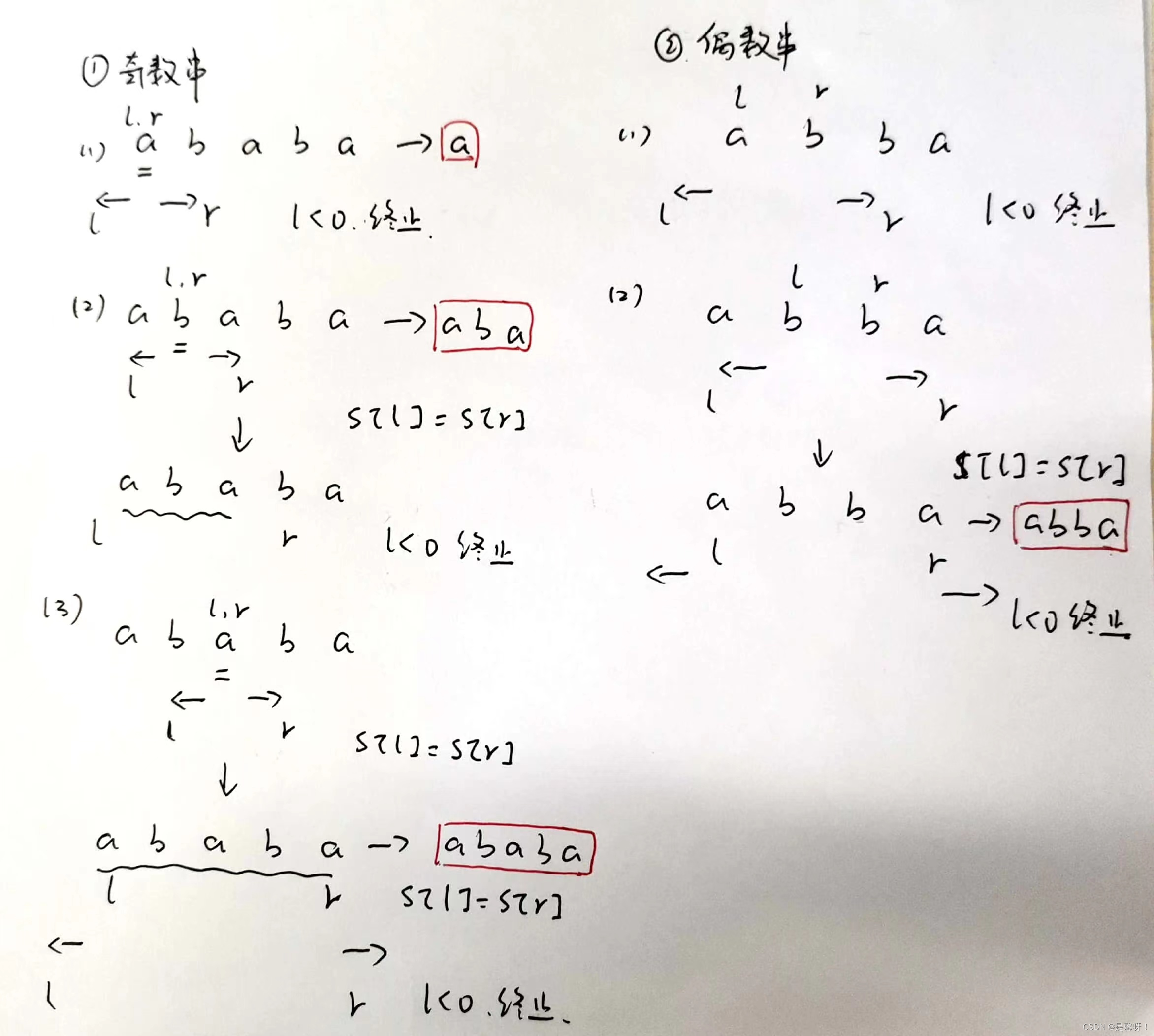
最长的区别在于,无论奇数偶数s,两个都过一遍,取最大。这个不行
-
长度为 nn 的字符串会生成 2n-1组回文中心[li,ri],其中li=i/2,ri=li+i mod 2
-
-
代码
var countSubstrings = function(s) {
const n = s.length;
let ans = 0;
for (let i = 0; i < 2 * n - 1; i++) {
let l = i / 2, r = i / 2 + i % 2;
while (l >= 0 && r < n && s.charAt(l) == s.charAt(r)) {
// 为什么不能用是s[l]=s[r]
l--;
r++;
ans++;
}
}
return ans;
};
最长回文子串
-
题目
-
对于一个子串而言,如果它是回文串,并且长度大于 22,那么将它首尾的两个字母去除之后,它仍然是个回文串。回文串”是一个正读和反读都一样的字符串
-
-
思路
-
中心扩散法
-
-
代码
var longestPalindrome = function(s) {
// 最长回文子串
var subString = "";
// 对于每个位置的子串寻找最长回文子串
for(let i=0; i<s.length; i++){
// 对于奇数串,返回每个位置的最长回文子串
var s1 = Palindrome(s,i,i);
// 对于偶数串,返回每个位置的最长回文子串
var s2 = Palindrome(s,i,i+1);
// 去检查每个位置的回文子串,找到那个最长的
if(s1.length > subString.length) subString = s1;
if(s2.length > subString.length) subString = s2;
}
// 通过这个函数去寻找以l、r为中心的回文子串
function Palindrome(s,l,r){
// 这是一个循环移动l、r两个指针的过程。当l和r指向的字符相同时,就继续分别向左和向右移动指针,直到不满足条件。
while(l >= 0 && r < s.length && s.charAt(l) == s.charAt(r)){
l--;
r++;
}
// 返回l到r之间的字符即可,这个部分就是这个位置的最长回文子串
return s.slice(l+1,r);
}
// 返回最长回文子串
return subString;
};
求二叉树最大宽度
二叉树的层序遍历
-
题目
-
思路
-
对比二叉树前序遍历,选取的数据结构是队,所以先进先出
-
主要多出部分,二叉树每一层放在一个数组里
-
et.push([]);
for (let i = 1; i <= currentLevelSize; i++) {
-
-
-
代码
-
var levelOrder = function(root) {
const ret = [];
if (!root) {
return ret;
}
const q = [];
q.push(root);
while (q.length !== 0) {
const currentLevelSize = q.length;
ret.push([]);
for (let i = 1; i <= currentLevelSize; ++i) { //此处不能直接i<=currentLevelSize 否则结果不准确
const node = q.shift();
ret[ret.length - 1].push(node.val);
if (node.left) q.push(node.left);
if (node.right) q.push(node.right);
}
}
return ret;
};
-
验证二叉搜索树
-
题目
-
思路
-
中序遍历 二叉搜索树「中序遍历」得到的值构成的序列一定是升序的
-
-
代码
-
var isValidBST = function(root) {
let stack = [];
let inorder = -Infinity;
while (stack.length || root !== null) {
while (root !== null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
// 如果中序遍历得到的节点的值小于等于前一个 inorder,说明不是二叉搜索树
if (root.val <= inorder) {
return false;
}
inorder = root.val;
root = root.right;
}
return true;
};
-
买卖股票的最佳时机(只进行一笔交易)
-
-
变量low表示当天前的最低点、res表示当天或者是当天之前交易能获得的最大利润, 每一天更新一次low和res
-
代码
var maxProfit = function(prices) {
let low = prices[0]
let res = 0
for (let i = 1; i < prices.length; i ++) {
low = Math.min(low, prices[i])
res = Math.max(res, prices[i] - low)
}
return res
};
-
-
贪心法
-
1、取最后一个元素作为最大值 2、从后往前遍历,如果大于最大值,就覆盖。否则就计算结果。 3、取结果中的最大值,即为最大利润。
-
var maxProfit = function(prices) {
const n = prices.length;
let result = 0;
// 取最后一个元素作为最大值
let max_price = prices[n-1];
// 从后往前遍历
for(let i=n-2;i>=0;i--){
if(prices[i] < max_price){
// 计算利润
result = Math.max(result,max_price-prices[i]);
}else{
max_price = prices[i];
}
}
return result;
};
-
交易次数不限
-
贪心:既然交易次数不限且可以当天卖出当天买入,那就只要能赚钱都去做这笔交易,就是说只要涨价,涨的价你都能赚到,把涨的价累加就可以了。
-
var maxProfit = function(prices) {
let res = 0
for (let i = 1; i < prices.length; i ++) {
if (prices[i] > prices[i - 1]) {
res += prices[i] - prices[i - 1]
}
}
return res
};
有效的括号
-
思路
栈保存左括号,遍历到右括号,查看栈顶元素是否为对应的右括号,是的话删除,不是false
为了快速判断括号的类型,使用哈希表存储每一种括号。哈希表的键为右括号,值为相同类型的左括号。
var isValid = function(s) {
const n = s.length;
if (n % 2 === 1) {
return false;
}
const pairs = new Map([
[')', '('],
[']', '['],
['}', '{']
]);
const stk = [];
for (let ch of s){
if (pairs.has(ch)) {
if (stk.length==0 || stk[stk.length - 1] !== pairs.get(ch)) {
return false;
}
stk.pop();
}
else {
stk.push(ch);
}
};
return stk.length==0;
};
移动0
-
题目
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
-
代码
-
splice+push
-
function moveZeroes(arr) {
let count = 0; //用count来防止死循环
for (let i = 0; i < arr.length - count; i++) {
while (arr[i] === 0) { //一直对i=1判断,直到它的值不是0 //优先遍历完while循环 ,拿到最终的count 跳出for循环换。不能用if,if只能取到当前count. 反例【0,0,1】
arr.splice(i, 1);
arr.push(0);
count++;
}
}
return arr;
}
-
快慢指针
var moveZeroes = function (nums) {
var n = nums.length
var k = 0//慢指针
for (let i = 0; i < n; i++) {
if (nums[i] != 0) {
nums[k] = nums[i]//k从头慢慢放不为0的数
k++
}
}
for (let i = k; i < n; i++) {
nums[i] = 0 //剩下的置为0
}
return nums
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号