WZU_校赛补题

2025 WZU校赛补题

A.奖金发放

题面描述

温州大学第十八届“小橙教育杯”大学生程序设计竞赛的奖金是特等奖480元/队，一等奖240元/队，二等奖120元/队，三等奖60元/队，最佳女队奖120元/队。按评奖规定，特等奖1队（可能空缺），一等奖10队或8%有效参赛队数（以少者为准，下同），二等奖20队或16%有效参赛队数，三等奖30队或24%有效参赛队数，最佳女队奖1队（可能空缺）。如果有效队数已知，获奖队数按四舍五入计算。问奖金发放总额最多是多少，最少又是多少？

输入格式:

先输入整数t，表示问题个数。然后输入t个整数，表示有效参赛队数。

输出格式:

对每个问题，在一行内输出奖金发放总额的最大值和最小值，用一个空格隔开。所有数据都不会超过int型变量的范围。

输入样例:

3
107
58
148

输出样例:

6360 5760
3720 3120
7200 6600

AC code:

void solve(){
    int n;cin>>n;
    int num1=min((int)round((double)n*0.08),10);
    int num2=min((int)round((double)n*0.16),20);
    int num3=min((int)round((double)n*0.24),30);
    int ans=num1*240+num2*120+num3*60;
    cout<<ans+600<<' '<<ans<<endl;
}

B.Hole Enthusiast

题面描述

A hole enthusiast ACMer has a peculiar habit: whenever he
sees a number, he can't help but count the number of "holes" in it. The digit 0 has one hole, 1, 2, 3, 4, 5, and 7 have no holes, 6 and 9 have one hole, and 8 has two holes. Therefore, the total number of holes in a number is the sum of the holes in each of its digits. For example, the number 68530 has a
total of 4 holes.

Input:

The first line contains an integer T(1≤T≤10), representing the number of test cases. Each test case contains a non-negative
integer n(0≤n≤2×10⁹ ), without leading zeros.

Output:

For each test case, output a single line containing the total number of holes in the number.

Sample Input:

3
68530
4517
108

Sample Output:

4
0
3

AC code:

map<char,int>mp={{'0',1},{'6',1},{'8',2},{'9',1}};
void solve(){
    string s;cin>>s;
    ll ans=0;
    for(int i=0;i<s.size();i++) ans+=mp[s[i]];
    cout<<ans<<endl;
}

C.江滨路对岸的风景(1)

题面描述

江滨路对岸绿水青山，风景优美。漫步也好、骑行也罢，抑或驱车，美不胜收的景色让人心旷神怡。可是城市规划与建设出了点问题，商家、机构、私人会所纷纷在江滨路的水岸一侧违章修建了各种建筑物，美其名曰“江景轩”“水岸生活”“岸芷汀兰”，挡住了江滨路上观光客眺望对岸的视线。

设想江滨路是直线上分布的一系列整数格点{1,2,⋯,n}，违章建筑是一个整数线段[a_i,b_i](1≤ a_i≤b_i≤n,i=1,⋯,m)，表示遮挡了江滨路上的一段连续的整数格点a_i,a_i+1,⋯,b_i
。有q个观光客，每个观光客从江滨路的s_j​ 格点步行（骑行或驱车）到t j​ 格点(1≤s_j​≤t_j​≤n，j=1,⋯,q)，问每个观光客能看到多少对岸的风景，即路段[s_j​,t_j​]风景没被遮挡的格点数是多少。

输入格式:

先输入n,m和q，分别表示违章建筑数量和观光客人数。(1≤n,m,q≤1000)

然后输入2m个整数a₁,b₁,a₂,b₂,⋯,a_m,b_m，表示各个建筑物线段。(1≤a_i≤b_i≤n)然后输入2q个整数s₁,t₁,s₂,t₂,⋯,s_q,t_q，表示各个观光客的观光路段。(1≤s_j≤t_j≤n)

输出格式:

对于每个询问，输出一行整数，表示能看见的风景长度（没被遮挡的格点数）。

输入样例:

12 5 3
1 5 4 6 9 9 1 2 8 10
1 12 2 9 5 5

输出样例:

3
1
0

AC code:

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
int main(){
    cin.tie(0)->ios::sync_with_stdio(false);
    int n,m,q;    
    cin>>n>>m>>q;    
    vector<int>a(n+1);
    for(int i=1,x,y;i<=m;i++) {
        cin>>x>>y;
        for(int j=x;j<=y;j++) a[j]=1;
    }
    for(int i=1,x,y;i<=q;i++){
        ll ans=0;
        cin>>x>>y;
        for(int j=x;j<=y;j++) if(!a[j]) ans++;
        cout<<ans<<endl;
    }
    return 0;
}

D.栅格填数

题面描述

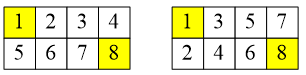
栅格填数在计算机图形显示中有很多应用。填数方式有两种，设要填的范围是一个N行M列的矩阵。一种填法是填完上一行再填下一行，每个从左往右填，依次填入从1开始的连续整数，一直到N×M。另一种填法是填完左列再填右列，每列从上往下，依次填入从1开始的连续整数。
例如：当N=2,M=4，栅格的两种填数结果是

两种填法在同一位置数字相同的栅格已用黄色标出，共有2个。对任意的正整数N,M，数字相同的栅格有几个呢？

输入格式:

第一行输入问题整数T，表示问题的个数。接下来T行，每行输入两个整数N和M，表示矩阵的行数和列数。
(T≤1000, 1≤N,M≤2×10⁹)

输出格式:

输出T行，为每个问题的答案，即两种填法数字相同的栅格数。

输入样例:

1
2 4

输出样例:

2

解题思路:

注意到,a_ij=n*(i-1)+j,而b_ij=i+(j-1)*m,要找到两矩阵重复元素出现个数,就要求a_ij=b_ij的个数,尝试化简式子
n*(i-1)+j=i+(j-1)*m
i*(n-1)-n=j*(m-1)-m
i*(n-1)-n-1=j*(m-1)-m-1
(i-1)*(n-1)=(j-1)*(m-1)
即求(i-1)/(j-1)=(m-1)/(n-1)满足这样条件的ij个数,求最大公约数就可以啦

AC code:

void solve(){
    int n,m;cin>>n>>m;
    cout<<__gcd(n-1,m-1)+1<<endl;
}

E.多多益善

题面描述

我也想编个好的故事给你们当题目，可是并没这能力。直接说我的意思吧。
有很多好东西，让你拣，你最多只能拣走总重量W的东西，每样东西的重量和价值都是已知的。对单件东西，你也可以掰一部分来，掰来a%，价值也是它的a%。问你拣的总价值最多达到多少。

输入格式:

输入好东西的个数n，以及总重量W。再输入2n个正整数，w₁ ,v₁​,w₂,v₂ ,⋯,w_n,v_n ，分别是每个东西的重量和价值。1≤n≤w≤10⁵。0<v_i,w_i<=10⁴ 。

输出格式:

对每个问题，在一行内输出奖金发放总额的最大值和最小值，用一个空格隔开。所有数据都不会超过int型变量的范围。

输入样例:

3 10
10 14
2 5
4 1

输出样例:

16.200

AC code:

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
const int N=2e5+10;
struct node{
    int a,b;
    double c;
    friend bool operator<(node a,node b){
        return a.c>b.c;
    }
}a[N];
int main(){
    cin.tie(0)->ios::sync_with_stdio(false);
    int n,w;cin>>n>>w;
    for(int i=1;i<=n;i++) cin>>a[i].a>>a[i].b,a[i].c=(double)a[i].b/a[i].a;
    sort(a+1,a+1+n);
    double ans=0;
    for(int i=1;i<=n&&w>0;){
        ans+=a[i].c;
        a[i].a--;
        w--;
        if(!a[i].a) i++;
    }
    cout<<fixed<<setprecision(3)<<ans<<endl;
    return 0;
}

F.整数K分解

题面描述

给定两个正整数N,K，问能否把N表示成恰好K个3^m形式（m是非负整数）的整数之和？

输入格式:

第一行输入问题个数T。接下来T行，每行输入两个整数N和K。(0<N,K≤10⁹)

输出格式:

输出T行，对于每个问题，如果可以输出 Yes，否则输出No。

输入样例:

2
5 3
4 3

输出样例:

Yes
No

解题思路:

注意到,K最大取值是n,最小取值是K的三进制中1的个数,三进制满足每三位可以进一位,那么
有K的取值可以为n,n-2,n-4,n-6...x(x是k的三进制中1的个数),
因此只需判断n与k的奇偶性并判断k是否在最小与最大区间中

AC code:

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
ll q_pow(int x){
    ll s=1;
    while(x){
        if(x&1){
            s=(s<<1)+s;
        }
        x>>=1;
    }
    return s;
}//3次幂计算
void solve(){
    ll n,k;cin>>n>>k;
    int Min=0,Max=n;
    int i=0;
    auto pren(n);
    while(n){
        i=0;
        while(q_pow(i)<=n) i++;
        i--;
        n-=q_pow(i);
        Min++;
    }
    cout<<((k>=Min&&k<=Max&&(pren-k)%2==0)?"Yes":"No")<<endl;
}
int main(){
    cin.tie(0)->ios::sync_with_stdio(false);
    int T;cin>>T;
    while(T--) solve();
    return 0;
}

J.丁税第五版

题面描述

作为一国之大司徒，制定一套丁税（面向个人的税收）方案责无旁贷。大司徒在推出前四版方案之后，仍觉不甚完美。他发现数据的“连续度”既可操作又极具识别性，决定以此确定税基。户部提供的数据是一个大小为n的正整数序列a₁, a₂,⋯,a_n​ ，而每个臣民具有两个表示身份的数s,t(1≤s,t≤n)，他的税基就是子段a s ,⋯,a t 的连续度，即子段元素上下限之间没有出现的整数个数除以该子段的元素跨度。例如子段是(8, 2, 5, 2, 3)，最小元是2，最大元是8，2~8跨度为7，其中没有出现的数字是4,6,7，共3个，所以税基为3/7。特别地，如果s=t，税基是0，表示特权臣民。
但是问题又来了，大批臣民只知道自己的s,t，于是纷纷来询问自己的税基。大司徒面对一大批臣民的询问，需要逐一回答。

输入格式:

先输入n,m，分别表示序列a的长度和询问次数。然后输入n个整数，表示序列元素a_i 。最后输入2m个整数s_i,t_i (1≤s_i≤t _i≤n)，表示臣民的身份数字。(1≤n,m≤50000,1≤a_i≤50000)

输出格式:

对每次询问，输出臣民关心的税基，用最简分数格式（如3/7），独占一行。

输入样例:

10 4
5 3 5 5 4 2 2
4 8 2
1 8
7 10
2 5
1 3

输出样例:

0/1
4/7
0/1
1/3

解题思路:

本题是离线询问区间最值和在区间中元素种类的变式，离线询问区间最值直接st表就行了，喜欢莫队和树状数组的小朋友一眼就能看出来做法。
ps:如果强制在线可能会很麻烦，偶没学过。

AC code1(莫队):

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
const int N=2e5+10;
int a[20][N],b[20][N];
ll ans;
int cnt[N];
struct Q{
    int l,r,id,pos;
    friend bool operator<(Q a,Q b){
        return (a.pos==b.pos)?((a.pos&1)?(a.r<b.r):(a.r>b.r)):(a.l<b.l);
    }
}q[N];
int querymin(const int &l,const int &r){
    int len=__lg(r-l+1);
    return min(b[len][l],b[len][r-(1<<len)+1]);
}
int querymax(const int &l,const int &r){
    int len=__lg(r-l+1);
    return max(a[len][l],a[len][r-(1<<len)+1]);
}
void add(int x){
    int y=a[0][x];
    if(cnt[y]==0) ans++;
    cnt[y]++;
}
void sub(int x){
    int y=a[0][x];
    cnt[y]--;
    if(cnt[y]==0) ans--;
}
int main(){
    cin.tie(0)->ios::sync_with_stdio(false);
    int n,m;cin>>n>>m;
    int siz=sqrt(n+0.5);
    for(int i=1;i<=n;i++) cin>>a[0][i],b[0][i]=a[0][i];
    int len=__lg(n);
    for(int i=1;i<=len;i++){
        for(int j=1;j<=n-(1<<i)+1;j++){
            a[i][j]=max(a[i-1][j],a[i-1][j+(1<<i-1)]);
            b[i][j]=min(b[i-1][j],b[i-1][j+(1<<i-1)]);
        }
    }
    vector<pair<int,int>>res(m+1);
    for(int i=1,l,r;i<=m;i++){
        cin>>q[i].l>>q[i].r;
        q[i].id=i;
        q[i].pos=(q[i].l-1)/siz;
        res[i].second=querymax(q[i].l,q[i].r)-querymin(q[i].l,q[i].r)+1;
    }
    sort(q+1,q+1+m);
    int l=1,r=0;//经典左闭右闭写法
    for(int i=1;i<=m;i++){
        while(l>q[i].l) add(--l);
        while(r<q[i].r) add(++r);
        while(l<q[i].l) sub(l++);
        while(r>q[i].r) sub(r--);
        res[q[i].id].first=res[q[i].id].second-ans;
    }
    for(int i=1;i<=m;i++){
        if(res[i].first==0||res[i].second==0) res[i]={0,1};
        else {
            int base=__gcd(res[i].first,res[i].second);
            res[i].first/=base,res[i].second/=base;
        }
        cout<<res[i].first<<'/'<<res[i].second<<endl;
    }
    return 0;
}
//离线莫队维护区间可重性

AC code2(树状数组):

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
const int N=2e5+10;
struct Q{
    int l,idx;
};
int n,m;
int a[20][N],b[20][N],tree[N*2];
inline int lowbits(const int &x){ return x&-x; }
void add(int x,const int &k){
    while(x<=n){
        tree[x]+=k;
        x+=lowbits(x);
    }
}
int sum(int x){
    int ans=0;
    while(x){
        ans+=tree[x];
        x&=x-1;
    }
    return ans;
}
void init(){
    int len=__lg(n);
    for(int i=1;i<=len;i++){
        for(int j=1;j<=n-(1<<i)+1;j++){
            a[i][j]=max(a[i-1][j],a[i-1][j+(1<<i-1)]);
            b[i][j]=min(b[i-1][j],b[i-1][j+(1<<i-1)]);
        }
    }
}
int q_min(const int &l,const int &r){
    int len=__lg(r-l+1);
    return min(b[len][l],b[len][r-(1<<len)+1]);
}
int q_max(const int &l,const int &r){
    int len=__lg(r-l+1);
    return max(a[len][l],a[len][r-(1<<len)+1]);
}
int main(){
    cin.tie(0)->ios::sync_with_stdio(false);
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[0][i],b[0][i]=a[0][i];
    init();
    vector<vector<Q>>query(n+1);
    for(int i=0,l,r;i<m;i++){
        cin>>l>>r;
        query[r].push_back(Q{l,i});
    }
    map<int,int>las;//每个元素最后出现的位置
    vector<pair<int,int>>res(m);
    for(int r=1;r<=n;r++){
        if(las.count(a[0][r])){
            add(las[a[0][r]],-1);
        }
        add(r,1);
        las[a[0][r]]=r;
        for(auto &q:query[r]){
            auto [l,idx]=q;
            int fenmu=q_max(l,r)-q_min(l,r)+1;
            int fenzi=fenmu-(sum(r)-sum(l-1));

            int base=__gcd(fenzi,fenmu);
            if(base==0) base=1,fenmu=1;
            fenzi/=base,fenmu/=base;
            res[idx]={fenzi,fenmu};
        }
    }
    for(auto &[x,y]:res){
        cout<<x<<'/'<<y<<endl;
    }
    return 0;
}