前缀和经典问题整理

1、一般形式  --  区域和检索 - 数组不可变

class NumArray:

    def __init__(self, nums: List[int]):
        self.pre = [0]
        for num in nums:
            self.pre.append(self.pre[-1] + num)
        ####或者#####
        self.pre = list(accumulate(nums, initial=0))

    def sumRange(self, left: int, right: int) -> int:
        return self.pre[right + 1] - self.pre[left]

2、经典问题 --  连续数组

给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组，并返回该子数组的长度。

class Solution:
    def findMaxLength(self, nums: List[int]) -> int:
        pre, m = 0, {0: -1}
        maxl = 0
        for i, num in enumerate(nums):
            pre += 1 if num == 1 else -1
            if m.get(pre, None) != None:
                maxl = max(i - m[pre], maxl)
            else:
                m[pre] = i
        return maxl

前后缀 -- 除自身以外数组的乘积

class Solution:
    def productExceptSelf(self, nums: List[int]) -> List[int]:
        right = [1] * (len(nums) + 1)
        for i in reversed(range(len(nums))):           
            right[i] = right[i + 1] * nums[i]

        left = 1
        res = [1] * (len(nums))
        for i in range(len(nums)):
            res[i] = left * right[i + 1]
            left *= nums[i]
        return res

前缀异或 -- 形成两个异或相等数组的三元组数目

class Solution:
    def countTriplets(self, arr: List[int]) -> int:
        n = len(arr)
        s = [0]
        for val in arr:
            s.append(s[-1] ^ val)
        
        cnt, total = Counter(), Counter()
        ans = 0
        for k in range(n):
            if s[k + 1] in cnt:
                ans += cnt[s[k + 1]] * k - total[s[k + 1]]
            cnt[s[k]] += 1
            total[s[k]] += k

        return ans

求一个数组两两乘积之和

res, s = 0, sum(nums)
for num in nums:
    s -= num
    res += s * num
return res

类似的有 -- 统计梯形的数目 I

class Solution:
    def countTrapezoids(self, points: List[List[int]]) -> int:
        m = defaultdict(int)
        for x, y in points:
            m[y] += 1
        res = 0
        arr = list(m.keys())
        pre = 0
        for i in range(len(arr)):
            pre = (pre + m[arr[i]]  * (m[arr[i]] - 1) // 2) % (10 ** 9 + 7)
        
        for i in range(len(arr)):
            pre = (pre - m[arr[i]]  * (m[arr[i]] - 1) // 2) % (10 ** 9 + 7)    
            a2 = m[arr[i]]  * (m[arr[i]] - 1) // 2 % (10 ** 9 + 7)
            res = (res + a2 * pre) % (10 ** 9 + 7)
        return res

枚举分母，对商进行前缀求和 --  向下取整数对和　

class Solution:
    def sumOfFlooredPairs(self, nums: List[int]) -> int:
        m = Counter(nums)
        maxl = max(nums)
        pre = [0] * (maxl + 1)
        for i in range(1, maxl + 1):
            pre[i] = pre[i - 1] + m[i]
        res = 0
        for num in m:
            i = 1
            while i * num <= maxl:
                if maxl < (i + 1) * num - 1:
                    res = (res + (pre[-1] - pre[i * num - 1]) * i * m[num]) % (10 ** 9 + 7)
                else:
                    res = (res + (pre[(i + 1) * num - 1] - pre[i * num - 1]) * i * m[num]) % (10 ** 9 + 7)
                i += 1 
        return res

前缀最值 -- 有序三元组中的最大值 II

class Solution:
    def maximumTripletValue(self, nums: List[int]) -> int:
        n = len(nums)
        right = [0] * (n + 1)
        i = n - 1
        for num in reversed(nums):
            right[i] = max(right[i + 1],  num)
            i -= 1

        left, maxl = 0, 0
        for i, num in enumerate(nums):
            maxl = max(maxl, (left - num) * right[i + 1])
            left = max(left, num)
        return maxl

3、二维数组前缀和和差分

（1）二维数组前缀和 -- 二维区域和检索 - 矩阵不可变

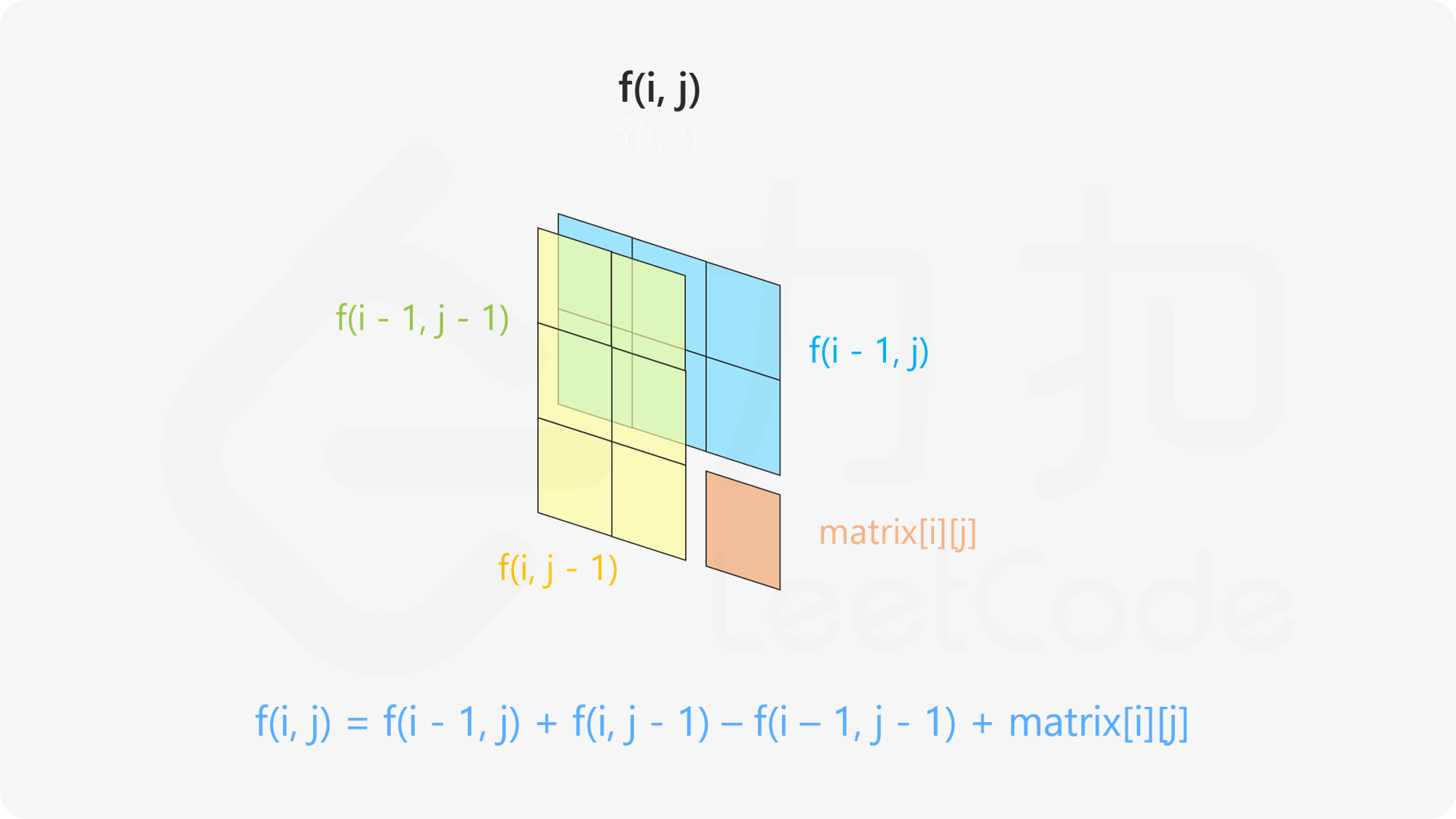
 代码：

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        self.sum_matrix = [[0] * len(matrix[0]) for _ in matrix]
        for i in range(len(matrix)):
            row_sum = 0
            for j in range(len(matrix[i])):
                row_sum += matrix[i][j]
                self.sum_matrix[i][j] = self.sum_matrix[i - 1][j] + row_sum

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        res = self.sum_matrix[row2][col2]
        if col1 > 0: res -= self.sum_matrix[row2][col1 - 1]
        if row1 > 0: res -= self.sum_matrix[row1 - 1][col2]
        if col1 > 0 and row1 > 0: res += self.sum_matrix[row1 - 1][col1 - 1]
        return res

（2）二维数组差分 -- 子矩阵元素加 1

class Solution:
    def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:
        d = [[0] * (n + 1) for _ in range(n + 1)]
        for r1, c1, r2, c2 in queries:
            d[r1][c1] += 1
            d[r2 + 1][c2 + 1] += 1
            d[r1][c2 + 1] -= 1
            d[r2 + 1][c1] -= 1
        
        ans = [[0] * (n + 1) for _ in range(n + 1)]
        for i, row in enumerate(d[:n]):
            for j, x in enumerate(row[:n]):
                ans[i + 1][j + 1] = ans[i + 1][j] + ans[i][j + 1] - ans[i][j] + x
        del ans[0]
        for row in ans:
            del row[0]
        return ans

数组差分可以看成函数微分，数组前缀和可以看成函数积分，所以差分数组的前缀和就是原数组

4、字符串哈希 + 前缀和 -- 不同的循环子字符串

class Solution:
    def distinctEchoSubstrings(self, text: str) -> int:
        n = len(text)
        mod, base = 10**9 + 7, 31
        pre, mul = [0] * (n + 1), [1] + [0] * n
        for i in range(1, n + 1):
            pre[i] = (pre[i - 1] * base + ord(text[i - 1])) % mod
            mul[i] = mul[i - 1] * base % mod

        def get_hash(l, r):
            return (pre[r + 1] - pre[l] * mul[r - l + 1] % mod + mod) % mod

        seen = {x: set() for x in range(n)}
        ans = 0
        for i in range(n):
            for j in range(i + 1, n):
                l = j - i
                if j + l <= n:
                    hash_left = get_hash(i, j - 1)                   
                    if hash_left not in seen[l - 1] and hash_left == get_hash(j, j + l - 1):
                        ans += 1
                        seen[l - 1].add(hash_left)
        return ans

　5、进阶问题

（1）个数前缀和 -- 查询差绝对值的最小值

class Solution:
    def minDifference(self, nums: List[int], queries: List[List[int]]) -> List[int]:
        pre = [[0] for _ in range(101)]
        for n in nums:
            for i in range(101):
                if i == n:
                    pre[i].append(pre[i][-1] + 1)
                else:
                    pre[i].append(pre[i][-1])
        res = []
        for f, t in queries:
            last, minl = None, inf
            for i in range(101):
                if pre[i][t + 1] - pre[i][f] > 0:
                    if last is not None:
                        minl = min(i - last, minl)
                    last = i
            res.append(minl if minl != inf else -1)
        return res

（2）统计回文子序列数目

class Solution:
    def countPalindromes(self, s: str) -> int:
        suf = [0] * 10
        suf2 = [0] * 100
        for d in map(int, reversed(s)):
            for j, c in enumerate(suf):
                suf2[d * 10 + j] += c
            suf[d] += 1

        ans = 0
        pre = [0] * 10
        pre2 = [0] * 100
        for d in map(int, s):
            suf[d] -= 1
            for j, c in enumerate(suf):
                suf2[d * 10 + j] -= c  # 撤销
            ans += sum(c1 * c2 for c1, c2 in zip(pre2, suf2))  # 枚举所有字符组合
            for j, c in enumerate(pre):
                pre2[d * 10 + j] += c
            pre[d] += 1
        return ans % (10 ** 9 + 7)

（3）统计上升四元组

class Solution:
    def countQuadruplets(self, nums: List[int]) -> int:
        n = len(nums)
        more = [[0] * n for _ in range(n + 1)]
        less = [[0] * n for _ in range(n + 1)]
        for j in reversed(range(n)):
            for k in reversed(range(j + 1, n)):
                if nums[j] < nums[k]:
                    more[k][j] = more[k + 1][j] + 1
                else:
                    more[k][j] = more[k + 1][j]

        for k in range(n):
            for j in range(k):
                if nums[k] > nums[j]:
                    less[j][k] = less[j - 1][k] + 1
                else:
                    less[j][k] = less[j - 1][k]
        
        res = 0
        for k in range(n):
            for j in range(k):
                if nums[k] < nums[j]:
                    res += less[j][k] * more[k][j]
        
        return res

 (4)前缀和 + 哈希 + 同余 -- 统计美丽子字符串 II

class Solution:
    def beautifulSubstrings(self, s: str, k: int) -> int:
        k = self.sqrt(k * 4)
        cnt = Counter([(0, 0)])  
        ans = pre_sum = 0
        for i, c in enumerate(s):
            pre_sum += 1 if c in "aeiou" else -1
            p = ((i + 1) % k, pre_sum)
            ans += cnt[p]
            cnt[p] += 1
        return ans

    def sqrt(self, n: int) -> int:
        res = 1
        i = 2
        while i * i <= n:
            i2 = i * i
            while n % i2 == 0:
                res *= i
                n //= i2
            if n % i == 0:
                res *= i
                n //= i
            i += 1
        if n > 1:
            res *= n
        return res

（5）二维矩阵压缩到一维 + 前缀和 + 哈希 -- 矩形区域不超过 K 的最大数值和

class Solution:
    def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:
        m, n = len(matrix), len(matrix[0])
        res = 0
        for i in range(1, n + 1):
            presum = [0] * (m + 1)
            for j in range(i, n + 1):
                a = 0
                d = defaultdict(int, {0:1})
                for fixed in range(1, m + 1):
                    presum[fixed] += matrix[fixed-1][j-1]
                    a += presum[fixed]
                    res += d[a - target]
                    d[a] += 1
        return res