第九篇:向量导数
向量的导数

向量求导及证明
向量求导其本质和标量求导没有本质区别。
本文所有的公式推导其根本立足于以下公式:
本文所描述的公式均以公式作为证明基础。但在证明之前,首先明确一个概念,即所谓布局。
布局
布局在很多博客上都有不同的定义,比如某个博客定义如下:
分子布局(Numerator-layout): 分子为 y 或者分母为 xT (即,分子为列向量或者分母为行向量)
分母布局(Denominator-layout): 分子为 yT 或者分母为 x (即,分子为行向量或者分母为列向量)
我个人认为,布局本质上讲是一种规定,用以规定在运算过程中的描述方法,因为不同的描述方法可能存在不同。而与具体的分子分母如何关系不大。用我们定义的公式来说,我们公式定义的情况是传统认为的分子布局,而分母布局则是将公式中
和
的排布反过来,相当于做一次转置(这也解释了为什么分子布局和分母布局的结果正好差一个转置)。
公式推导
公式1
假设
其中和
形状分别为
和
,
是一个规模为
的矩阵,且和
线性无关。这是我们的基础定义,后续公式如果不特别说明则沿用此定义。
则有:
证明:
对于的第
个元素
,有:
因此可得:
则推广到所有的元素,易得
公式2
假设
其中和
形状分别为
和
,
是一个规模为
的矩阵,且和
线性无关。如果
与
有函数关系,那么则有:
证明:
对于的第
个元素
,有:
因此可得:
则推广到所有的元素,易证(事实上这跟标量求导里面的链式法则没什么区别)。
公式3
假设
其中和
形状分别为
和
,
是一个规模为
的矩阵,且和
、
线性无关。那么则有:
证明:
定义
则
因此可得:
另一公式使用相似方法可证,只需要对进行一次转置(标量的转置扔为自身)。
公式4(公式3特殊情况)
假设
其中形状分别为
,
是一个规模为
的矩阵,且和
线性无关。那么则有:
证明:
根据定义:
则可以得到:
推广到所有元素可得结论。
公式5(公式4特殊情况)
假设
其中形状分别为
,
是一个规模为
的矩阵,且和
线性无关,并且还是一个对称矩阵。那么则有:
证明:
这根本不需要证
公式6
假设
其中和
形状分别为
和
,并且均为向量
的函数结果。那么则有:
证明:
还是标量求导法则的推广。
公式7(公式6的特殊情况)
假设
其中和
形状分别为
和
,并且均为向量
的函数结果。那么则有:
证明:
还是标量求导法则的推广。
公式8
假设
其中和
形状分别为
和
,并且均为向量
的函数结果。那么则有:
证明:
参考公式3证明即可。
公式9(公式8特殊情况)
假设
其中形状为
,并且为向量
的函数结果。那么则有:
证明:
不需要证
公式10(公式9特殊情况)
假设
其中形状为
,并且为向量
的函数结果。并且A是对称的。那么则有:
证明:
不需要证。
公式11或者称为定义(矩阵求导)
设规模为
,
为一个标量,那么:
公式12
向量的导数公式

标量对向量的导数


from sympy import pprint,Symbol,linsolve,solve,symarray,Eq,Expr,roots,diff from sympy.matrices import Matrix,zeros,diag,eye from sympy.abc import lamda def mySyms(prefix,shape,**kwargs): from numpy import empty, ndindex arr = empty(shape, dtype=object) for index in ndindex(shape): arr[index] = Symbol('%s_%s' % (prefix, ''.join(map(str, index))), **kwargs) return arr A = Matrix(mySyms('a',(6,6),real=True)) A.col_del(0) A.row_del(0) X = Matrix(symarray('x',5)) print('A矩阵:') pprint(A) Y = A*X def vet_diff(Y:Matrix,X): df_m = Matrix() for f in Y: res_list = [] for x in X: res_list.append(diff(f,x)) # df_m.append(res_list) df_m = df_m.row_join(Matrix(res_list)) if X.shape[1] > X.shape[0]: return df_m.T return df_m print('A*X对向量X求导:') pprint(vet_diff(Y,X)) print() print('A*X对向量X的转置求导:') pprint(vet_diff(Y,X.T)) print() print('X.T*A对向量X求导:') pprint(vet_diff(X.T*A,X)) print('X.T*A*X对向量X求导:') #为了计算效率用实数矩阵 B = Matrix([[0,2,3,1,2],[4,0,7,5,6],[7,3,5,8,9],[3,8,9,4,1],[5,4,3,9,7]]) dB = vet_diff(X.T*B*X,X) pprint(dB.shape) print('(A.T+A).inv():') print((B.T+B).inv()) # pprint(((B.T+B).inv()).row(0)*dB) print('(A.T+A).inv()*X.T*A*X对向量X的导数') pprint((B.T+B).inv()*dB)
标量对方阵的导数

from sympy import pprint,Symbol,linsolve,solve,symarray,Eq,Expr,roots,diff from sympy.matrices import Matrix,zeros,diag,eye from sympy.abc import lamda def mySyms(prefix,shape,**kwargs): from numpy import empty, ndindex arr = empty(shape, dtype=object) for index in ndindex(shape): arr[index] = Symbol('%s_%s' % (prefix, ''.join(map(str, index))), **kwargs) return arr A = Matrix(mySyms('a',(4,4),real=True)) A.col_del(0) A.row_del(0) print('A矩阵:') pprint(A) def mat_diff(M:Matrix): from numpy import ndindex M_det = M.det() for index in ndindex(M.shape): M[index] = diff(M_det,M[index]) return M print('标量对矩阵的求导:') pprint(mat_diff(A)) print('A的伴随矩阵:') pprint(A.T)
向量及矩阵对标量求导

标量对向量及矩阵求导
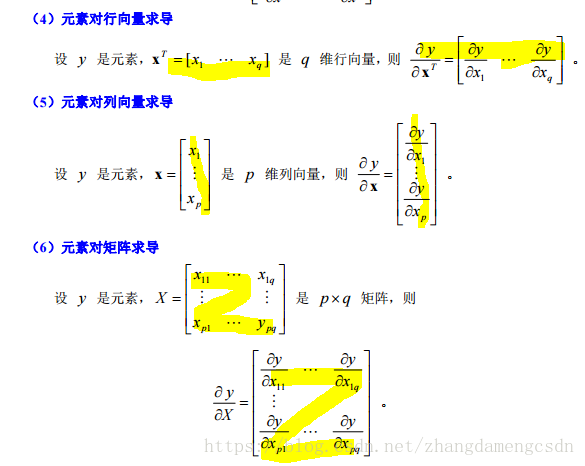
行向量对列向量与列向量对行向量

行向量对行向量与列向量对列向量
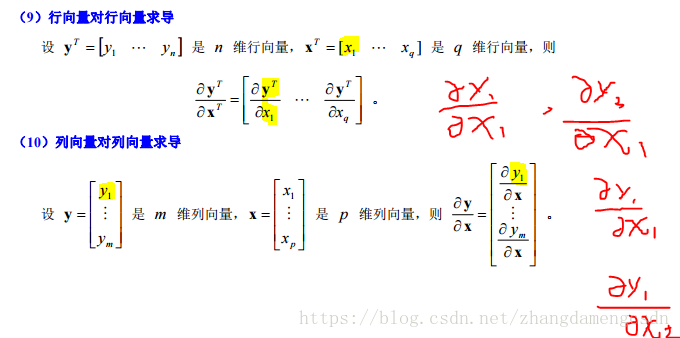
矩阵对行向量以及列向量

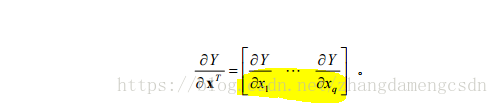
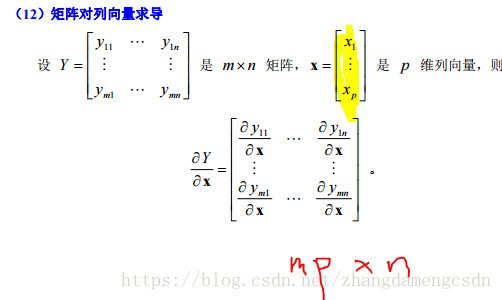
对矩阵求导




 浙公网安备 33010602011771号
浙公网安备 33010602011771号