AVL树学习笔记
AVL树
注意!!!
本文学习参考自AVL树(一)之 图文解析 和 C语言的实现,这篇博客写的非常棒!讲解易懂,思路清晰,代码也写的非常好!大家快去看看!!(这里的代码就是参考(抄)他的,我懒= =)
为什么要有AVL树?
AVL树是最先被发明的高度自平衡二叉查找树。AVL树的名字取自它的发明者G.M.Adeison-Velsky和E.M.Landis的首字母。
所以平衡和不平衡有什么区别。我们先来看看原始的二叉搜索树。

这两棵都是二叉搜索树,他们可以很方便的进行结点的二分搜索。如果这个二叉树是比较工整(平衡)的话,那搜索的复杂度将会是O(lgn)。但根据我们创建二叉搜索树时插入结点顺序的不同,比如说,我们以6,5,4,3,2,1的顺序插入结点创建的话,会有:
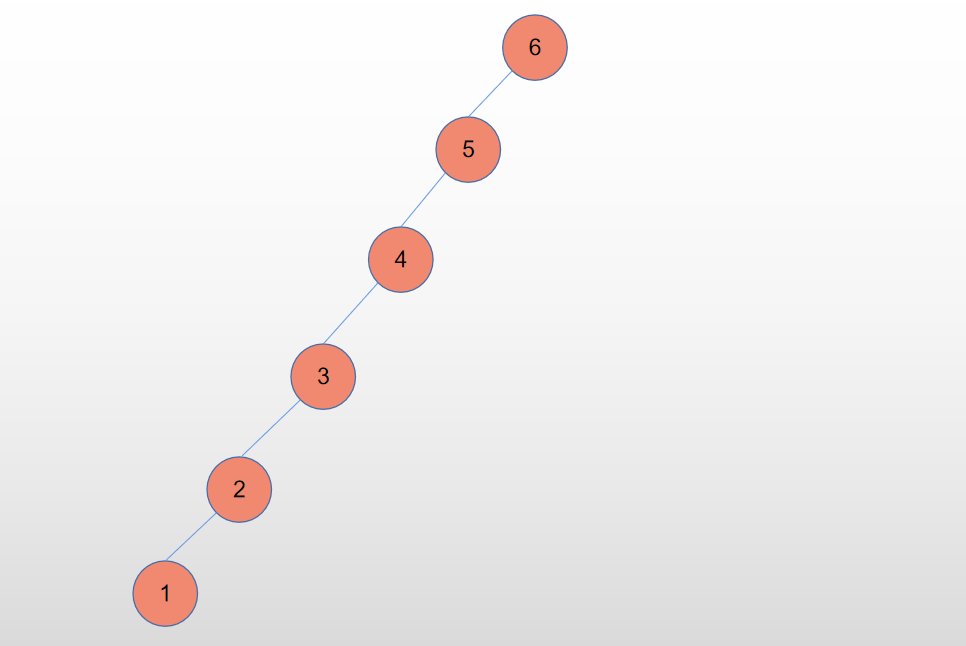
这课树已经退化成了线性表了,对它进行查找的性能将大大折扣。究其原因,是因为这颗二叉搜索树的结点都偏向一边了,导致左右不平衡!所以我们要让他平衡。
AVL树的特点
- 本身首先是一棵二叉搜索树。
- 带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)小于2,且取值只能是-1,0或1。
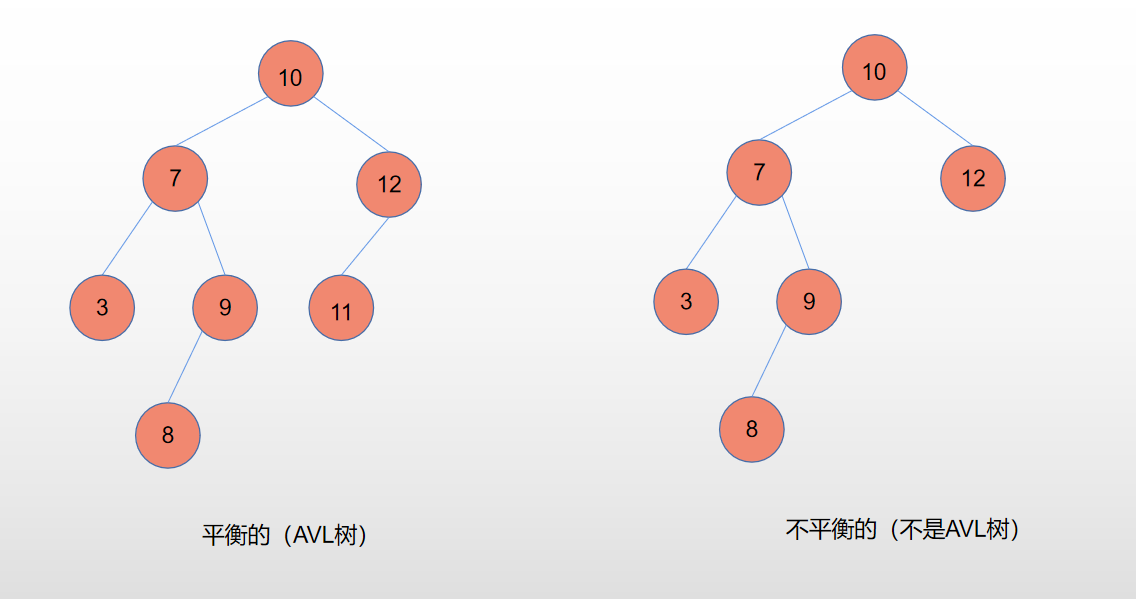
AVL树的增删查的时间复杂度都是O(lgn)。
AVL树结构的定义
typedef struct node {
int key;
int height; //用来计算平衡因子
node* left;
node* right;
}Node, *AVLTree;
AVL树旋转
AVL树插入或者删除节点后可能会导致其不再平衡,而需要调整。根据插入的位置不同,有LL、RR、LR、RL四种情况。
1.LL型:
LL的意思是,在(L)子树的(L)左孩子上插入结点,导致树不平衡。它需要进行一次右旋来恢复平衡。
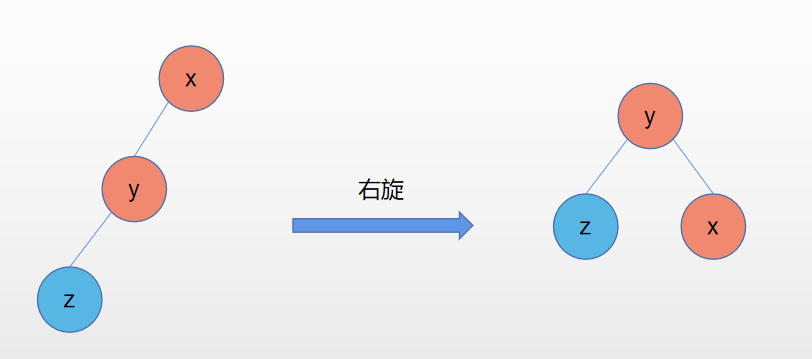
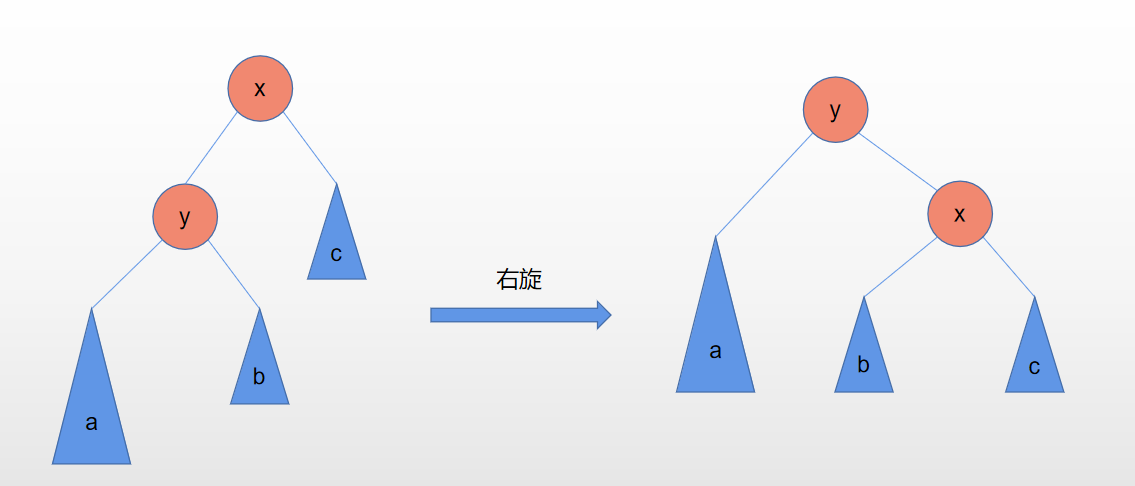
//LL右单旋
Node* LL_rotation(AVLTree x) {
AVLTree y;
//旋转
y = x->left;
x->left = y->right;
y->right = x;
//更新高度
x->height = max(HEIGHT(x->left), HEIGHT(x->right)) + 1;
y->height = max(HEIGHT(y->left), x->height) + 1;
return y;
}
2.RR型:
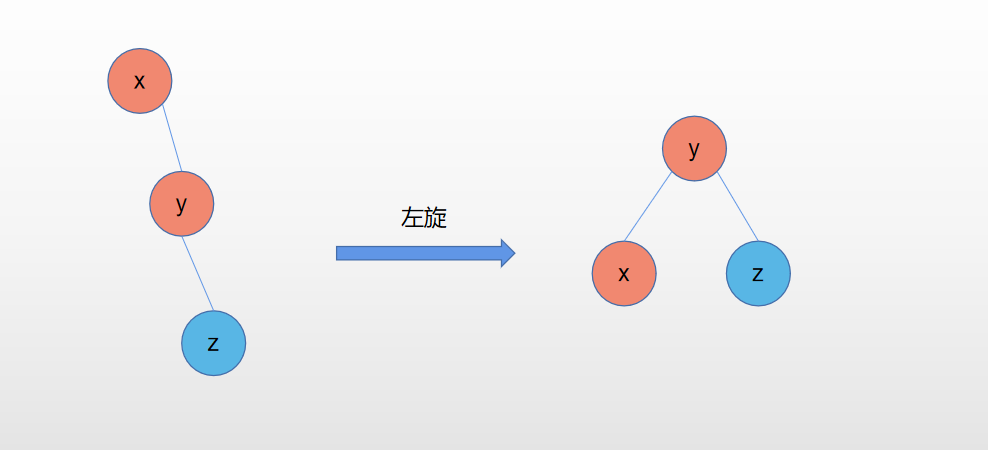
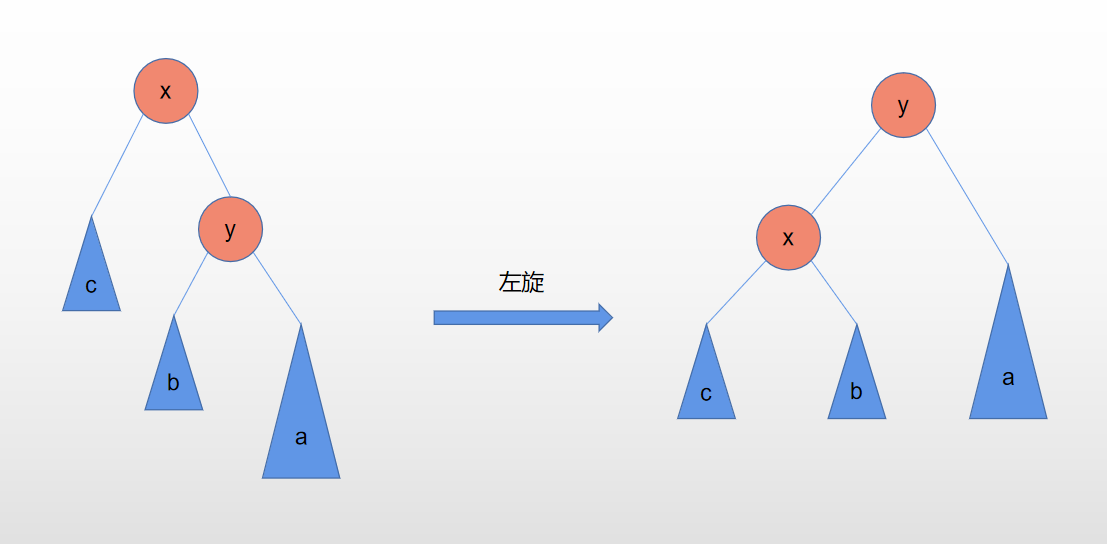
//RR左单旋
Node* RR_rotation(AVLTree x) {
AVLTree y;
//旋转
y = x->right;
x->right = y->left;
y->left = x;
//更新高度
x->height = max(HEIGHT(x->left), HEIGHT(x->right)) + 1;
y->height = max(HEIGHT(y->right), x->height) + 1;
return y;
}
3.LR型:
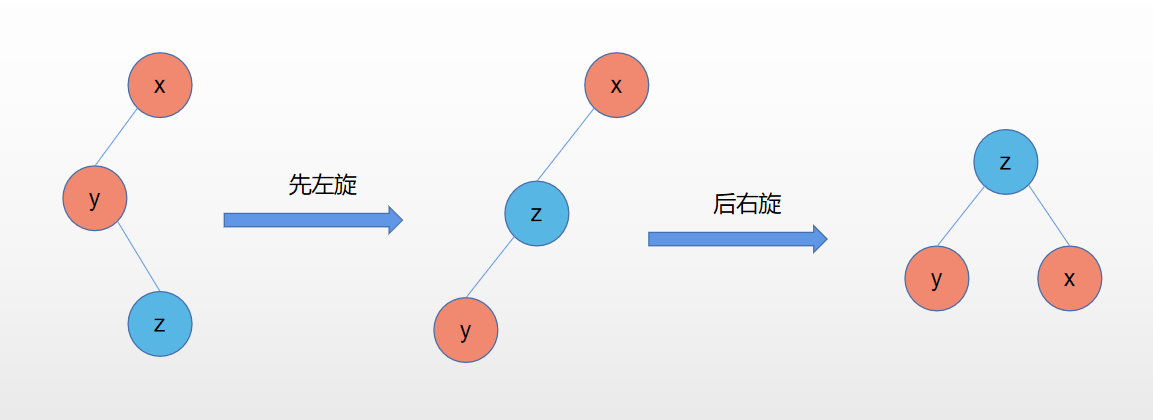
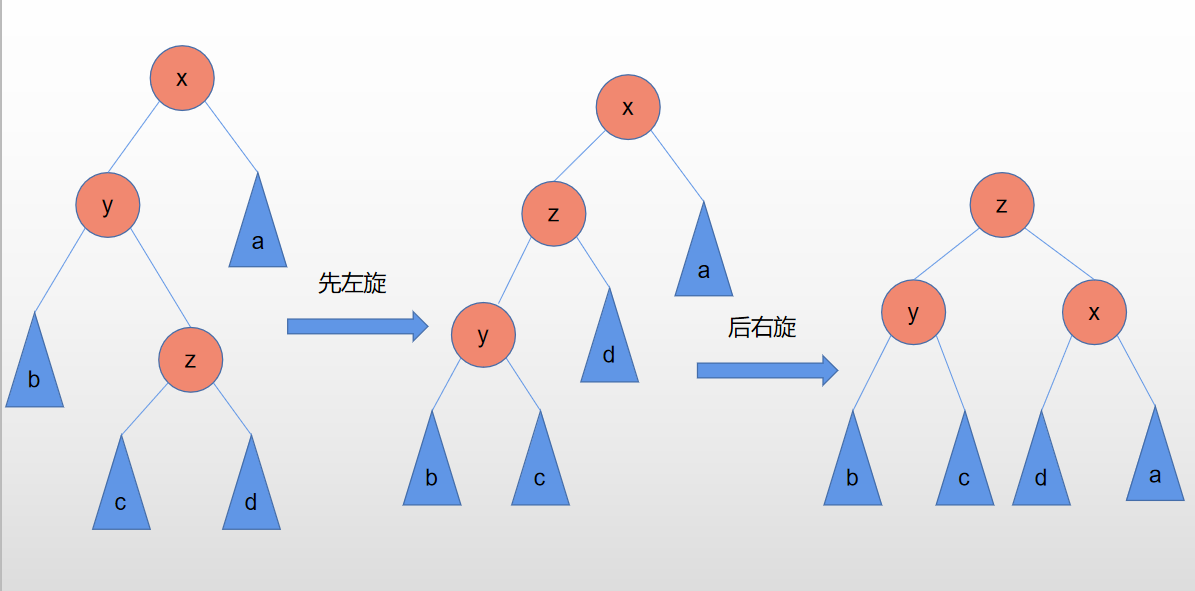
//LR左右双旋
Node* LR_rotation(AVLTree x) {
x->left = RR_rotation(x->left);
return LL_rotation(x);
}
4.RL型:
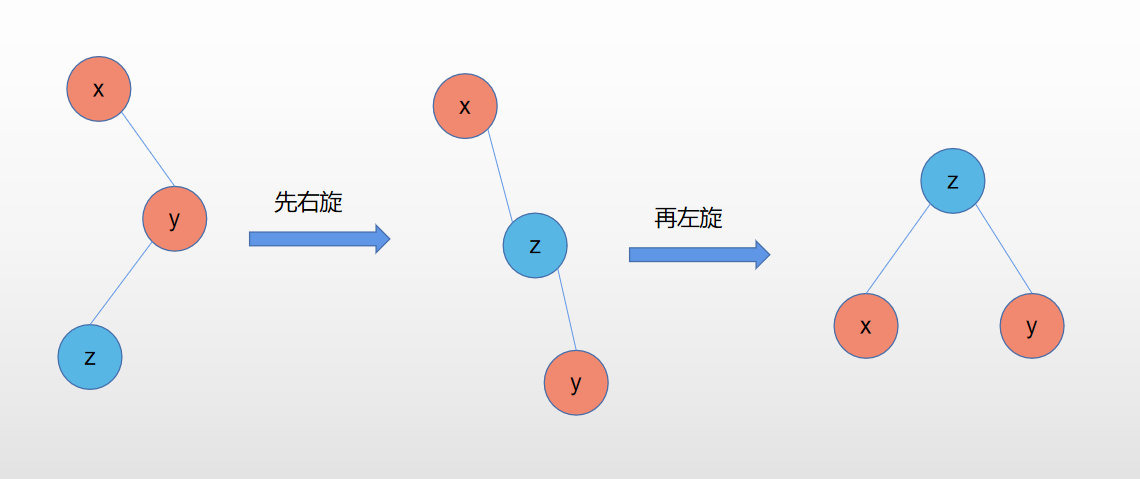

//RL右左双旋转
Node* RL_rotation(AVLTree x) {
x->right = RR_rotation(x->right);
return LL_rotation(x);
}
AVL树插入结点
AVL树插入结点时可能会引起不平衡,这种不平衡可能并不体现在被插入的那个最小的子树中,而是在它的上层,所以需要用递归的方法从下往上进行调整,或者改写数据结构,给结点增加一个指向父节点的指针,在迭代时向上回游。
//插入(递归进行插入和调整)
//调整的过程也是递归的,因为在子树中插入结点导致的不平衡可能会在上层或者向上传播
Node* insert_node(AVLTree tree, int key) {
//终止条件,到末尾了,就创建该待插入结点
if (tree == NULL) {
tree = avltree_create_node(key, NULL, NULL);
}
//在左子树插入
else if (key <= tree->key) {
tree->left = insert_node(tree->left, key);
//插入结点后如果失去平衡,就要进行相应的调节
if (HEIGHT(tree->left) - HEIGHT(tree->right) == 2) {
//LL型
if (key < tree->left->key) {
tree = LL_rotation(tree);
}
//LR型
else {
tree = LR_rotation(tree);
}
}
}
//在右子树插入
else{
tree->right = insert_node(tree->right, key);
//失衡调整
if (HEIGHT(tree->right) - HEIGHT(tree->left) == 2) {
//RR型
if (key > tree->right->key) {
tree = RR_rotation(tree);
}
else {
tree = RL_rotation(tree);
}
}
}
//重新计算高度
tree->height = max(HEIGHT(tree->left), HEIGHT(tree->right)) + 1;
return tree;
}
AVL树删除结点
删除结点和添加结点类似。
//递归进行删除和调整
Node* delete_node(AVLTree tree, int key) {
//如果找不到,就返回空
if (tree == NULL) {
return NULL;
}
//在左子树中
if (key < tree->key) {
tree->left = delete_node(tree->left, key);
//失衡调整
if (HEIGHT(tree->right) - HEIGHT(tree->left) == 2) {
Node* r = tree->right;
if (HEIGHT(r->left) > HEIGHT(r->right))
tree = RL_rotation(tree);
else
tree = RR_rotation(tree);
}
}
//在右子树中
else if (key > tree->key) {
tree->right = delete_node(tree->right, key);
//失衡调整
if (HEIGHT(tree->left) - HEIGHT(tree->right) == 2) {
Node* l = tree->left;
if (HEIGHT(l->left) > HEIGHT(l->right))
tree = LL_rotation(tree);
else
tree = LR_rotation(tree);
}
}
//找到要删除结点
else {
//左右子树非空
if (tree->left&&tree->right) {
//左子树比右子树高,用前驱节点顶替
if (HEIGHT(tree->left) > HEIGHT(tree->right)) {
Node* pre = maximum(tree->left);
tree->key = pre->key;
//在左子树递归删除替身结点
tree->left = delete_node(tree->left, pre->key);
}
//右子树比左子树高,用后继结点顶替
else {
Node* suc = minmum(tree->right);
tree->key = suc->key;
//在右子树递归删除替身结点
tree->right = delete_node(tree->right, suc->key);
}
}
//其中一个子树为空
else {
//记住待删除结点
Node* tmp = tree;
tree = tree->left ? tree->left : tree->right;
delete tree;
}
}
//重新计算高度
if(tree)
tree->height = max(HEIGHT(tree->left), HEIGHT(tree->right)) + 1;
return tree;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号