7-10周总结

前言：本阶段考查继承与多态、抽象类的使用，同时也考查了学生是否巩固对类的使用。题目量虽然不多，仅仅只有四五道题，但是难度与上一个阶段相比更加困难 。

1.题目集4 7-2 点线形系列4-凸四边形的计算

（1）设计与分析

 

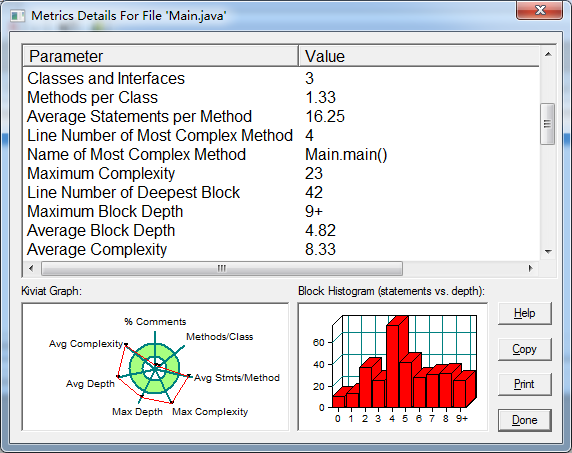
 本题我采用了点和直线这两个类，其中点类包含横坐标和纵坐标，直线类包含两个点横纵坐标的差、长度、直线的斜率。因为需要使用多个点和线，所以我采用了对象数组，避免繁琐地重复定义多个类。从图中可以看出，我对方法的使用比较少，而且主类中代码很复杂。有些情况相同的地方应使用方法，减少重复使用同样的语句，使代码更加简洁。对于三个点在同一直线上的问题，我使用了方法，只需判断三个点构成的三条直线任意的两条直线的斜率是否相等即可。

（2）采坑心得

dx = point[i].x - point[i - 2].x;
dy = point[i].y - point[i - 2].y;
a = (dx * line[i - 3].dx + dy * line[i - 3].dy);
b = -(dx * line[i - 2].dx + dy * line[i - 2].dy);
l1 = Math.sqrt(dx * dx + dy * dy);
p = (line[i - 1].leng + line[i - 2].leng + l1) / 2;
squa = Math.sqrt(p * (p - line[i - 1].leng) * (p - line[i - 2].leng) * (p - l1));
p = (line[i].leng + line[i - 3].leng + l1) / 2;
squb = Math.sqrt(p * (p - line[i - 3].leng) * (p - line[i].leng) * (p - l1));
s = squa + squb;
if(a < 0 && b < 0){
System.out.println("false " + (int)(c * 1000 + 0.5) / 1000.0 + " " + (int)(s * 1000 + 0.5) / 1000.0);
return;
}

对于四边形凹凸的判断，我采用了向量的方法。当四边形其中一个点与其对角上的点形成一个向量，与相邻的两个点分别形成两个向量，这两个向量分别与前者相乘，会得到两个结果，如果这两个结果都为负数，那么这个四边形是凹四边形，反之则为凸四边形。

（3）改进建议

每个选项后面都有正则表达式的判断，可以在选项前判断，然后在选项后判断点的数量，避免代码多余。

2.7-1 点与线（类设计）

（1）设计与分析

 

 

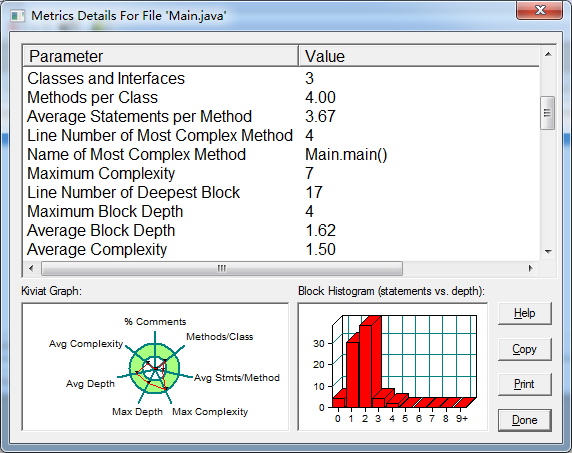
 本题较为简单，只需设计点和直线类及其相关属性即可。由图可以得知，代码并不复杂，类的设计合理。

（2）采坑心得

System.out.print(String.format("%.2f",this.x) + "," + String.format("%.2f",this.y));

如果用(int)(this.x*100+0.5)/100.0的话，会使代码较长，而String类的format方法可以简便地将数据后面的小数位数保留。

（3）改进建议

代码比较简单，因此无需改进代码。

3.7-2 点线面问题重构（继承与多态）

（1）设计与分析

 

 

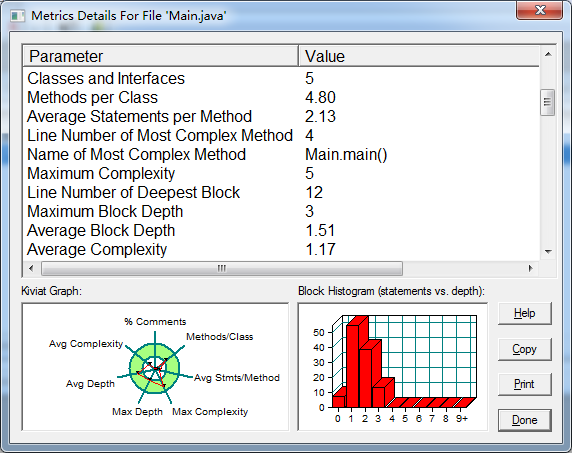
 在Point类和Line类基础上添加Element的父类，该父类为抽象类，并且添加Element的子类Plane。Point类、Line类和Plane类都继承自Element类。

（2）采坑心得

在抽象类Element中需要将public void display() {}改为抽象方法abstract public void display();否则不符合题意；注意如何使用多态，使父类变量引用子类对象及相对应的方法。

4.7-3 点线面问题再重构（容器类）

 （1）设计与分析

 

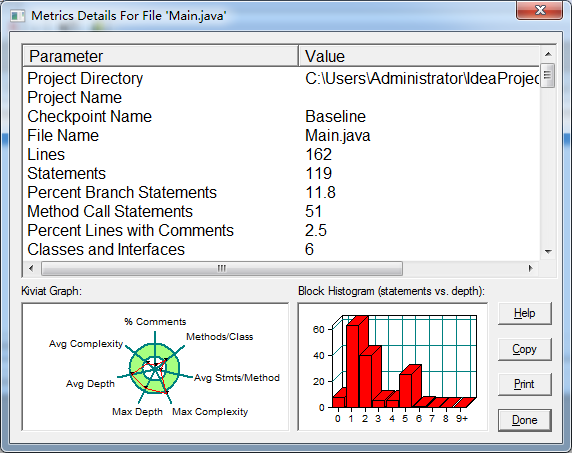
 在7-2 点线面问题重构（继承与多态）继承上添加容器类GeometryObject，其属性为ArrayList<Element>类型的对象；使其可以通过选项来进行相应的使用，用容器来存储当前所以数据。

（2）采坑心得

首先要掌握ArrayList<Element>类型的对象如何使用，理解之间的关系，梳理逻辑关系，防止写到后面有些懵；删除容器中第index - 1个数据时需要进行判断，要删除的数据不能小于0或大于容器的大小。

 

总结

在第二阶段的学习中，我学到了如何将一个类继承另一个类、使用多态、容器和抽象类。但是我仍然不够深入学习这些知识点，这说明了我在本阶段的学习不太能应用学过的内容来解决题目中的问题。我还需多加练习才能巩固我学过的内容。