浅谈斜率优化
如果一个 DP 的转移方程可以写成 \(f_i=\underset{j<i}{\min\!/\!\max}\>\{f_j+a_i\times b_j+c_i+d_j\}+C\) 的形式，那么可以运用斜率优化。
不妨设转移是 \(\min\)，忽略那个常数 \(C\)，设 \(g_{i,j}=f_j+a_i\times b_j+c_i+d_j\)，即 \(f_i=\min\limits_{j<i}g_{i,j}\)，式子可以化为 \(f_j+d_j=-a_i\times b_j+g_{i,j}-c_i\)，设 \(y_j=f_j+d_j\)，\(k=-a_i\)，\(x_j=b_j\)，\(t_j=g_{i,j}-c_i\)，原式化为 \(y_j=kx_j+t_j\>\,(*)\)，这是一个一次函数的形式。
假设 \(f_i\) 是由 \(p\) 转移来的，即 \(f_i=g_{i,p}=\min_{j<i}g_{i,j}\)，因为 \(t_j=g_{i,j}-c_i\)，所以 \(t_p=\min_{j<i}t_j\)。 注意到 \((*)\) 式中 \(k\) 是一个定值，这说明，如果过每个点 \((x_j,y_j)\) 画斜率为 \(k\) 的直线 \(l_j\)，则 \(l_p\) 在 \(y\) 轴的截距是最小的，直观地说就是“在最下面”的。
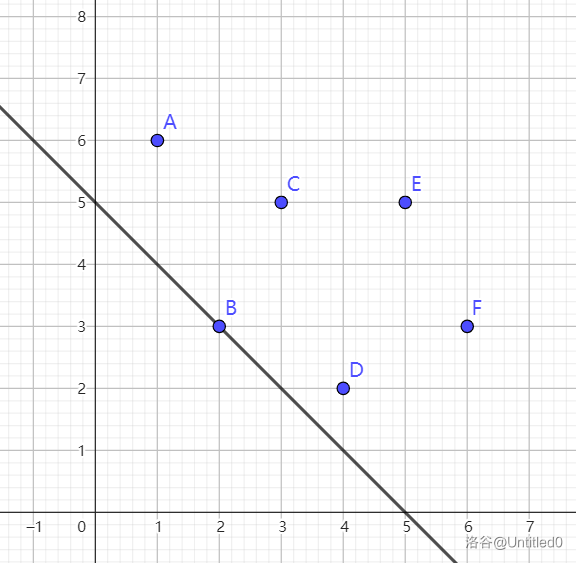
（如图，假设有这些点，我们要画一条斜率为 \(-1\) 的直线（\(k=-1\)），则图中那条是最优的，其 \(y\) 轴截距是 \(5\)，最小）
现在考虑如何快速找到这条最优直线：维护这些点的下凸壳，则与这个凸壳相切的直线是最优的。
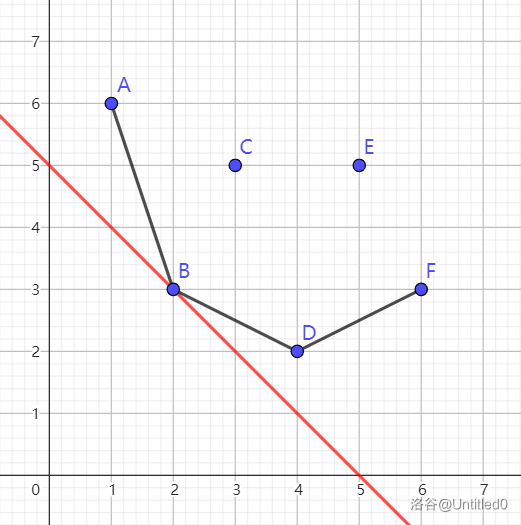
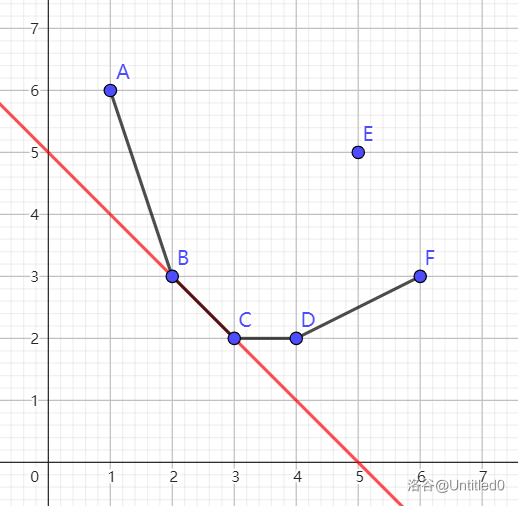
（如图，两种相切）
下凸壳的斜率单调递增，切点就是满足切线斜率 \(\ge\) 左边的斜率 且 \(<\) 右边的斜率的点。
维护这个东西需要动态凸包，但是多数情况下并不需要：
- 如果 \(x\) 单调，\(k\) 也单调，则决策点 \(p\) 只会单向移动，单调队列维护即可。推荐构造 \(x\) 递增，因为这样可能比较直观。
- 如果 \(x\) 单调，用单调栈维护凸壳，然后二分即可。
- 否则才需要动态凸包 / 李超线段树。
事实上推式子的时候一般不需要把常数项写出来，只要搞清楚 \(x,y,k\) 就可以了。
注意特判斜率不存在的情况。
例题
\[\begin{aligned}
f_i&=\min_{j<i}\{f_j+c_i+\sum_{k=j+1}^ip_k\times(x_i-x_k)\}\\
&=\min_{j<i}\{f_j+c_i+\sum_{k=j+1}^ip_k\times x_i-p_k\times x_k\}
\end{aligned}
\]
求出 \(p_i\) 的前缀和 \(t\) 和 \(p_i\times x_i\) 的前缀和 \(s\)，原式化为：
\[\begin{aligned}
&f_i=\min_{j<i}\{f_j+c_i+x_i\times(t_i-t_j)-(s_i-s_j)\}\\
&g_{i,j}+s_j=x_i\times t_j+f_i-c_i-x_i\times t_i
\end{aligned}
\]
\(x=t,k=x\) 均单调递增，所以决策点只会后移，单调队列维护凸壳，时间复杂度 \(O(n)\)。
注意不要用 double 算斜率，容易因为精度 WA，要用 long double 或者把斜率不等式化成乘法形式。
本题 \(p\) 可能 \(=0\)，所以不一定在最后一个地方建仓库，并且斜率可能不存在。
#include<bits/stdc++.h>
#define endl '\n'
#define rep(i, s, e) for(int i = s, i##E = e; i <= i##E; ++i)
#define per(i, s, e) for(int i = s, i##E = e; i >= i##E; --i)
#define F first
#define S second
#define int ll
#define gmin(x, y) (x = min(x, y))
#define gmax(x, y) (x = max(x, y))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double f128;
typedef pair<int, int> pii;
constexpr int N = 1e6 + 5;
int n, x[N], p[N], c[N], t[N], s[N], f[N];
int q[N], l = 1, r;
inline int Y(int i) { return f[i] + s[i]; }
inline int X(int i) { return t[i]; }
inline int K(int i) { return x[i]; }
signed main() {
#ifdef ONLINE_JUDGE
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
#endif
cin >> n;
rep(i, 1, n) {
cin >> x[i] >> p[i] >> c[i];
t[i] = t[i - 1] + p[i];
s[i] = s[i - 1] + p[i] * x[i];
}
q[++r] = 0;
rep(i, 1, n) {
while(l < r && Y(q[l + 1]) - Y(q[l]) <= K(i) * (X(q[l + 1]) - X(q[l])))
++l;
int p = q[l];
f[i] = f[p] + c[i] + x[i] * (t[i] - t[p]) - (s[i] - s[p]);
while(l < r)
if(X(q[r]) - X(q[r - 1]) == 0) {
if(Y(q[r]) - Y(q[r - 1]) > 0) --r;
else break;
}
else if(X(i) - X(q[r]) == 0) {
if(Y(i) - Y(q[r]) < 0) --r;
else break;
}
else if((Y(q[r]) - Y(q[r - 1])) * (X(i) - X(q[r])) >= (Y(i) - Y(q[r])) * (X(q[r]) - X(q[r - 1])))
--r;
else break;
q[++r] = i;
}
int tmp = n;
while(!p[tmp]) --tmp;
cout << *max_element(f + tmp, f + n + 1) << endl;
return 0;
}
其实我觉得这个 \(n^2\) DP 挺难想到的。。。
\[\begin{aligned}
&f_i=\min_{j<i}\{f_j+t_i\times(c_i-c_j)+s\times(c_n-c_j)\}\\
&g_{i,j}-s\times c_j=t_i\times c_j+f_i-t_i\times c_i-s\times c_n
\end{aligned}
\]
其中 \(t\) 和 \(c\) 是原题中 \(T\) 和 \(C\) 的前缀和。提前计算了启动机器的代价。
本题中 \(x=c\) 单增，但 \(k=t\) 不单调，所以需要单调栈 + 二分，时间复杂度 \(O(n\log n)\)。
注意不等式变号问题。
#include<bits/stdc++.h>
#define endl '\n'
#define rep(i, s, e) for(int i = s, i##E = e; i <= i##E; ++i)
#define per(i, s, e) for(int i = s, i##E = e; i >= i##E; --i)
#define F first
#define S second
#define int ll
#define gmin(x, y) (x = min(x, y))
#define gmax(x, y) (x = max(x, y))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double f128;
typedef pair<int, int> pii;
constexpr int N = 3e5 + 5;
int n, s, c[N], t[N], f[N];
int stk[N], tp;
inline int Y(int i) { return f[i] - s * c[i]; }
inline int X(int i) { return c[i]; }
inline int K(int i) { return t[i]; }
// 下凸，斜率单增
inline int find(int k) {
int l = 1, r = tp;
while(l < r) {
int mid = (l + r) / 2;
if(Y(stk[mid]) - Y(stk[mid + 1]) <= k * (X(stk[mid]) - X(stk[mid + 1])))
// X 的差是负的，挪过来要变号（这里是我的写法问题）
r = mid;
else l = mid + 1;
}
return stk[l];
}
signed main() {
#ifdef ONLINE_JUDGE
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
#endif
cin >> n >> s;
rep(i, 1, n) {
cin >> t[i] >> c[i];
t[i] += t[i - 1], c[i] += c[i - 1];
}
stk[++tp] = 0;
rep(i, 1, n) {
int p = find(K(i));
f[i] = f[p] + t[i] * (c[i] - c[p]) + s * (c[n] - c[p]);
while(tp > 1 && (Y(stk[tp]) - Y(stk[tp - 1])) * (X(i) - X(stk[tp])) >=
(Y(i) - Y(stk[tp])) * (X(stk[tp]) - X(stk[tp - 1])))
--tp;
stk[++tp] = i;
}
cout << f[n] << endl;
return 0;
}
注意到当 \(w_i<w_j\land l_i<l_j\) 时 \(i\) 和 \(j\) 放一组一定不劣，所以从小到大排序后保留有用的值，然后容易得出 DP：
\[\begin{aligned}
&f_i=\min_{j<i}f_j+w_i\times l_{j+1}\\
&g_{i,j}=w_i\times(-l_{j+1})+f_i
\end{aligned}
\]
单调队列维护即可，时间复杂度 \(O(n\log n)\)，瓶颈在排序。
被这题调破防了。别去分母了，安心用 long double 吧，128 位的精度还是够的。以及新旧数组不要弄混。
#include<bits/stdc++.h>
#define endl '\n'
#define rep(i, s, e) for(int i = s, i##E = e; i <= i##E; ++i)
#define per(i, s, e) for(int i = s, i##E = e; i >= i##E; --i)
#define F first
#define S second
#define int ll
#define gmin(x, y) (x = min(x, y))
#define gmax(x, y) (x = max(x, y))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double f128;
typedef pair<int, int> pii;
constexpr int N = 5e4 + 5;
int n, m, f[N], q[N], l = 1, r;
pii a[N], b[N];
inline f128 slp(int i, int j) {
return f128(f[i] - f[j]) / f128(b[j + 1].S - b[i + 1].S);
}
signed main() {
#ifdef ONLINE_JUDGE
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
#endif
cin >> n;
rep(i, 1, n) cin >> a[i].F >> a[i].S;
sort(a + 1, a + n + 1);
rep(i, 1, n) {
while(m && a[i].S >= b[m].S) --m;
b[++m] = a[i];
}
q[++r] = 0;
rep(i, 1, m) {
while(l < r && slp(q[l], q[l + 1]) <= b[i].F) ++l;
int p = q[l];
f[i] = f[p] + b[i].F * b[p + 1].S;
while(l < r && slp(q[r], q[r - 1]) >= slp(i, q[r])) --r;
q[++r] = i;
}
cout << f[m] << endl;
return 0;
}
求出 \(x\) 的前缀和数组 \(s\)，容易得到 DP：
\[\begin{aligned}
f_i&=\max_{j<i}\{f_j+a(s_i-s_j)^2+b(s_i-s_j)+c\}\\
&=\max_{j<i}\{f_j-2as_is_j+as_i^2+bs_i+as_j^2-bs_j+c\}\\
\end{aligned}
\]
\[g_{i,j}+as_j^2-bs_j=2as_is_j+f_i-as_i^2-bs_i-c
\]
二次函数展开还是斜率优化的形式，单调队列维护，时间复杂度 \(O(n)\)。
#include<bits/stdc++.h>
#define endl '\n'
#define rep(i, s, e) for(int i = s, i##E = e; i <= i##E; ++i)
#define per(i, s, e) for(int i = s, i##E = e; i >= i##E; --i)
#define F first
#define S second
#define int ll
#define gmin(x, y) (x = min(x, y))
#define gmax(x, y) (x = max(x, y))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double f128;
typedef pair<int, int> pii;
constexpr int N = 1e6 + 5;
int n, a, b, c, s[N], f[N], q[N], l = 1, r;
inline int Y(int i) { return f[i] + a * s[i] * s[i] - b * s[i]; }
inline int X(int i) { return s[i]; }
inline int K(int i) { return 2 * a * s[i]; }
inline f128 slp(int i, int j) {
return f128(Y(i) - Y(j)) / f128(X(i) - X(j));
}
signed main() {
#ifdef ONLINE_JUDGE
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
#endif
cin >> n >> a >> b >> c;
rep(i, 1, n) cin >> s[i], s[i] += s[i - 1];
q[++r] = 0;
rep(i, 1, n) {
while(l < r && slp(q[l], q[l + 1]) >= K(i)) ++l;
int p = q[l];
f[i] = f[p] + a * (s[i] - s[p]) * (s[i] - s[p]) + b * (s[i] - s[p]) + c;
while(l < r && slp(q[r], q[r - 1]) <= slp(i, q[r])) --r;
q[++r] = i;
}
cout << f[n] << endl;
return 0;
}
求出 \(C\) 的前缀和数组 \(s\)，DP 式显然：
\[\begin{aligned}
f_i&=\min_{j<i}\{f_j+(i-j - 1+s_i-s_j-L)^2\}\\
&=\min_{j<i}\{f_j+[(i+s_i)-(j+s_j)-(L+1)]^2\}
\end{aligned}
\]
设 \(v_i=i+s_i\)，令 \(L\leftarrow L+1\)，则有：
\[\begin{aligned}
f_i&=\min_{j<i}\{f_j+(v_i-v_j-L)^2\}\\
&=\min_{j<i}\{f_j-2v_iv_j+v_i^2-2Lv_i+v_j^2+2Lv_j+L^2\}
\end{aligned}
\]
单调队列维护，时间复杂度 \(O(n)\)。
#include<bits/stdc++.h>
#define endl '\n'
#define rep(i, s, e) for(int i = s, i##E = e; i <= i##E; ++i)
#define per(i, s, e) for(int i = s, i##E = e; i >= i##E; --i)
#define F first
#define S second
#define int ll
#define gmin(x, y) (x = min(x, y))
#define gmax(x, y) (x = max(x, y))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double f128;
typedef pair<int, int> pii;
constexpr int N = 5e4 + 5;
int n, L, s[N], f[N], q[N], l = 1, r;
inline int V(int i) { return i + s[i]; }
inline int Y(int i) { return f[i] + V(i) * V(i) + 2 * L * V(i); }
inline int X(int i) { return V(i); }
inline int K(int i) { return 2 * V(i); }
inline f128 slp(int i, int j) {
return f128(Y(i) - Y(j)) / f128(X(i) - X(j));
}
signed main() {
#ifdef ONLINE_JUDGE
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
#endif
cin >> n >> L; ++L;
rep(i, 1, n) cin >> s[i], s[i] += s[i - 1];
q[++r] = 0;
rep(i, 1, n) {
while(l < r && slp(q[l], q[l + 1]) <= K(i)) ++l;
int p = q[l];
f[i] = f[p] + (V(i) - V(p) - L) * (V(i) - V(p) - L);
while(l < r && slp(q[r], q[r - 1]) >= slp(i, q[r])) --r;
q[++r] = i;
}
cout << f[n] << endl;
return 0;
}
浙公网安备 33010602011771号