算法学习第一天-汉诺塔问题

今天面试被打击坏了、准备重新拾起博客，记录学习，先啃算法，其实大学时候挺喜欢数学的、哎，这么多年也不知道梦想哪里去了。

首先看问题：

相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如图1)。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

-------------摘自百度百科

 

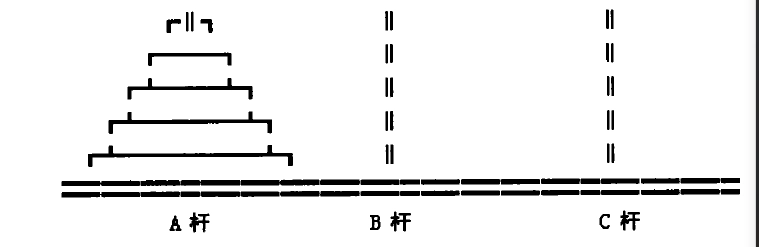
说白了，就是在只有三根杆子的情况下，将N个盘子，从A移动到C

这时候我们首先先看两个盘子的情况。

两个盘子只需要A=>B  A=>C  B=>C 三步就可以了。

也就是

第一步：将第一个盘子从A移动到B

第二步：将第二个盘子从A移动到C

第三步：将第一个盘子从B移动到C

当我们有N个盘子的时候，就可以把这个问题，看成第N个盘子，和(1+2+3+4+....+N-1)个盘子两部分来进行

但是如果是超过两个盘子的时候，想进行第一步，则势必会通过C来进行中转。

所以这三步也就变成了：

第一步：将(1+2+3+4+....+N-1)个盘子，从A经过C移动到B

第二步：将第N个盘子，从A移动到C

第三步：将(1+2+3+4+....+N-1)个盘子，从B经过A移动到C

至于这N-1个盘子怎么移动、就可以继续参考这三步，进行递归。

//这里N代表盘子数，A是开始点，B是经过点，C是目的地
const hanoi = function(n,a,b,c){
                     if(n>0){
                                hanoi(n-1,a,c,b)
                                console.log(`第${n}个盘子从${a}移动${c}`)
                                hanoi(n-1,b,a,c)
                    }
                 }

看到代码是不是很简单，其实没必要去理解递归的进行、程序会自动的运行下去，直到只剩两个盘子的时候，然后执行移动

主要是理解算法的思维模型。

 

千里之行始于足下，学习使我快乐