第九届蓝桥杯(省赛)C++C组真题题解
文章目录
剩余题目同B组真题相同,已给出B组真题题目链接:博客链接
题目链接
C组真题(剩余题目同B组真题相同,已给出B组真题题目链接)
题目结构
| 题目 | 类型 | 分值 |
|---|---|---|
| 第一题 | 结果填空 | 5分 |
| 第二题 | 结果填空 | 9分 |
| 第三题 | 结果填空 | 13分 |
| 第四题 | 结果填空 | 17分 |
| 第五题 | 代码填空 | 7分 |
| 第六题 | 代码填空 | 11分 |
| 第七题 | 程序设计 | 19分 |
| 第八题 | 程序设计 | 21分 |
| 第九题 | 程序设计 | 23分 |
| 第十题 | 程序设计 | 25分 |
第一题 哪天返回
-
问题重现
小明被不明势力劫持。后莫名其妙被扔到x星站再无问津。
小明得知每天都有飞船飞往地球,但需要108元的船票,而他却身无分文。
他决定在x星战打工。好心的老板答应包食宿,第1天给他1元钱。
并且,以后的每一天都比前一天多2元钱,直到他有足够的钱买票。
请计算一下,小明在第几天就能凑够108元,返回地球。输出
输出一个整数表示答案
-
解题思路
就是一个等差数列,利用公式求解可得。
-
代码
/**
*@filename:哪天返回
*@author: pursuit
*@CSDNBlog:unique_pursuit
*@email: 2825841950@qq.com
*@created: 2021-04-09 13:57
**/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 100000 + 5;
const int mod = 1e9+7;
void solve(){
}
int main(){
//等差数列求和公式得解。公差为2.
int n=1;
while(n*1+n*(n-1)*2/2<108){
n++;
}
cout<<n<<endl;//11
solve();
return 0;
}
-
答案
11 11 11
第二题 猴子分香蕉
-
问题重现
5只猴子是好朋友,在海边的椰子树上睡着了。这期间,有商船把一大堆香蕉忘记在沙滩上离去。
第1只猴子醒来,把香蕉均分成5堆,还剩下1个,就吃掉并把自己的一份藏起来继续睡觉。
第2只猴子醒来,重新把香蕉均分成5堆,还剩下2个,就吃掉并把自己的一份藏起来继续睡觉。
第3只猴子醒来,重新把香蕉均分成5堆,还剩下3个,就吃掉并把自己的一份藏起来继续睡觉。
第4只猴子醒来,重新把香蕉均分成5堆,还剩下4个,就吃掉并把自己的一份藏起来继续睡觉。
第5只猴子醒来,重新把香蕉均分成5堆,哈哈,正好不剩!
请计算一开始最少有多少个香蕉。输入
无
输出
输出一个整数表示答案
-
解题思路
一定要注意均分这个点,说明是可以整除的,我们只要枚举判断即可。
-
代码
/**
*@filename:猴子分香蕉
*@author: pursuit
*@CSDNBlog:unique_pursuit
*@email: 2825841950@qq.com
*@created: 2021-04-09 14:02
**/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 100000 + 5;
const int mod = 1e9+7;
//一定要注意均分这个点。假设一开始有香蕉x。
//说明(x-1) mod 5 我们设(x-1)*4/5=y
//说明(y-2)mod 5,我们设(y-2)*4/5=z
//则(z-3) mod 5,我们设(z-3)*4/5=u
//则(u-4) mod 5,我们设(u-4)*4/5=v
//则v mod 5;我们枚举x判断。
void solve(){
}
int main(){
int x,y,z,u,v;//3141
for(x=6;;x+=5){
y=(x-1)*4/5;
if((y-2)>0&&(y-2)%5==0){
z=(y-2)*4/5;
if((z-3)>0&&(z-3)%5==0){
u=(z-3)*4/5;
if((u-4)>0&&(u-4)%5==0){
v=(u-4)*4/5;
if(v>0&&v%5==0){
cout<<x<<endl;
break;
}
}
}
}
}
solve();
return 0;
}
-
答案
3141 3141 3141
第五题 书号验证
-
问题重现
2004年起,国际ISBN中心出版了《13位国际标准书号指南》。
原有10位书号前加978作为商品分类标识;校验规则也改变。
校验位的加权算法与10位ISBN的算法不同,具体算法是:
1、 用1分别乘ISBN的前12位中的奇数位(从左边开始数起),用3乘以偶数位,乘积之和以10为模,
2、10与模值的差值再对10取模(即取个位的数字)即可得到校验位的值,其值范围应该为0~9。
下面的程序实现了该算法,请仔细阅读源码,填写缺失的部分。
// 验证成功返回 1,否则返回 0 int f(const char* s) { int k=1; int sum = 0; int i; for(i=0; s[i]!='\0'; i++){ char c = s[i]; if(c=='-' || c==' ') continue; sum += _________________________________________ ; //填空 k++; if(k>12) break; } while(s[i]!='\0') i++; return (s[i-1]-'0') == (10-sum % 10)%10; } int main() { printf("%d\n",f("978-7-301-04815-3")); printf("%d\n",f("978-7-115-38821-6")); return 0; } -
解题思路
横线上所需填的即是我们需要判断是奇数位还是偶数位,由于只有一行,所以用
?:条件表达式语句即可。 -
答案
(c-'0')*(k%2?1:3)
第六题 稍小分数
-
问题重现
回到小学----
真分数:分子小于分母的分数
既约分数:分子分母互质,也就是说最大公约数是1
x星球数学城的入口验证方式是:
屏幕上显示一个真分数,需要你快速地找到一个比它小的既约分数,要求这个分数越大越好。
同时限定你的这个分数的分母不能超过100。如下代码很暴力地解决了这个问题,请仔细分析,并填写划线部分缺失的代码。
int gcd(int a, int b) { if(b==0) return a; return gcd(b, a%b); } int main() { // 这是屏幕上显示的那个分数 a/b int a = 7; int b = 13; int m,n; int max_a = 0; int max_b = 1; for(n=100; n>1; n--){ for(m=n-1; m>=1; m--){ if(m*b<a*n && gcd(m,n)==1){ if( __________________________________ ){ //填空 max_a = m; max_b = n; break; } } } } printf("%d/%d\n", max_a, max_b); return 0; } -
解题思路
由题意知此
if判断更新最大值,所以我们需要判断是否符合条件,由于都是整型数据且上一个if其实已经提示了,将分数之间的比较转化即 a / b > c / d ≡ a ∗ d > c / b a/b>c/d\equiv a*d>c/b a/b>c/d≡a∗d>c/b。 -
答案
m*max_b>n*max_a
第七题 次数差
-
问题重现
x星球有26只球队,分别用a~z的26个字母代表。他们总是不停地比赛。
在某一赛段,哪个球队获胜了,就记录下代表它的字母,这样就形成一个长长的串。
国王总是询问:获胜次数最多的和获胜次数最少的有多大差距?输入
输入存在多组数据,对于每组数据:
输入一行包含一个串,表示球队获胜情况(保证串的长度<1000)输出
对于每组数据:输出一个数字,表示出现次数最多的字母比出现次数最少的字母多了多少次。
样例输入
abaabcaa bbccccddaaaacccc样例输出
4 6 -
解题思路
利用map容器记录,最后遍历记录最大值和最小值即可得出答案。
-
代码
/**
*@filename:次数差
*@author: pursuit
*@CSDNBlog:unique_pursuit
*@email: 2825841950@qq.com
*@created: 2021-04-09 14:17
**/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 100000 + 5;
const int mod = 1e9+7;
map<char,int> p;
string s;
void solve(){
for(auto &x:s){
p[x]++;
}
int minn=1000,maxx=0;
for(auto &x:p){
minn=min(x.second,minn);
maxx=max(x.second,maxx);
}
cout<<maxx-minn<<endl;
}
int main(){
while(cin>>s){
p.clear();
solve();
}
return 0;
}
第八题 等腰三角形
-
问题重现
本题目要求你在控制台输出一个由数字组成的等腰三角形。
具体的步骤是:- 先用1,2,3,…的自然数拼一个足够长的串
- 用这个串填充三角形的三条边。从上方顶点开始,逆时针填充。比如,当三角形高度是8时 :
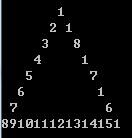
输入
输入存在多组数据,对于每组数据:
输入一行包含一个正整数n(3<n<300),表示三角形的高度输出
对于每组测试数据输出用数字填充的等腰三角形。
为了便于测评,我们要求空格一律用"."代替。样例输入
5 10样例输出
....1 ...2.1 ..3...2 .4.....1 567891011 .........1 ........2.2 .......3...2 ......4.....2 .....5.......1 ....6.........2 ...7...........0 ..8.............2 .9...............9 1011121314151617181 -
解题思路
首先我们要做的就是将这些整数连成一个串,然后根据坐标绘制即可。注意坐标的变化。
-
代码
/**
*@filename:等腰三角形
*@author: pursuit
*@CSDNBlog:unique_pursuit
*@email: 2825841950@qq.com
*@created: 2021-04-09 16:45
**/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 300 + 5;
const int mod = 1e9+7;
int n;
char graph[maxn][maxn];
string s;
void solve(){
for(int i=0;i<n;i++){
for(int j=0;j<n+i;j++){
graph[i][j]='.';
}
}
//开始填数。
int index=0;
//开始左边。
for(int i=0,j=n-1;i<n-1;i++,j--){
graph[i][j]=s[index++];
}
//开始底边。
for(int i=n-1,j=0;j<2*n-1;j++){
graph[i][j]=s[index++];
}
for(int i=n-2,j=2*n-3;i>0;i--,j--){
graph[i][j]=s[index++];
}
for(int i=0;i<n;i++){
for(int j=0;j<n+i;j++){
cout<<graph[i][j];
}
cout<<endl;
}
}
int main(){
s="";
for(int i=1;i<=200;i++){
s+=to_string(i);
}
while(cin>>n){
//cout<<s.size()<<endl;
solve();
}
return 0;
}
第九题 小朋友崇拜圈
-
问题重现
班里N个小朋友,每个人都有自己最崇拜的一个小朋友(也可以是自己)。
在一个游戏中,需要小朋友坐一个圈,
每个小朋友都有自己最崇拜的小朋友在他的右手边。
求满足条件的圈最大多少人?
小朋友编号为1,2,3,…N输入
输入第一行,一个整数N(3<N<100000)
接下来一行N个整数,由空格分开。表示每位小朋友崇拜的小朋友的编号。输出
输出一个整数,表示满足条件的最大圈的人数。
样例输入
9 3 4 2 5 3 8 4 6 9样例输出
4提示
如图所示,崇拜关系用箭头表示,红色表示不在圈中。
显然,最大圈是[2 4 5 3] 构成的圈
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LFYanJ1U-1618148068902)(第九届蓝桥杯(省赛)C++C组真题题解.assets/20191118000755_64238.png)] -
解题思路
我们可以用一个数组
friends来表示,其中friends[i]表示第 i i i个小朋友崇拜的人。那么,我们就可以用 d f s dfs dfs去搜索环的长度了,要注意的就是搜索完之后标记的清除。 -
代码
/**
*@filename:小朋友崇拜圈
*@author: pursuit
*@CSDNBlog:unique_pursuit
*@email: 2825841950@qq.com
*@created: 2021-04-09 17:26
**/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 100000 + 5;
const int mod = 1e9+7;
int n;//n个小朋友。
int friends[maxn];
int ans,maxx;
bool vis[maxn];
void dfs(int i,int obj){
if(vis[i]&&i!=obj){
return;
}
if(vis[i]&&i==obj){
//说明到达了。形成了一个回环。
maxx=max(ans,maxx);
return;
}
ans++;
vis[i]=true;
dfs(friends[i],obj);
vis[i]=false;
}
void solve(){
ans,maxx=0;
for(int i=1;i<=n;i++){
ans=0;
dfs(i,i);
}
cout<<maxx<<endl;
}
int main(){
while(cin>>n){
int temp;
for(int i=1;i<=n;i++){
cin>>temp;
friends[i]=temp;
}
solve();
}
return 0;
}
第十题 耐摔指数
-
问题重现
x星球的居民脾气不太好,但好在他们生气的时候唯一的异常举动是:摔手机。
各大厂商也就纷纷推出各种耐摔型手机。
x星球的质监局规定了手机必须经过耐摔测试,并且评定出一个耐摔指数来,之后才允许上市流通。
x星球有很多高耸入云的高塔,刚好可以用来做耐摔测试。
塔的每一层高度都是一样的,与地球上稍有不同的是,他们的第一层不是地面,而是相当于我们的2楼。
如果手机从第7层扔下去没摔坏,但第8层摔坏了,则手机耐摔指数=7。
特别地,如果手机从第1层扔下去就坏了,则耐摔指数=0。
如果到了塔的最高层第n层扔没摔坏,则耐摔指数=n
为了减少测试次数,从每个厂家抽样3部手机参加测试。
如果已知了测试塔的高度,并且采用最佳策略,在最坏的运气下最多需要测试多少次才能确定手机的耐摔指数呢?输入
输入存在多组测试数据,每组测试数据输入一个整数n(3<n<10000),表示测试塔的高度。
输出
对于每组测试数据,输出一个整数,表示最多测试多少次。
样例输入
3 7样例输出
2 3提示
- 手机a从2楼扔下去,坏了,就把b手机从1楼扔;否则a手机继续3层扔下
- a手机从4层扔,坏了,则下面有3层,b,c 两部手机2次足可以测出指数;
若是没坏,手机充足,上面5,6,7 三层2次也容易测出。
-
解题思路
我们试想,如果只有一个手机,那么直接暴力枚举就是答案了。可是现在有三个手机。二分?可以做吗?我们发现,对于二分法,如果每次枚举的点都碎了,那就无法得到答案了,显然不行,对于有无限个手机的时候这个才是最佳决策。那么这道题我们该怎么做呢?其实这道题蕴含着好多决策点,我们测一次楼层的时候即是一个状态,而且这状态显然是相互转移的,所以动态规划才是解决这道问题的关键。我们用 d p [ i ] [ j ] dp[i][j] dp[i][j]表示现在还有 i i i部手机且待测楼层有 j j j层时,最坏运气下的最少的测试次数。那么我们测试 k ( k ∈ [ 1 , j ] k(k\in [1,j] k(k∈[1,j]层时则有两种情况:
-
如果当前测的手机坏了,那么手机数量减一,并去下一层测试,此时待测楼层为 k − 1 k-1 k−1。
-
如果当前测的手机没坏,那么就去上一层测试,此时 j − k j-k j−k。
我们想要的状态为 d p [ 3 ] [ n ] dp[3][n] dp[3][n],我们已知的状态即是只有一个手机的时候,我们运气最差只能从 1 1 1测到 j j j,这样进行状态转移即可。
-
-
代码
/**
*@filename:耐摔指数
*@author: pursuit
*@CSDNBlog:unique_pursuit
*@email: 2825841950@qq.com
*@created: 2021-04-10 00:20
**/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 10000 + 5;
const int mod = 1e9+7;
int n;
int dp[4][maxn];//dp[i][j]表示有i部手机且待测j个楼层的运气最差的最少测试次数。
void solve(){
for(int i=1;i<=3;i++){
for(int j=1;j<=n;j++){
//不管有几部手机,最坏的次数就是从1到j测下去。
dp[i][j]=j;
}
}
//接下来开始模拟,
for(int i=2;i<=3;i++){
for(int j=1;j<=n;j++){
//模拟1~j的测试情况。
//如果坏了,则手机数量减1,并去下一层测试,否则没摔坏就去楼上测试。
for(int k=1;k<j;k++){
dp[i][j]=min(dp[i][j],max(dp[i-1][k-1],dp[i][j-k])+1);
}
}
}
cout<<dp[3][n]<<endl;
}
int main(){
while(cin>>n){
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号