Codeforces Round #633 (Div. 2) 题解
文章目录
A. Filling Diamonds
-
题意
给你一个由 4 n − 2 4n-2 4n−2个三角形组成的菱形图,问你有多少中不同的方案填充菱形。 -
解题思路
我们发现,其有 n n n个竖着的菱形,这些其实就是分割块,由这些分割得来的则是横着的菱形且相邻,所以不难得知,每在一个竖着的菱形放置就会有一种方案,所以答案就是 n n n。 -
AC代码
/**
*@filename:A
*@author: pursuit
*@created: 2021-08-14 21:24
**/
#include <bits/stdc++.h>
#define debug(a) cout << "debug : " << (#a)<< " = " << a << endl
using namespace std;
typedef pair<int,int> pii;
typedef long long ll;
const int N = 1e5 + 10;
const int P = 1e9 + 7;
const int INF = 0x3f3f3f3f;
int t,n;
void solve(){
printf("%d\n", n);
}
int main(){
scanf("%d", &t);
while(t -- ){
scanf("%d", &n);
solve();
}
return 0;
}
B. Sorted Adjacent Differences
-
题意
给你 n n n个整数,重新排列它们使得相邻两数绝对值之差非递减。 -
解题思路
我们从小到大排序次数组,则在数轴上可得到如图:
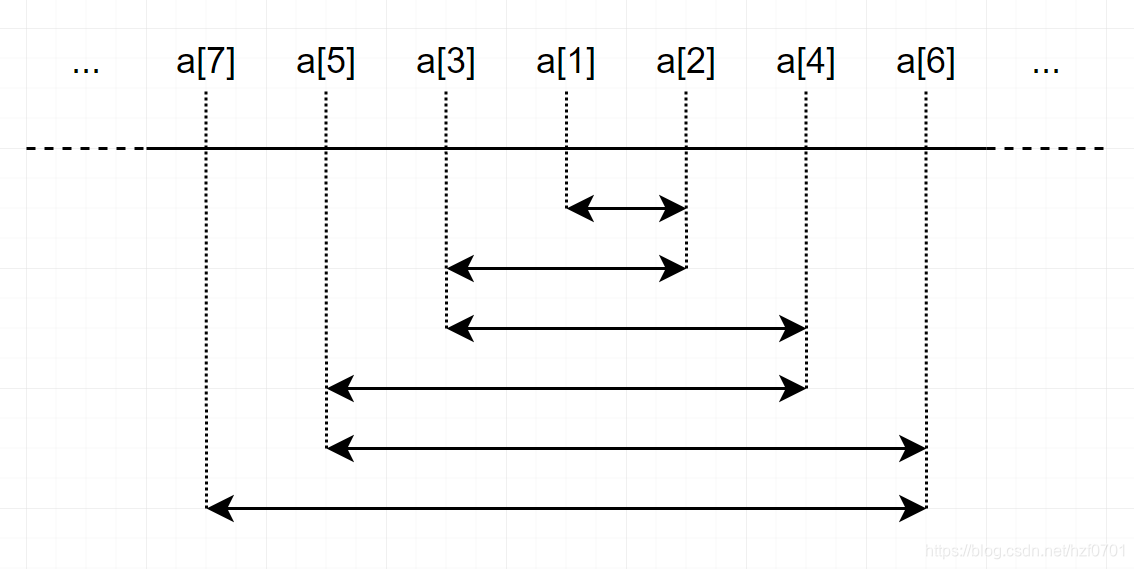
易知,取从中间分开往左右两边去即可。 -
AC代码
/**
*@filename:B
*@author: pursuit
*@created: 2021-08-14 21:30
**/
#include <bits/stdc++.h>
#define debug(a) cout << "debug : " << (#a)<< " = " << a << endl
using namespace std;
typedef pair<int,int> pii;
typedef long long ll;
const int N = 1e5 + 10;
const int P = 1e9 + 7;
const int INF = 0x3f3f3f3f;
int t,n,a[N];
void solve(){
sort(a + 1, a + 1 + n);
int l = n / 2,r = n / 2 + 1;
if(n % 2){
printf("%d ", a[r ++]);
}
while(l >= 1){
printf("%d %d ",a[l],a[r]);
l --,r ++;
}
}
int main(){
scanf("%d", &t);
while(t -- ){
scanf("%d", &n);
for(int i = 1; i <= n; ++ i){
scanf("%d", &a[i]);
}
solve();
}
return 0;
}
C. Powered Addition
-
题意
给你一个 n n n个元素的数组,其中在第 i − t h s e c o n d i-th \ second i−th second时可以为数组中的任意元素增加 2 i − 1 2^{i-1} 2i−1,请你判断需要使得数组呈非递减的最小时间。 -
解题思路
我们知道,随着秒数增加,我们能增长的值也是越来越多。所以我们发现,如果我们抵消了后面数与前面的数的最大差值,那么前面的过程就可以使得数组呈非递减。因为这是需要的最大贡献,前面的秒数则是消除其他的差值。 -
AC代码
/**
*@filename:C
*@author: pursuit
*@created: 2021-08-14 21:36
**/
#include <bits/stdc++.h>
#define debug(a) cout << "debug : " << (#a)<< " = " << a << endl
using namespace std;
typedef pair<int,int> pii;
typedef long long ll;
const int N = 1e5 + 10;
const int P = 1e9 + 7;
const int INF = 0x3f3f3f3f;
int t,n,a[N];
//t秒可以给数组中的任意元素加上2^{t-1}次方。找到与前面差值最大的,它可以了其他就可以了。
int cal(int x){
int res = 0;
while(x){
x /= 2;
res ++;
}
return res;
}
void solve(){
int cnt = 0,minn = a[n];
for(int i = n - 1; i >= 1; -- i){
cnt = max(cnt,a[i] - minn);
minn = min(minn,a[i]);
}
printf("%d\n",cnt == 0 ? 0 : cal(cnt));
}
int main(){
scanf("%d", &t);
while(t -- ){
scanf("%d", &n);
for(int i = 1; i <= n; ++ i){
scanf("%d", &a[i]);
}
solve();
}
return 0;
}
D. Edge Weight Assignment
-
题意
给你一颗 n n n个结点的无向树,你可以给这些边添加权值,范围为 [ 1 , + inf ] [1,+\inf] [1,+inf],使得叶子结点之间的异或路径和为 0 0 0,问边权值的不同数量最小和最大。 -
解题思路
最小情况
若是任意两个叶子结点之间的距离为偶数,则答案为1。因为我们只要在叶子结点中的路径上添上相同的边即可。
而如果存在叶子结点之间的距离为奇数,则答案为3,因为是连通的,且n >= 3,所以当为奇数时,路径长度一定是>1的。
所以如果我们需要使得异或和为0,取相同值明显不行,所以我们需要使得abc = 0,即a ^ b = c,这样才满足条件。
最大情况
我们最大是可以取任何边的,只要满足我们所需的条件即可。不过有一种需要注意的就是当叶子节点之间距离为2,
其边权值只能取相同值异或和才为0。
所以我们需要找出叶子节点和它们之间的距离即可。 -
AC代码
/**
*@filename:D
*@author: pursuit
*@created: 2021-08-15 10:41
**/
#include <bits/stdc++.h>
#define debug(a) cout << "debug : " << (#a)<< " = " << a << endl
using namespace std;
typedef pair<int,int> pii;
typedef long long ll;
const int N = 1e5 + 10;
const int P = 1e9 + 7;
const int INF = 0x3f3f3f3f;
struct node{
int to,next;
}edges[N << 1];
int head[N],tot,in[N];
int depth[N];//深度。
int n,u,v;
int f[N];//统计和叶子结点相邻的次数。
void add(int u,int v){
edges[++tot].to = v;
edges[tot].next = head[u];
head[u] = tot;
}
void dfs(int u,int fu){
int v;
for(int i = head[u]; i; i = edges[i].next){
v = edges[i].to;
if(v == fu)continue;
depth[v] = depth[u] + 1;
dfs(v,u);
}
}
void solve(){
for(int i = 1; i <= n; ++ i){
if(in[i] == 1){
f[edges[head[i]].to] ++;
}
}
dfs(1,0);
int minn = 1,maxx = n - 1;
for(int i = 1; i <= n; ++ i){
maxx -= max(0,f[i] - 1);
}
bool flag1 = false, flag2 = false;
for(int i = 1; i <= n; ++ i){
if(in[i] == 1){
if(depth[i] & 1)
flag1 = true;
else{
flag2 = true;
}
}
}
if(flag1 && flag2)minn = 3;
printf("%d %d\n", minn, maxx);
}
int main(){
scanf("%d", &n);
for(int i = 1; i < n; ++ i){
scanf("%d%d", &u, &v);
add(u,v),add(v,u);
in[u] ++,in[v] ++;
}
solve();
return 0;
}
E. Perfect Triples
-
题意
有一个无穷的元组集,从小到大开始放入。问第 n n n个数是什么。 -
解题思路
打表之后发现,三个数作为数列中的一项,每一段的第一个数以及段长都是公比为4的等比数列。若n%3 = 1,则说明就是每三个数中的第一个数。若n % 2 = ,2,可以看到在第二列中,减去该段的第一个数 * 2,都以 0 2 3 1循环,加一下就即可。若n % 3 = 0,可以看到在第三列中,减去该段的第一个数 * 3,每一位二进制都以0 3 1 2循环。
/**
*@filename:E
*@author: pursuit
*@created: 2021-08-15 12:28
**/
#include <bits/stdc++.h>
#define debug(a) cout << "debug : " << (#a)<< " = " << a << endl
using namespace std;
typedef pair<int,int> pii;
typedef long long ll;
const int N = 1e5 + 10;
const int P = 1e9 + 7;
const int INF = 0x3f3f3f3f;
int t;
ll n;
int f[3][4] = {{0,3,1,2},{},{0,2,3,1}};
ll cal(ll a,ll b){
ll res = 0, p = 1;
if(b == 1)return a;
while(a){
res = res + f[b][a % 4] * p;
a >>= 2;
p <<= 2;
}
return res;
}
void solve(){
ll j = 1,a;
while(j <= n)j <<= 2;//求四进制下的最高位。
j >>= 2;
if(j + 2 >= n)a = j;//判断是否在该行。
else a = j + (n - j) / 3;
printf("%lld\n", cal(a,n % 3));
}
int main(){
scanf("%d", &t);
while(t -- ){
scanf("%lld", &n);
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号