数据结构——红黑树踩坑经历
C++萌新,以此帖总结自己手撕红黑树过程中遇到的一些问题和知识点。
源码:github:https://github.com/uni0ka/RB_Tree
佛系总结,想起来再写
目录:
- 一些资源
- 红黑树特征
- 红黑树核心算法
- 手撕过程中遇到的问题
- 总结
一、一些资源
- 红黑树原理分析: https://zhuanlan.zhihu.com/p/166319823 算法分析写得非常清楚,大量图解和动画方便理解
- 美团技术团队的红黑树剖析及java实现: https://tech.meituan.com/2016/12/02/redblack-tree.html 源码看起来非常舒服
- 园内一位大佬的帖子: https://www.cnblogs.com/skywang12345/p/3245399.html 内容非常全,从介绍到原理到实现都有
- 旧金山大学的数据结构可视化分析工具:https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
二、红黑树特征
关于红黑树的优点和特征,网上有大量资源,不再赘述。
这里记录一个比较冷门的定理证明方法。定理:一棵含有n个节点的红黑树的最大高度是2log(n+1) (本文所有log均以2为底)。证明过程如下:对于一颗红黑树,将null的叶子结点移除,将红色结点全部移除,失去红色父结点的黑色结点接到祖父结点上。在“最糟糕”情况下,红黑树变为一颗满二叉树(此时以剩余的黑色结点数为n),此时高度为log(n+1)。将红色结点补回去,由于红色结点不能相连,则在“最糟糕”情况下,从黑色根结点开始,黑红相间,最后一层为红色(此时以黑色和红色结点总数为n)。这样一来,黑色和红色层数相同,高度变为2倍,为2log(n+1),证毕。
除了常见的五个性质外,还有一些比较重要的特征:(1)含有相同结点的红黑树不是唯一的,但在结点插入和删除顺序一致时,红黑树是唯一的。(2)红黑树的黑树是完全平衡的,这也是红黑树平衡性的来源。(3)可以有连续的黑色结点,但不能有连续的红色结点,否则破坏性质4,这一点有助于理解红黑树结点的插入。(4)若黑色结点为叶子(非nil),则它必定有兄弟结点,否则破坏性质5,这一点有助于理解结点的删除
三、红黑树算法
1.左旋右旋
左旋:
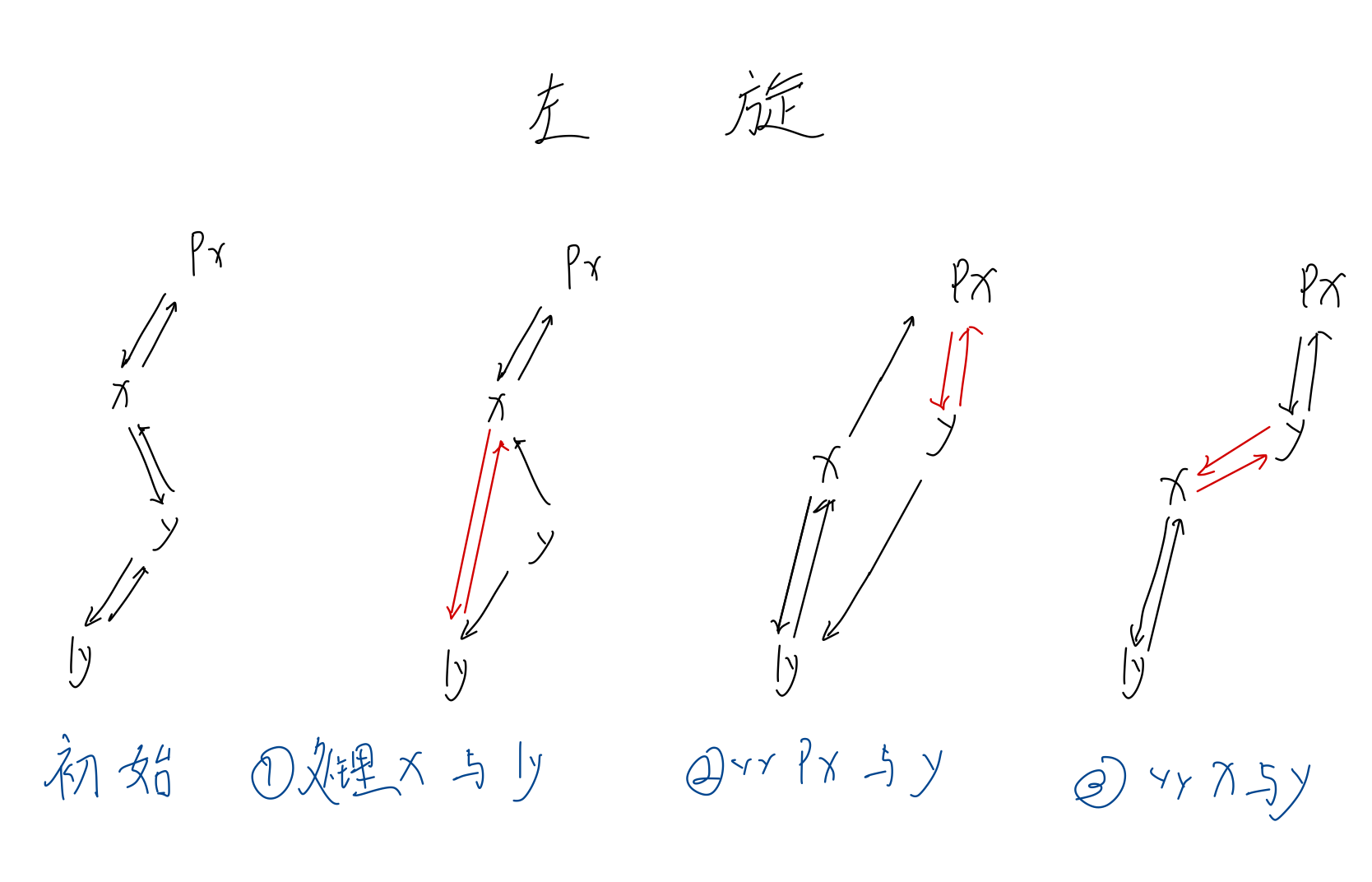
右旋: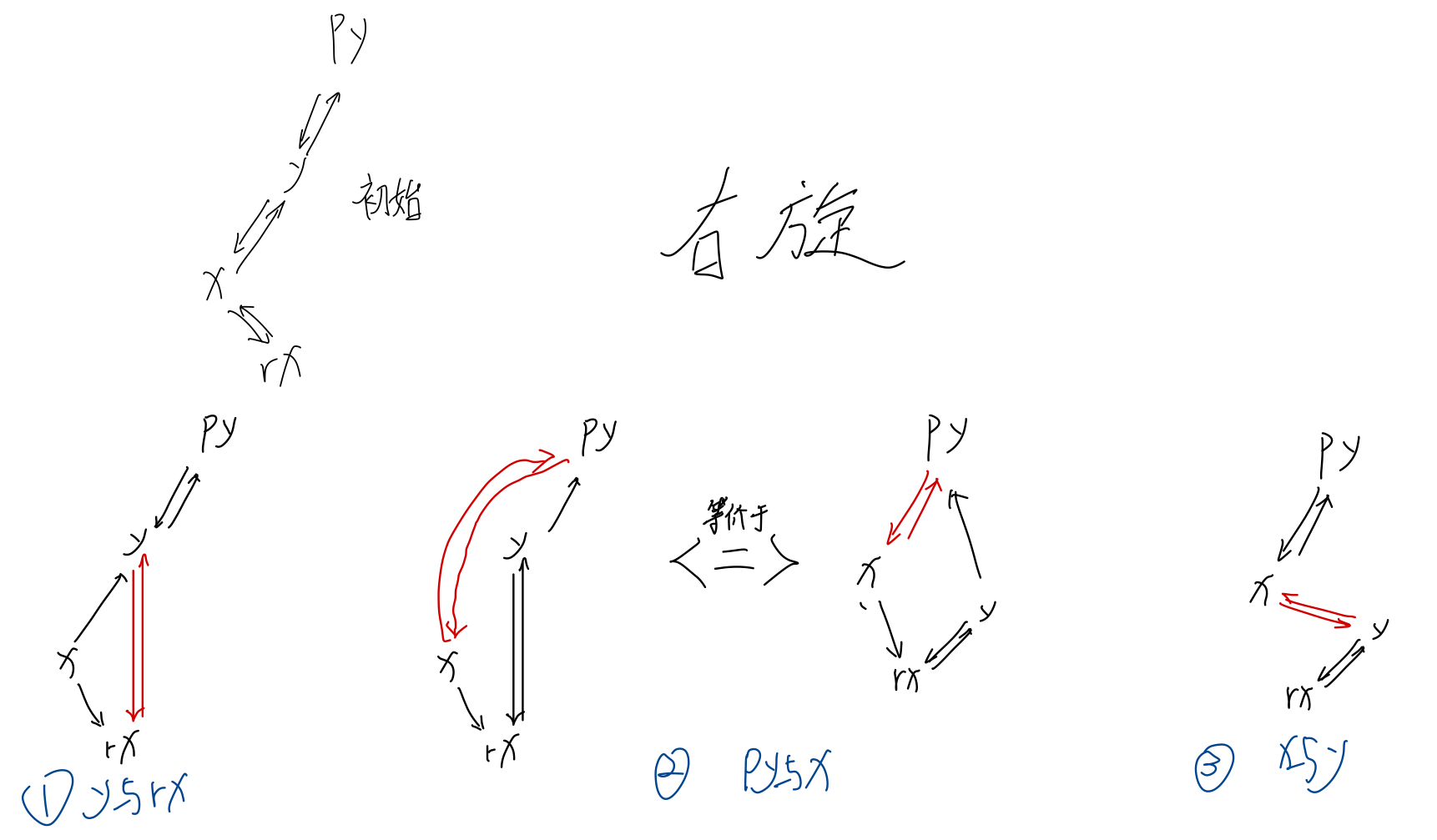
2.插入及插入修正
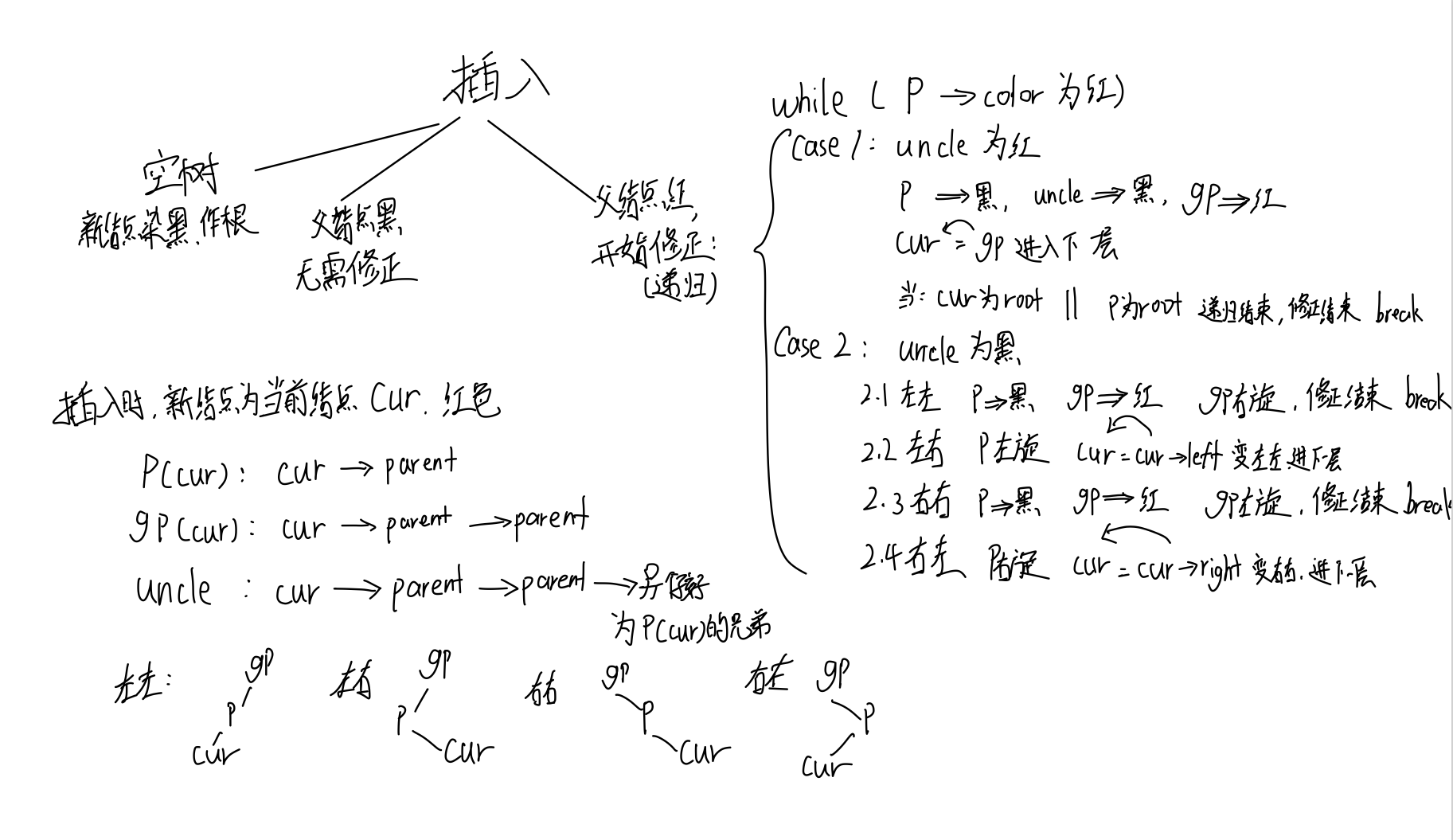
3.删除
通过交换结点值的方式,把删非叶子的情况变为删叶子,也就是找替身。
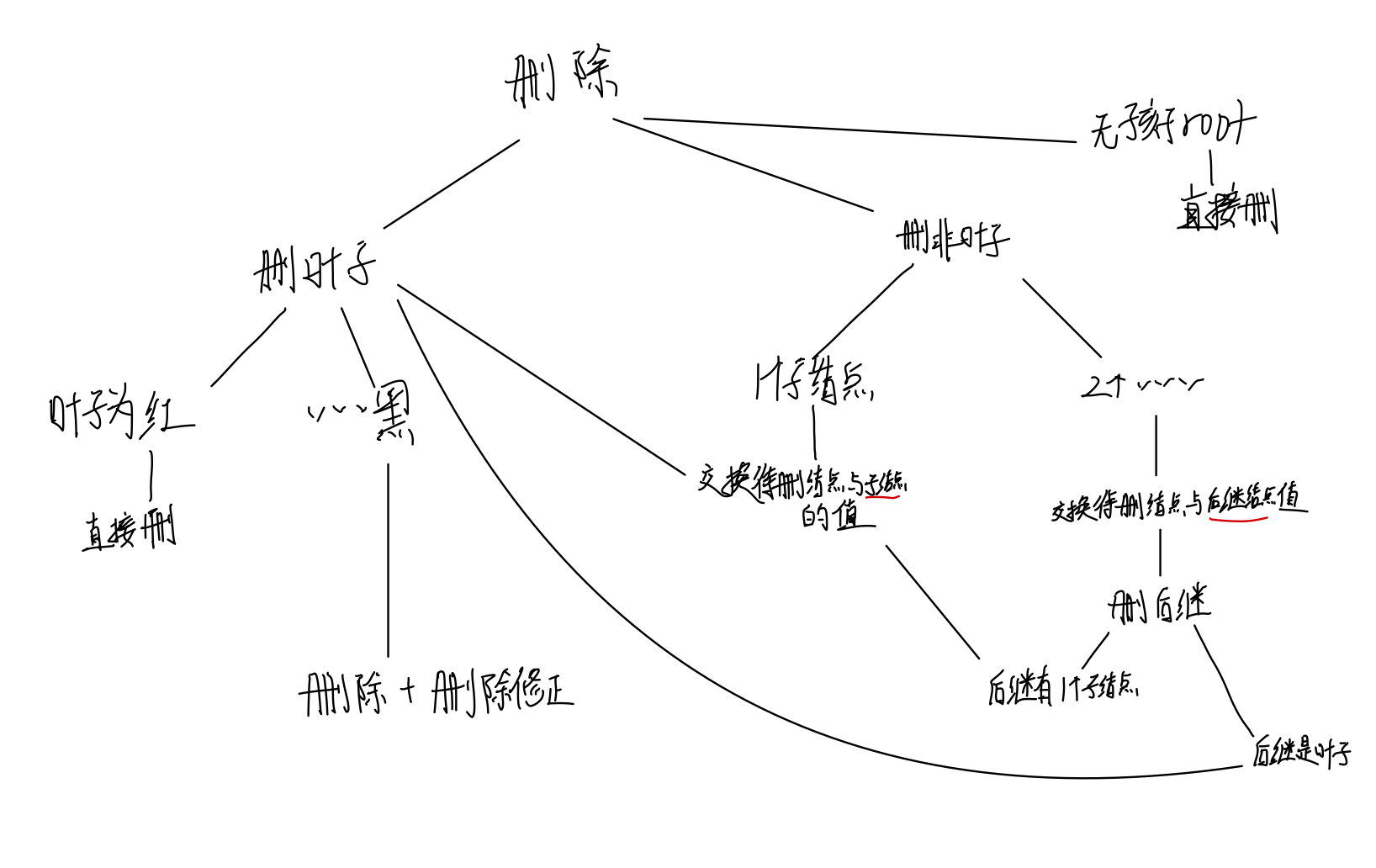
4.删除修正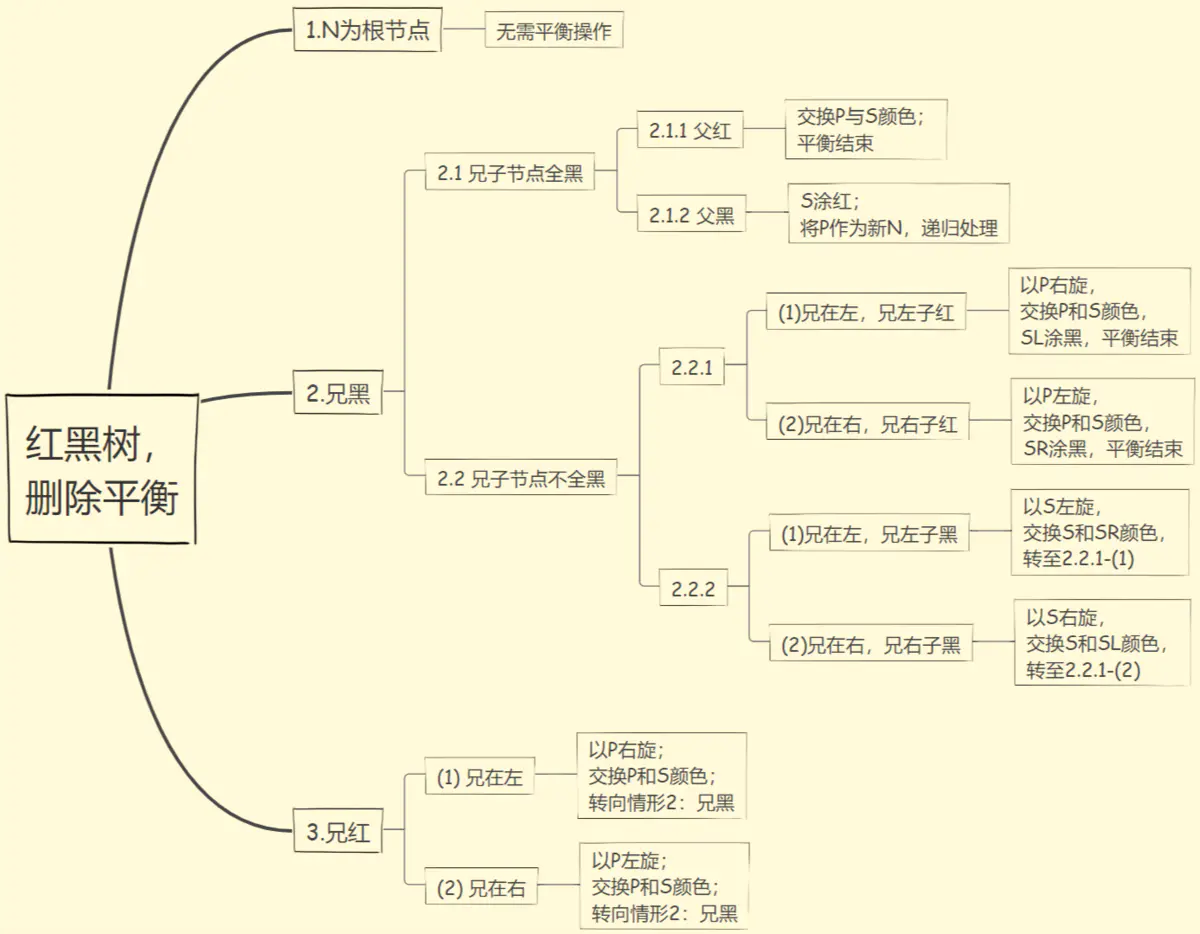
N:当前结点(待删除的结点)
S:兄弟结点 SL:兄弟结点的左孩子 SR:兄弟结点的右孩子
P:父亲结点



 浙公网安备 33010602011771号
浙公网安备 33010602011771号