NOIP2018 提高组 保卫王国

DP，倍增，LCA

算法 1

对于 \(n,m \leq 10\)，这部分可以直接枚举每个点选或不选的情况，时间复杂度为 \(O(2^{n}m)\)。

算法 2

对于 \(n,m \leq 2 \times 10^3\)。

设 \(f(u,0/1)\) 表示选择以 \(u\) 为根的子树，且点 \(u\) 选或不选的最小代价。则

\[f(u,0)= \sum{f(v,1)}\\ f(u,1)=\sum{\min\left(f(v,0),f(v,1)\right)}+p_u \]

其中 \(v\) 表示 \(u\) 的子节点。对于每次询问我们 dp 一次。时间复杂度为 \(O(nm)\)。

算法 3

对于 \(100\%\) 的数据。

考虑一个序列问题。假设一个序列：我们求出了 \(f(i,0/1)\) 表示 \(1 \sim i\)，其中 \(i\) 选或不选的最小代价；\(g(i,0/1)\) 表示 \(i+1 \sim n\) ，其中 \(i\) 选或不选的最小代价。那么 \(i\) 不选的最小代价为 \(\min\left(f(i,0)+g(i,0)\right)\)，\(i\) 选的最小代价为 \(\min(f(i,1)+g(i,1))\)。

对于本题，我们定义：

• \(f(u,0/1)\) 表示选择以 \(u\) 为根的子树，且点 \(u\) 选或不选的最小代价。（与第二部分相同）
• \(g(u,0/1)\) 表示选择整棵树除去以 \(u\) 为根的子树外的所有点，且 \(u\) 选或不选的最小代价。

我们处理出 \(f,g\) 后，当要求 \(u\) 选或不选时，我们能够快速求解。其中，求 \(f\) 的部分与第二部分相同，这里只讲述求 \(g\)。\(g\) 应该从上往下更新，与 \(f\) 相反（考虑上面那个序列问题）。设 \(v\) 表示 \(u\) 的子节点，则：

\[g(v,0)=g(u,1)+f(u,1)-\min\left(f(v,0),f(v,1)\right) \\ g(v,1)=\min\left(g(v,0),g(u,0)+f(u,0)-f(v,1)\right) \]

对于 \(g(v,0)\)，我们需要用以 \(u\) 为根的子树的最小代价减去以 \(v\) 为根的子树的最小代价，以 \(v\) 为根的贡献为 \(\min\left(f(v,0),f(v,1)\right)\)（具体见求 \(f\) 的部分），减去即可。对于 \(g(v,1)\)，\(u\) 可以选或不选，选的情况与 \(g(v,0)\) 相同。

再考虑一个序列问题。这时我们要求 \(i,j\)，两个点分别选或不选时的最小代价。此时，我们可以把整个序列的代价分成三部分：

整个序列的最小代价也就是三个部分加起来，对于蓝和绿的部分，我们已经处理出了 \(f,g\)，现在我们需要求出黄色部分。对于求黄色部分，可以考虑倍增，设 \(h(i,k,0/1,0/1)\) 表示 \(i\) 的状态为选或不选，往后跳 \(2^k\) 步后到达点 \(j\)，\(j\) 的状态为选或不选的最小代价。也就是 \((i,2^k]\) 的最小代价。只需 \(\log n\) 即可求出答案。

回到本题，在本题中也可以这样计算，我们要求了 \(u,v\) 的状态，最小代价为以 \(u\) 为根的子树的最小代价、除去以 \(v\) 为根的子树的最小代价、中间的代价的和。注意，这仅在 \(u,v\) 在同一条链上时。设 \(h(u,k,0/1,0/1)\) 表示 \(u\) 的状态，\(u\) 往上跳 \(2^k\) 步到达点 \(v\) 的状态，以 \(v\) 为根的子树的最小代价减去以 \(u\) 为根的子树的最小代价。

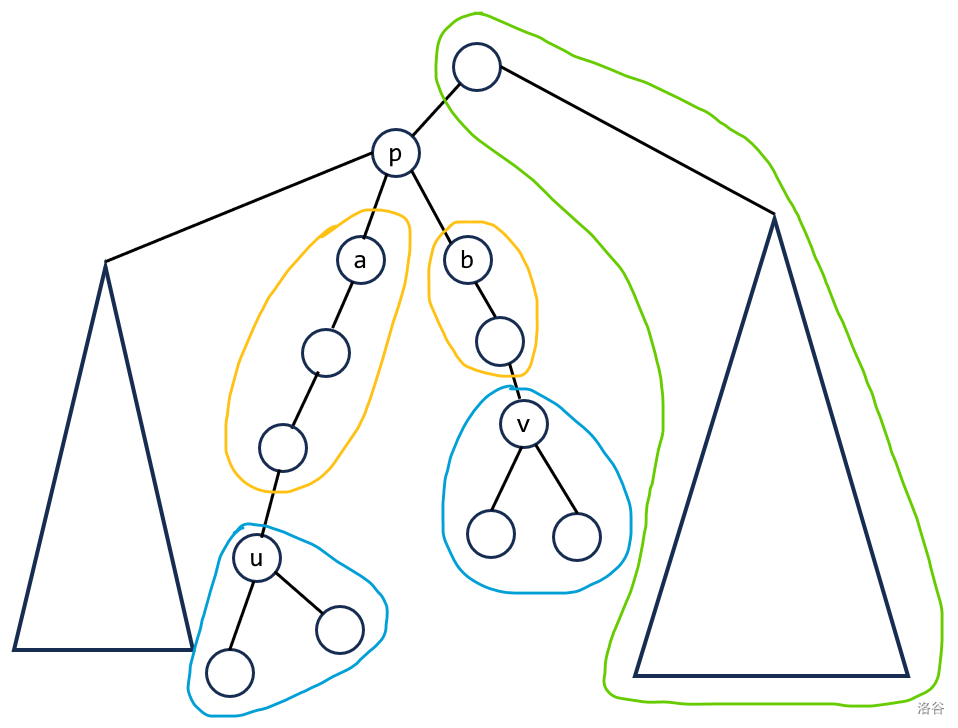
假设 \(u,v\) 不在一条链上，如上图，其中三角形为子树。在这张图上，我们不能像链上那样做，我们从 \(u,v\) 开始往上跳，如上图，到达 \(a,b\)，设它们的最近公共祖先为 \(p\)，则 \(a,b\) 离 \(p\) 仅一步。其中，\(a,b,p\) 的状态并不是固定的，设 \(w_a(0/1)\) 表示以 \(a\) 为根的子树的最小代价，其中 \(a\) 选或不选，\(w_b(0/1)\) 类似。然后分别考虑 \(p\) 选或不选的状态：

• 当不选择 \(p\) 的时候，答案为 \(g(p,0)+f(p,0)-f(a,1)-f(b,1)+w_a(1)+w_b(1)\)。
• 当选择 \(p\) 的时候，答案为 \(g(p,1)+f(p,1)-\min\left(f(a,0),f(a,1)\right)-\min\left(f(b,0),f(b,1)\right)+\min\left(w_a(0),w_a(1)\right)+\min\left(w_b(0),w_b(1)\right)\)。

最后只剩下两个问题了，即求 \(h\) 和 \(w\)。初始化 \(h\) 时，也就是往上跳 \(2^0\) 步，设到达的点为 \(v\)，一共四种情况：

\[h(u,0,0,0)=\infty \\ h(u,0,1,0)=f(v,0)-f(u,1) \\ h(u,0,0,1)=f(v,1)-\min\left(f(u,0),f(u,1)\right) \\ h(u,0,1,1)=f(v,1)-\min\left(f(u,0),f(u,1)\right) \]

其中，\(u,v\) 均不选的情况是不可以的。考虑计算 \(h(u,k,x,y)\)：

\[h(u,k,x,y)=\min\left(h(u,k-1,x,z)+h(p,k-1,z,y)\right) \]

其中 \(p\) 表示 \(u\) 往上跳 \(2^{k-1}\) 步到达的点，\(z\) 表示 \(p\) 的状态。

求 \(w_a,w_b\)，在 \(a,b\) 往上跳的时候，枚举 \(x,y\)，则 \(w_a(y)=\max\left(w_a(x)+h(a,k,x,y)\right)\)，\(w_b\) 相同。

#include <bits/stdc++.h>

using i64 = long long;
const int N = 1e5 + 5, M = 20;

int n, w[N], fa[N][M], depth[N];
i64 f[N][2], g[N][2], h[N][M][2][2];
std::vector<int> adj[N];

void dfs1(int u, int p) {
  fa[u][0] = p;
  depth[u] = depth[p] + 1;
  for (int i = 1; i <= std::__lg(depth[u]); i++) {
    fa[u][i] = fa[fa[u][i - 1]][i - 1];
  }
  for (auto v : adj[u]) {
    if (v == p) {
      continue;
    }
    dfs1(v, u);
  }
}

void dfs2(int u, int p) {
  f[u][1] = w[u];
  for (auto v : adj[u]) {
    if (v == p) {
      continue;
    }
    dfs2(v, u);
    f[u][0] += f[v][1];
    f[u][1] += std::min(f[v][0], f[v][1]);
  }
}

void dfs3(int u, int p) {
  for (auto v : adj[u]) {
    if (v == p) {
      continue;
    }
    g[v][0] = g[u][1] + f[u][1] - std::min(f[v][0], f[v][1]);
    g[v][1] = std::min(g[v][0], g[u][0] + f[u][0] - f[v][1]);
    dfs3(v, u);
  }
}

void dfs4(int u, int p) {
  for (auto v : adj[u]) {
    if (v == p) {
      continue;
    }
    h[v][0][1][0] = f[u][0] - f[v][1];
    h[v][0][0][1] = f[u][1] - std::min(f[v][0], f[v][1]);
    h[v][0][1][1] = f[u][1] - std::min(f[v][0], f[v][1]);
    for (int k = 1; k <= std::__lg(depth[v]); k++) {
      for (int x = 0; x < 2; x++) {
        for (int y = 0; y < 2; y++) {
          for (int z = 0; z < 2; z++) {
            h[v][k][x][y] = std::min(h[v][k][x][y], h[v][k - 1][x][z] + h[fa[v][k - 1]][k - 1][z][y]);
          }
        }
      }
    }
    dfs4(v, u);
  }
}

i64 LCA(int a, int x, int b, int y) {
  while (depth[a] < depth[b]) {
    std::swap(a, b);
    std::swap(x, y);
  }
  if (!x && !y && fa[a][0] == b) {
    return -1;
  }
  i64 wa[2], wb[2], ta[2], tb[2];
  memset(wa, 0x3f, sizeof(wa));
  memset(wb, 0x3f, sizeof(wb));
  wa[x] = f[a][x], wb[y] = f[b][y];
  while (depth[a] > depth[b]) {
    int k = std::__lg(depth[a] - depth[b]);
    memset(ta, 0x3f, sizeof(ta));
    for (int u = 0; u < 2; u++) {
      for (int v = 0; v < 2; v++) {
        ta[v] = std::min(ta[v], wa[u] + h[a][k][u][v]);
      }
    }
    memcpy(wa, ta, sizeof(wa));
    a = fa[a][k];
  }
  if (a == b) {
    return wa[y] + g[b][y];
  }
  for (int i = std::__lg(depth[a]); i >= 0; i--) {
    if (fa[a][i] != fa[b][i]) {
      memset(ta, 0x3f, sizeof(ta));
      memset(tb, 0x3f, sizeof(tb));
      for (int u = 0; u < 2; u++) {
        for (int v = 0; v < 2; v++) {
          ta[v] = std::min(ta[v], wa[u] + h[a][i][u][v]);
          tb[v] = std::min(tb[v], wb[u] + h[b][i][u][v]);
        }
      }
      memcpy(wa, ta, sizeof(wa));
      memcpy(wb, tb, sizeof(wb));
      a = fa[a][i], b = fa[b][i];
    }
  }
  int lca = fa[a][0];
  i64 res1 = g[lca][0] + f[lca][0] - f[a][1] - f[b][1] + wa[1] + wb[1];
  i64 res2 = g[lca][1] + f[lca][1] - std::min(f[a][0], f[a][1]) - std::min(f[b][0], f[b][1]) + std::min(wa[0], wa[1]) + std::min(wb[0], wb[1]);
  return std::min(res1, res2);
}

int main() {
  std::ios::sync_with_stdio(false);
  std::cin.tie(nullptr);
  int q;
  std::string opt;
  std::cin >> n >> q >> opt;
  for (int i = 1; i <= n; i++) {
    std::cin >> w[i];
  }
  for (int i = 1; i < n; i++) {
    int u, v;
    std::cin >> u >> v;
    adj[u].push_back(v);
    adj[v].push_back(u);
  }
  dfs1(1, 0); // 求 fa 和 depth
  dfs2(1, 0); // 求 f
  dfs3(1, 0); // 求 g
  memset(h, 0x3f, sizeof(h));
  dfs4(1, 0); // 求 h
  while (q--) {
    int a, x, b, y;
    std::cin >> a >> x >> b >> y;
    std::cout << LCA(a, x, b, y) << '\n';
  }
  return 0;
}