小清新笔记
小清新题
(经过一天的小清新题的洗礼,感觉整个人的都可以入土了)小清新题给人的第一感觉,哇!这题干好短啊,也没太多的要维护的东西,这题肯定很简单吧。理解完题意后发现,什么抽象题,根本没思路,(使用跳题dp)。虽然写完了zzz学长上课讲的那些题,感觉做小清新题的时候还是有思路但不多,正好今天写不下去题了,就来稍微整理一下。
例题一:
Number of Components
题面翻译
有一条\(n(1 \leq n \leq 10^5)\)个节点的链,编号相邻节点有边,每个点一个权值\(a_i(1 \leq a_i \leq n)\),\(f(l,r)\)定义为权值在\([l,r]\)的点中的连通块数量求\(\sum_{l=1}^{n}\sum_{r=l}^{n}f(l,r)\)
样例 #1
样例输入 #1
3
2 1 3
样例输出 #1
7
样例 #2
样例输入 #2
4
2 1 1 3
样例输出 #2
11
分析:
首先对于这个题,我们第一眼就有一个非常暴力的做法,那就是直接暴力美剧每个权值区间,然后在暴力查一遍所有的连通块,这显然是过不去的。我们考虑怎么去优化,首先有一个学过图论的人都知道一个公式,那就是 \(点数 - 边数 = 联通块的数量\),那么我们现在就转换成了如何快速求点数和边数,我们可以先单独考虑每个点的贡献,对于每一个点,他的贡献显然是 \(a[i] \times (n-a[i] + 1)\),只有 \(L \geq a[i]\) 并且 \(R \leq (n - a[i] + 1)\) 中,这个点才会被选中。我们再接着来看边的情况,对于一条边,他的左右端点为 \(u\) 和 \(v\),那么根据点的关系,我们可以推出边的贡献为 \(\min(a[u], a[v]) \times (n - \max(a[u], a[v]) + 1)\),因为我们要保证区间的左端点是小于等于最小的那个值,右端点要在最大的值的右边,既然我们都算出了点和边的贡献,我们也就可以把这道题给切了。(我记得是得开long long ,要不然会爆掉)
#include <cstring>
#include <iostream>
#include <algorithm>
#define int long long
namespace read_write
{
template <typename T>
inline void read(T &x)
{
x = 0;
T f = 1;
char ch = getchar();
while (ch > '9' || ch < '0')
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
x = x * 10 + ch - '0', ch = getchar();
x *= f;
return;
}
template <typename T>
inline void write(T x)
{
if (x < 0)
{
x = -x;
putchar('-');
}
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
template <typename T>
T max(T x, T y)
{
return x > y ? x : y;
}
template <typename T>
T min(T x, T y)
{
return x > y ? y : x;
}
template <typename T>
void swap(T &a, T &b)
{
T tem = b;
b = a;
a = tem;
}
}
namespace Solve
{
using namespace read_write;
const int N = 1e6 + 10;
int n;
int a[N], sum1, sum2;
void solve()
{
read(n);
for(int i = 1 ; i <= n ; ++ i)
read(a[i]);
for(int i = 1 ; i <= n ; ++ i)
{
sum1 += a[i] * (n - a[i] + 1); //计算所有的点的贡献
if(i == n)
continue;
sum2 += min(a[i], a[i + 1]) * (n - max(a[i], a[i + 1]) + 1); //计算所有的边的贡献
}
write(sum1 - sum2);
}
}
signed main()
{
//freopen("test.in", "r", stdin);
//freopen("test.out", "w", stdout);
Solve::solve();
return 0;
}
例题二:
赛车游戏
题目描述
R 君和小伙伴打算一起玩赛车。但他们被老司机 mocania 骗去了秋名山。
秋名山上有 \(n\) 个点和 \(m\) 条边,R 君和他的小伙伴要从点 \(1\) 出发开往点 \(n\),每条边都有一个初始的方向。老司机 mocania 拿到了秋名山的地图但却不知道每条路有多长。显然,为了赛车游戏的公平,每条 \(1\) 到 \(n\) 的路径应当是等长的。mocania 想,我就随便给边标上一个 \(1...9\) 的长度,反正傻傻的 R 君也看不出来。
可 mocania 的数学不大好,不知道怎么给边标长度,只能跑来请教你这个 OI 高手了。
输入格式
第一行两个整数 \(n,m\)。
接下来 \(m\) 行,每行两个整数 \(u,v\),表示一条从 \(u\) 到 \(v\) 的有向边。
输出格式
如果无解或者不存在 \(1\) 到 \(n\) 的路径直接输出一个 \(-1\)。
如果有解第一行输出两个数 \(n,m\),和输入文件中给出的相同。
借下来 \(m\) 行,每行三个整数 \(u,v,w\),表示把从 \(u\) 到 \(v\) 的路径的长度设置为 \(w\),其中 \(w\) 是一个 \(1\sim 9\) 的整数。要求所有边的出现顺序和题目中给出的相同。
样例 #1
样例输入 #1
10 10
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
1 10
样例输出 #1
10 10
1 2 1
2 3 1
3 4 1
4 5 1
5 6 1
6 7 1
7 8 1
8 9 1
9 10 1
1 10 9
提示
数据范围
本题启用 Special Judge 和 Subtask。
Subtask #1(\(30\) 分):\(n \leq 10\),\(m \leq 20\);
Subtask #2(\(30\) 分):\(n \leq 100\),\(m \leq 200\);
Subtask #3(\(40\) 分):\(n \leq 1000\),\(m \leq 2000\)。
保证数据中不会出现重边,自环。
分析:
首先,题干说的是要求 \(1\) 到 \(n\) 的所有路径都是相同长度的,那么对于路径外的边我们随便设即可,同时我们观察到题干中对于边的长度给出了限制,长度都在 \(1\) 到 \(9\) 之间,我们设 \(dis[i]\) 为 \(1\) 到 \(i\) 的距离,然后我们会发现,对于一条边连接 \(u\) 和 \(v\),都必须要满足 \(1 \leq dis[u] - dis[v] \leq 9\),然后我们移一下项之后会发现这就是个差分约束系统,那么我们直接跑 \(spfa\) 判断一下有没有负环,最后在输出一下合法边权就行了。有一个小细节就是直接跑 \(spfa\) 好像跑不过去,那么我们可以正着跑一次,反着跑一次,处理出来在路径上的边,然后建个新图,在新图上跑 \(spfa\)。
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
namespace read_write
{
template <typename T>
inline void read(T &x)
{
x = 0;
T f = 1;
char ch = getchar();
while (ch > '9' || ch < '0')
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
x = x * 10 + ch - '0', ch = getchar();
x *= f;
return;
}
template <typename T>
inline void write(T x)
{
if (x < 0)
{
x = -x;
putchar('-');
}
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
template <typename T>
T max(T x, T y)
{
return x > y ? x : y;
}
template <typename T>
T min(T x, T y)
{
return x > y ? y : x;
}
template <typename T>
void swap(T &a, T &b)
{
T tem = b;
b = a;
a = tem;
}
}
namespace Solve
{
using namespace read_write;
const int N = 1e6 + 10, INF = 0x3f3f3f3f;
int n, m, times[N], dis[N];
int post[N], rev[N], h[N], cnt, idx;
bool st1[N], st2[N], st[N], vis[N];
struct Edge
{
int ne, v, w;
int rev_ne, rev_v;
} e[N];
struct Line
{
int x, y;
} line[N];
void add(int u, int v)
{
e[++ cnt].v = v, e[cnt].ne = post[u], post[u] = cnt;
e[cnt].rev_ne = rev[v], e[cnt].rev_v = u, rev[v] = cnt;
}
void add(int u, int v, int w)
{
e[++ idx].v = v, e[idx].w = w, e[idx].ne = h[u], h[u] = idx;
}
inline void dfs1(int x) //正着跑
{
st1[x] = true;
for(int i = post[x] ; i ; i = e[i].ne)
{
int v = e[i].v;
if(!st1[v])
dfs1(v);
}
}
inline void dfs2(int x) //反着跑
{
st2[x] = true;
for(int i = rev[x] ; i ; i = e[i].rev_ne)
{
int v = e[i].rev_v;
if(!st2[v])
dfs2(v);
}
}
void spfa()
{
std::queue<int> q;
//memset(dis, INF, sizeof(dis));
q.push(1), vis[1] = true, dis[1] = 0, times[1] = 1;
while(!q.empty())
{
int t = q.front();
q.pop(), vis[t] = false;
for(int i = h[t] ; i ; i = e[i].ne)
{
int v = e[i].v;
if(dis[v] > dis[t] + e[i].w)
{
dis[v] = dis[t] + e[i].w;
if(!vis[v])
{
if(times[v] == n)
{
puts("-1");
exit(0);
}
q.push(v), vis[v] = true;
++ times[v];
}
}
}
}
if(dis[n] == INF)
{
puts("-1");
exit(0);
}
}
void solve()
{
read(n), read(m);
for(int i = 1 ; i <= m ; ++ i)
{
int x, y;
read(x), read(y);
add(x, y);
line[i] = {x, y};
}
dfs1(1), dfs2(n);
for(int i = 1 ; i <= n ; ++ i)
st[i] = st1[i] & st2[i], dis[i] = INF;
idx = 0;
for(int i = 1 ; i <= m ; ++ i)
{
if(st[line[i].x] && st[line[i].y])
add(line[i].x, line[i].y, 9), add(line[i].y, line[i].x, -1);
}
spfa();
write(n), putchar(' '), write(m), puts("");
for(int i = 1 ; i <= m ; ++ i)
{
write(line[i].x), putchar(' '), write(line[i].y), putchar(' ');
if(!st[line[i].x] || !st[line[i].y])
write(1);
else
write(dis[line[i].y] - dis[line[i].x]);
puts("");
}
}
}
int main()
{
//freopen("test.in", "r", stdin);
//freopen("test.out", "w", stdout);
Solve::solve();
return 0;
}
例题三
Kay and Snowflake
题面翻译
输入一棵树,判断每一棵子树的重心是哪一个节点.
样例 #1
样例输入 #1
7 4
1 1 3 3 5 3
1
2
3
5
样例输出 #1
3
2
3
6
提示
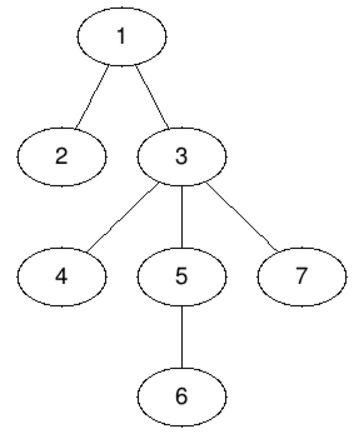
分析:
首先对于每次询问我们都暴力的求一遍,复杂度是非常高的,然后我们得考虑一些更快速的求子树的重心的方法,我们都知道重心的定义,然后我们结合定义就可以差不多有一个猜想,就是假如当前我们从一个节点推他子树的重心,那么重心应该是在这个点到他的重儿子的路径上,为什么因为如果当前节点不是重心,你往轻儿子走只会让答案变的更劣,一直往重儿子走才行,那么这道题想到这里也就差不多切了。
#include <cstring>
#include <iostream>
#include <algorithm>
namespace read_write
{
template <typename T>
inline void read(T &x)
{
x = 0;
T f = 1;
char ch = getchar();
while (ch > '9' || ch < '0')
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
x = x * 10 + ch - '0', ch = getchar();
x *= f;
return;
}
template <typename T>
inline void write(T x)
{
if (x < 0)
{
x = -x;
putchar('-');
}
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
template <typename T>
T max(T x, T y)
{
return x > y ? x : y;
}
template <typename T>
T min(T x, T y)
{
return x > y ? y : x;
}
template <typename T>
void swap(T &a, T &b)
{
T tem = b;
b = a;
a = tem;
}
}
namespace Solve
{
using namespace read_write;
const int N = 1e6 + 10;
int n, m;
int h[N], siz[N], idx;
int fa[N], max_siz[N], ans[N];
struct Edge
{
int ne, v;
} e[N];
void add(int u, int v)
{
e[++ idx].v = v, e[idx].ne = h[u], h[u] = idx;
}
void dfs(int u, int fath)
{
int mx = 0, id = 0;
siz[u] = 1, fa[u] = fath;
for(int i = h[u] ; i ; i = e[i].ne)
{
int v = e[i].v;
if(v == fath)
continue;
dfs(v, u);
siz[u] += siz[v];
if(siz[v] > mx)
mx = siz[v], id = v;
}
max_siz[u] = mx;
if(max_siz[u] * 2 < siz[u])
ans[u] = u;
else
{
int pos = ans[id];
while(fa[pos] && max(max_siz[pos], siz[u] - siz[pos]) > max(max_siz[fa[pos]], siz[u] - siz[fa[pos]]))
pos = fa[pos];
ans[u] = pos;
}
}
void solve()
{
read(n), read(m);
for(int i = 2 ; i <= n ; ++ i)
{
int x;
read(x);
add(x, i);
}
dfs(1, 0);
while(m --)
{
int x;
read(x);
write(ans[x]), puts("");
}
}
}
int main()
{
Solve::solve();
return 0;
}
例题四
Complicated Computations
题面翻译
求一个数列的所有连续子数列的 mex 值的 mex(mex:对于一个序列,这个序列中没出现的最小的正整数)
样例 #1
样例输入 #1
3
1 3 2
样例输出 #1
3
样例 #2
样例输入 #2
5
1 4 3 1 2
样例输出 #2
6
分析
我们手模一下第二个样例,(因为第一个样例实在是太弱了!!!)我们如果当前点的值为 \(a[i]\),那么 \(a[i]\) 能成为 \(mex\) 的位置就只有所有值为 \(a[i]\) 的位置,然后我们就依次递推,枚举 \(mex\) 要是没有有个位置没有,那么我们就直接输出这个 \(mex\) 即可,对于给位置上加数,我们可以整个主席树来维护。
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
namespace read_write
{
template <typename T>
inline void read(T &x)
{
x = 0;
T f = 1;
char ch = getchar();
while (ch > '9' || ch < '0')
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
x = x * 10 + ch - '0', ch = getchar();
x *= f;
return;
}
template <typename T>
inline void write(T x)
{
if (x < 0)
{
x = -x;
putchar('-');
}
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
template <typename T>
T max(T x, T y)
{
return x > y ? x : y;
}
template <typename T>
T min(T x, T y)
{
return x > y ? y : x;
}
template <typename T>
void swap(T &a, T &b)
{
T tem = b;
b = a;
a = tem;
}
}
namespace Solve
{
using namespace read_write;
const int N = 1e6 + 10;
int n, m, cnt;
int a[N], rt[N], idx;
std::vector<int> col[N];
bool st[N];
struct Question
{
int l, r, val;
bool operator < (const Question&a) const {return r < a.r;}
} q[N];
void New(int l, int r, int w)
{
if(l > r)
return ;
q[++ idx].l = l, q[idx].r = r, q[idx].val = w;
}
struct Tree
{
int l, r, val;
} tr[N << 1];
void pushup(int u)
{
tr[u].val = min(tr[tr[u].l].val, tr[tr[u].r].val);
}
void insert(int &u, int last, int l, int r, int p, int k)
{
u = ++ cnt;
tr[u] = tr[last];
if(l == r)
{
tr[u].val = k;
return ;
}
int mid = l + r >> 1;
if(p <= mid)
insert(tr[u].l, tr[last].l, l, mid, p, k);
else
insert(tr[u].r, tr[last].r, mid + 1, r, p, k);
pushup(u);
}
int query(int u, int l, int r, int k)
{
if(l == r)
return l;
int mid = l + r >> 1;
if(tr[tr[u].l].val < k)
return query(tr[u].l, l, mid, k);
else
return query(tr[u].r, mid + 1, r, k);
}
void solve()
{
read(n);
for(int i = 1 ; i <= n ; ++ i)
read(a[i]), col[a[i]].push_back(i);
for(int i = 1 ; i <= n ; ++ i)
{
for(int j = 0 ; j < col[i].size() ; ++ j)
{
if(j == 0)
New(1, col[i][j] - 1, i);
else
New(col[i][j - 1] + 1, col[i][j] - 1, i);
}
if(col[i].size())
New(col[i][col[i].size() - 1] + 1, n, i);
}
for(int i = 1 ; i <= n ; ++ i)
insert(rt[i], rt[i - 1], 1, n + 1, a[i], i);
rt[n + 1] = rt[n];
for(int i = 1 ; i <= idx ; ++ i)
{
int l = q[i].l, r = q[i].r, v = q[i].val;
if(query(rt[r], 1, n + 1, l) == v)
st[v] = true;
}
for(int i = 1 ; i <= n + 2 ; ++ i)
{
if(query(rt[n + 1], 1, n + 1, 1) == i)
st[i] = true;
}
for(int i = 1 ; i <= n + 2 ; ++ i)
if(!st[i])
write(i), exit(0);
}
}
int main()
{
Solve::solve();
return 0;
}
例题五
[国家集训队] 阿狸和桃子的游戏
题目描述
阿狸和桃子正在玩一个游戏,游戏是在一个带权图G=(V, E)上进行的,设节点权值为w(v),边权为c(e)。游戏规则是这样的:
-
阿狸和桃子轮流将图中的顶点染色,阿狸会将顶点染成红色,桃子会将顶点染成粉色。已经被染过色的点不能再染了,而且每一轮都必须给一个且仅一个顶点染色。
-
为了保证公平性,节点的个数N为偶数。
-
经过N/2轮游戏之后,两人都得到了一个顶点集合。对于顶点集合S,得分计算方式为
由于阿狸石头剪子布输给了桃子,所以桃子先染色。两人都想要使自己的分数比对方多,且多得越多越好。如果两人都是采用最优策略的,求最终桃子的分数减去阿狸的分数。
输入格式
输入第一行包含两个正整数N和M,分别表示图G的节点数和边数,保证N一定是偶数。
接下来N+M行。
前N行,每行一个整数w,其中第k行为节点k的权值。
后M行,每行三个用空格隔开的整数a b c,表示一条连接节点a和节点b的边,权值为c。
输出格式
输出仅包含一个整数,为桃子的得分减去阿狸的得分。
样例 #1
样例输入 #1
4 4
6
4
-1
-2
1 2 1
2 3 6
3 4 3
1 4 5
样例输出 #1
3
提示
数据规模和约定
对于40%的数据,1 ≤ N ≤ 16。
对于100%的数据,1 ≤ N ≤ 10000,1 ≤ M ≤ 100000,-10000 ≤ w , c ≤ 10000。
分析:
对于这道题我们会发现计算点权非常好计算,但是有了边权就显得非常难计算,这时,充分发挥自己的智慧,会想到之前我们做树剖题维护边权的时候都会把边权给转换成点权,然后我们想一想这道题能不能也把边权拆成点权呢?显然是可以的,为什么呢?
我们考虑将边权一分为二扔到两个端点上,由于我们最终求的是差值,所以,对于一条边,如果一个人只拿了一半,那么让最后做差时,其实会相互抵消,也就不会在最终的答案中产生这个贡献,所以这个拆边权的策略的正确性是能保证的,然后我们就拆完之后直接 \(sort\) 一下不就能直接计算答案了吗。还有要注意排序的方向性,因为每个人是优先选择大的。
#include <cstring>
#include <iostream>
#include <algorithm>
namespace read_write
{
template <typename T>
inline void read(T &x)
{
x = 0;
T f = 1;
char ch = getchar();
while (ch > '9' || ch < '0')
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
x = x * 10 + ch - '0', ch = getchar();
x *= f;
return;
}
template <typename T>
inline void write(T x)
{
if (x < 0)
{
x = -x;
putchar('-');
}
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
template <typename T>
T max(T x, T y)
{
return x > y ? x : y;
}
template <typename T>
T min(T x, T y)
{
return x > y ? y : x;
}
template <typename T>
void swap(T &a, T &b)
{
T tem = b;
b = a;
a = tem;
}
}
namespace Solve
{
using namespace read_write;
const int N = 1e6 + 10;
int n, m;
double w[N], sum1, sum2;
bool cmp(double a, double b)
{
return a > b;
}
void solve()
{
read(n), read(m);
for(int i = 1 ; i <= n ; ++ i)
read(w[i]);
for(int i = 1 ; i <= m ; ++ i)
{
int a, b, v;
read(a), read(b), read(v);
w[a] += (double) v / 2 * 1.0;
w[b] += (double) v / 2 * 1.0;
}
std::sort(w + 1, w + n + 1, cmp);
for(int i = 1 ; i <= n ; ++ i)
{
if(i & 1)
sum1 += w[i];
else
sum2 += w[i];
}
write(int(sum1 - sum2));
}
}
int main()
{
Solve::solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号