P1502 窗口的星星 题解

窗口的星星

前置知识：扫描线

输入格式

本题有多组数据，第一行为 \(T\)，表示有 \(T\) 组数据。

对于每组数据：

第一行 \(3\) 个整数 \(n,W,H\) 表示有 \(n\) 颗星星，窗口宽为 \(W\)，高为 \(H\)。

接下来 \(n\) 行，每行三个整数 \(x_i,y_i,l_i\) 表示星星的坐标在 \((x_i,y_i)\)，亮度为 \(l_i\)。

输出格式

\(T\) 个整数，表示每组数据中窗口星星亮度总和的最大值。

分析：

我们先看这个题他是给你一个大小固定的窗口，然后让你尽可能多的圈住更多的星星的权值。

我们很快就会有一种很暴力的思路，那就是我们可以对于每一个星星，以它为边界构造那个窗口，然后遍历其他的星星是否在这里面，然后求一下权值，那么复杂度显然是 \(O(N^2T)\) 。显然是不能过的。那么我们就只能另辟奇径了。

我们先画个图。

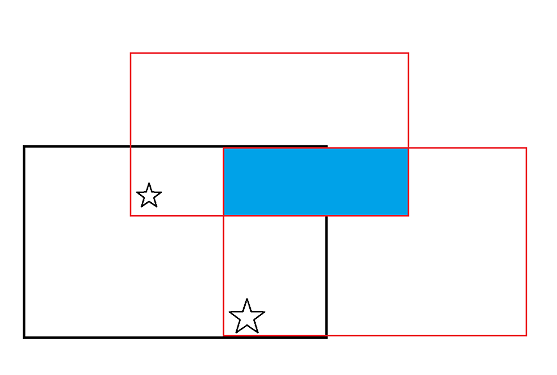
我们会发现，如果是给定一个窗口，那么同窗口的星星所扩展出的矩形就一定会又交集，为图中的蓝色部分，因为我们的星星是可以向上扩展高为窗口宽的矩形，那么两个星星就构成的矩形一定会产生交集，那么我们现在再考虑，此时如果我们能够求出最大的矩形的组合体的面积，然后再求一下区间的最值不就是答案吗。这里需要感性的理解一下，因为我们可以在更新块的时候求出最大值。

那么求这个面积的方法是什么。那必然就是扫描线！！！

记得离散化因为这个坐标给的实在是太大了。

下面是代码实现

#include <iostream>
#include <algorithm>
#include <queue>
#include <cstring>

#define int long long

using namespace std;

inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while(ch > '9' || ch < '0')
    {
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
        x = x * 10 + ch - '0', ch = getchar();
    return x * f;
}

inline void write(int x)
{
    if(x < 0)
    {
        x = -x;
        putchar('-');
    }
    if(x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}

const int N = 2e5 + 10;

int t;
int n, h, w;
int val[N];

struct Tree   //存放每个矩形的上底和下底
{
    int l, r, h, val;
    bool operator < (const Tree& a)
    {
        if(h != a.h)
            return h < a.h;
        return val > a.val;
    }
} Tr[N << 2];

struct SegmentTree   //扫描线
{
    int l, r, mx, tag;
} tr[N << 2];

void ms()
{
    memset(tr, 0, sizeof (tr));
    memset(Tr, 0, sizeof (Tr));
}

void pushup(int u)
{
    tr[u].mx = max(tr[u << 1].mx, tr[u << 1 | 1].mx);
}

void build(int u, int l, int r)
{
    tr[u].l = l, tr[u].r = r, tr[u].mx = tr[u].tag = 0;
    if(l == r)
        return;
    int mid = (l + r) >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}

void pushdown(int u)
{
    tr[u << 1].mx += tr[u].tag;
    tr[u << 1 | 1].mx += tr[u].tag;
    tr[u << 1].tag += tr[u].tag;
    tr[u << 1 | 1].tag += tr[u].tag;
    tr[u].tag = 0;
}

void modify(int u, int L, int R, int k)
{
    int l = tr[u].l, r = tr[u].r;
    if(L <= l && R >= r)
    {
        tr[u].mx += k;
        tr[u].tag += k;
        return ;
    }
    pushdown(u);
    int mid = (l + r) >> 1;
    if(L <= mid)
        modify(u << 1, L, R, k);
    if(R > mid)
        modify(u << 1 | 1, L, R, k);
    pushup(u);
}

signed main()
{
    t = read();

    while(t -- )
    {
        ms();

        n = read(), w = read(), h = read();
        for(register int i = 1 ; i <= n ; i ++ )
        {
            int x, y, l;
            x = read(), y = read(), l = read();
            val[(i << 1) - 1] = y;
            val[i << 1] = y + h - 1;
            Tr[(i << 1) - 1] = (Tree){y, y + h - 1, x , l};     //下底
            Tr[i << 1] = (Tree){y, y + h - 1, x + w - 1, -l};    //上底
        }

        n <<= 1;
        sort(val + 1, val + n + 1);
        sort(Tr + 1, Tr + n + 1);
        int cnt = unique(val + 1, val + n + 1) - val - 1;

        for(register int i = 1 ; i <= n ; i ++ )   //离散化
        {
            int p1 = lower_bound(val + 1, val + cnt + 1, Tr[i].l) - val;
            int p2 = lower_bound(val + 1, val + cnt + 1, Tr[i].r) - val;
            Tr[i].l = p1;                        //记录l和r的排名
            Tr[i].r = p2;
        }

        build(1, 1, cnt);
        int ans = 0;
        for(register int i = 1 ; i <= n ; i ++ )
        {
            modify(1, Tr[i].l, Tr[i].r, Tr[i].val);
            ans = max(ans, tr[1].mx);
        }
        write(ans);
        puts("");
    }

    return 0;
}

★,°:.☆(￣▽￣)/$:.°★ 。完结